Теорема Фалеса. Готові задачі на пропорційні відрізки

Узагальнена теорема Фалеса: паралельні прямі, які перетинають сторони кута, відтинають на його сторонах пропорційні відрізки.
Розглянемо приклади в яких відповідь легко знаходяться завдяки знанням та розумінні теореми Фалеса.
Завдання підібрано із програми ЗНО підготовки з математики.

Задача 44.14 На рисунку AA1=A1A2=A2A3=A3A4  і  A1B1||A2B2||A3B3||A4B4.
Знайти AB2, якщо B1B4=24 см.

Розв'язування: Оскільки відрізки пропорційні AA1=A1A2=A2A3=A3A4 і прямі паралельні A1B1||A2B2||A3B3||A4B4, то за теоремою Фалеса:
AB1=B1B2=B2B3=B3B4.
Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій його стороні.

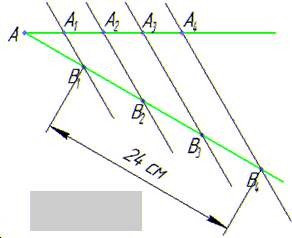
За умовою задачі B1B4=B1B2+B2B3+B3B4=24 см, тобто 3·B1B2=24 см, то звідси маємо AB1=B1B2=B2B3=B3B4=8 см.
Тоді AB2=AB1+B1B2=8+8=16 см.
Відповідь: 16 см –В.

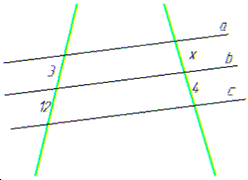
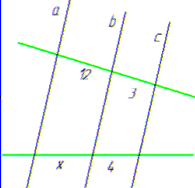
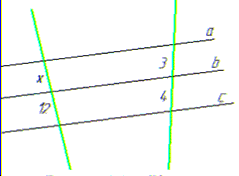
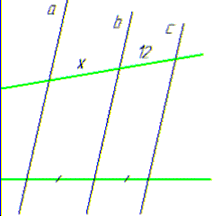
Задача 44.24 Встановити відповідність між рисунками (1–4) та довжинами відрізків x на них, якщо прямі a, b та c – паралельні (А–Д).

А. 12
Б. 9
В. 36
Г. 16
Д. 1

Розв'язування:         Узагальнена теорема Фалеса: паралельні прямі, які перетинають сторони кута, відтинають на його сторонах пропорційні відрізки.
1) 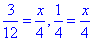,    звідси x=1,     Д;
2) 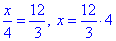,  звідси x=16,     Г;
3) 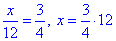,  звідси x=9,       Б;

         Теорема Фалеса: якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій його стороні.

4) x=12,                                          А.

В майбутньому планується сюди добавити ще кілька прикладів, а поки що це все, що було у збірнику із ЗНО підготовки.