«Як знайти рівняння площини, що проходить через три точки?» – саме таке завдання часто підводить студентів. А схема знаходження площини досить проста і зрозуміла.
Перш за все необхідно, щоб точки не лежали на одній прямій. Але цієї умови ніхто не перевіряє, оскільки рідко який викладач задасть завдання на відшукання площини, коли в умові точки із прямої в просторі.
Якщо точки не містяться на одній прямій то вони однозначно визначають площину.
Виведемо формулу площини за відомими 3 точками.
Візьмемо додаткову точку М (х; у;z) з площини і знайдемо вектори, що виходять з однієї точки
М1М3=(x3-x1;y3-y1;z3-z1), М1М =
= (х -x1;y-y1;z-z1),M1М2=
=(х2 - х1; у2 — у1, z2 -z1).
Ці вектори лежать в площині П, тобто вони компланарні. Оскільки мішаний добуток компланарних векторів дорівнює нулю, то маємо векторний запис площини
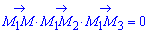
та через координати

Якщо розкласти визначник за алгебраїчними доповненнями до першого рядка, щоб спростити і мати зручний запис, то отримаємо таку формулу площини
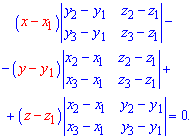
Таким чином, знайшовши визначники другого порядку та звівши подібні доданки, отримаємо загальне рівняння площини
Ax+By+Cz+D=0.
Рівняння площини у відрізках на осях
Будь, яка площина, що проходить через три точки відтинає на осях певні відрізки. Їх досить легко знайти: покладаємо дві координати рівні нулю і знаходимо третю. Зокрема, поклавши y=z=0 загальне рівняння площини набуде вигляду
Ax+D=0
Або
x=a=-D/A.
Так само отримаємо y=b=-D/B; z=c=-D/C.
Отримаємо, що площина відтинає на осях Ох, Оу, Оz відрізки а, b, с, або проходить через точки
А1 (а; 0; 0), В1 (0; b; 0) і С1 (0; 0; с).
Підставляючи координати цих точок у формулу площини і розкриваючи визначник, дістанемо рівняння
хbс + уас + zаb — аbс = 0
або
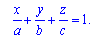
Рівняння називається рівнянням площини у відрізках на осях. Рівняння зручне при побудові площини.
Приклади на складання рівняння площини
Приклад 1. Написати загальне рівняння площини, що проходить через точки М1 (1; -2; 3), М2 (-1; 3; 2), М3 (5; 0; 4).
Розв'язання: Записуємо координати векторів M1M, M1M2, M1M3:
M1M(x-1; y+2; z-3),
M1M2(-1-1; 3+2; 2-3)=(-2; 5; -1),
M1M3(5-1; 0+2; 4-3)=(4; 2; 1).
Складаємо визначник із векторів
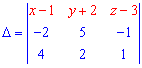
Розписуємо визначник через алгебраїчні доповнення та групуємо подібні доданки
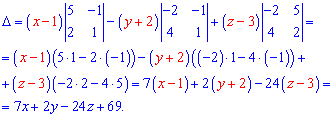
Прирівнявши визначник до нуля, отримаємо шукане рівняння площини
7x+2y-24z+69=0.
Приклад 2. Скласти рівняння площини, яка проходить через точки
М1(1;2;3) , М2(3;5;7), М3(1;2;9) .
Розв'язання: Обчислюємо координати векторів M1M, M1M2, M1M3:
M1M(x-1; y-2; z-3),
M1M2(3-1; 5-2; 7-3)=(2; 3; 4),
M1M3(1-1; 2-2; 9-3)=(0; 0; 6).
Складаємо рівняння площинии через визначник
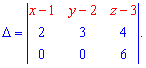
Далі, замість того, щоб розкладати його за елементами першого рядка розкладемо за 3 рядком. Обчислень при цьому стане менше
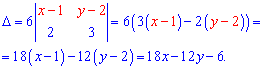
Загальне рівняння площини 18x-12y-6=0 не містить змінної z, а це значить, що z набуває довільних значень, а в площині Oxy маємо пряму 3x-2y-1=0.
Приклад 3. Скласти рівняння площини, яка проходить через 2 точки М1(1;-1;2) , М2(2;5;-3) і перпендикулярна до площини
2х+3у-z+4=0.
Розв'язання: Схема розв'язування задачі наступна:
знаходимо нормальний вектор шуканої площини;
За нормальним вектором і точкою складаємо рівняння площини.
Теоретично все зрозуміло, перейдемо до реалізації.
Нормальний вектор шуканої площини n знаходимо через векторний добуток векторів M1M2 та нормалі l до заданої площини
l(2;3;-1) (2х+3у-z+4=0).
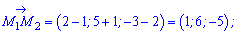
Отже нормаль до шуканої площини має координати n(9; -9; -9).
Знаючи нормальний вектор до площини n(9; -9; -9) і точку на ній М1(1;-1;2), рівняння площини знаходимо за формулою
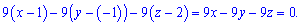
Отримали загальне рівняння площини 9x-9y-9z=0, що не містить вільного доданка. А це значить, що знайдена площина проходить через початок координат.
Рівняння площини в Maple
Для економії часу обчислень можете написати калькулятор на мові програмування чи готовому математичному пакті. Для прикладу, нижче наведено код знаходження рівняння площини в "мейпл" . Це досить простий і потужний математичний пакет, яким можна розв'язати масу задач для інженерів та студентів. В даному прикладі використаємо модуль лінійної алгебри "linalg".
> restart; with(linalg):
Задаємо координати точок через вектори
> M1:=<3,4,7>; M2:=<2,-1,3>; M3:=<4,5,-2>;
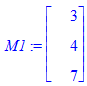
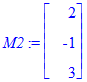
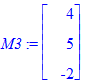
Будуємо три вектори в площині
> M1M:=< x,y,z >-M1;
M1M2:=M2-M1;
M1M3:=M3-M1;
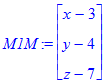
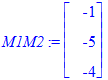
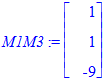
Складаємо з них матрицю
> A:=< M1M|M1M2|M1M3 >;
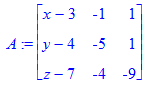
Обчислюємо визначник і прирівнюємо його до нуля.
> Plane:=det(A)=0;
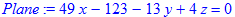
Це і буде рівняння площини, що проходить через три точки. Міняєте координати – отримуєте нове рівняння площини.
На цьому ознайомлення з даною темою завершено. Використовуйте наведені методики у навчанні.


