Продовжуємо аналізувати готові відповіді до завдань із ЗНО підготовки. Сьогодні розв'яжемо приклади, які мають відношення до паралельних прямих та січної. Багато означень та теорем тут наводити не будемо, лише ті, які необхідні для обчислень.
Задача 44.19 На рисунку прямі AB і CD – паралельні.
Знайти градусну міру кута AOC, якщо ∠BAO=300, ∠OCD=500.
А | Б | В | Г | Д |
300 | 500 | 800 | 1000 | визначити неможливо |
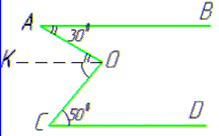
Розв'язування: За умовою задачі AB||CD і ∠BAO=300, ∠OCD=500.
З точки O (вершини кута AOD) проведемо промінь OK так, що AB||OK, OK||CD.
(За теоремою: якщо дві прямі паралельні третій, то вони паралельні між собою).
Тоді отримаємо, ∠AOC=∠AOK+∠KOC (градусна міра кута рівна сумі градусних мір кутів, на які він ділиться будь-яким променем, що проходить між його сторонами).
∠BAO, ∠AOK є внутрішніми різносторонніми кутами при паралельних прямих AB і OK та січній AO, тому за теоремою, ∠AOK=∠BAO=300.
∠KOC, ∠OCD є внутрішніми різносторонніми кутами при паралельних прямих OK і CD та січній OD, тому за теоремою, ∠KOC=∠OCD=500.
Отже, отримаємо ∠AOC=∠AOK+∠KOC=300+500=800.
Відповідь: 800 –В.
Задача 44.23 Встановити відповідність між парами кутів (1–4), зображеними на
рисунку, та їх назвами (А–Д).
1. ∠1 і ∠4 | А. Внутрішні односторонні |
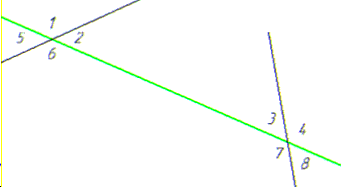
∠1 і ∠4 - зовнішні односторонні кути, Г;
∠6 і ∠8 - відповідні кути, В;
∠7 і ∠7 - внутрішні односторонні кути, А;
∠1 і ∠8 - зовнішні різносторонні кути, Д.
Задача 44.32 Знайти градусну міру кута, під яким січна перетинає паралельні прямі, якщо різниця внутрішніх односторонніх кутів відноситься до їх суми як 2:3.
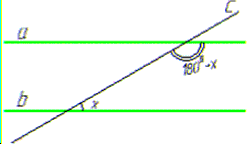
Розв'язування: Маємо паралельні прямі a, b та січну c.
В результаті утворилися внутрішні односторонні кути, сума яких дорівнює 1800 за ознакою паралельністю прямих.
Менший з них позначимо за x, а інший 1800-x.
Їх різниця:
1800-x-x, або 1800-2x.
За умовою задачі, складемо пропорцію, розв'яжемо її, тобто знайдемо x:
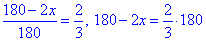
1800-2x=1200, 2x=1800-1200, 2x=600, звідси x=300.
Отже, 300 - градусна міра кута, під яким січна перетинає паралельні прямі.
Відповідь:300.
Задача 44.33 На рисунку прямі AB та CD – паралельні.
Знайти градусну міру кута MOC.
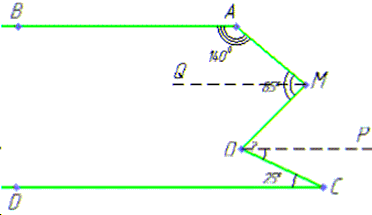
Розв'язування: Властивість кутів, утворених при перетині паралельних прямих січною:
якщо дві паралельні прямі перетнуті третьою прямою, то внутрішні різносторонні кути рівні, а сума внутрішніх односторонніх кутів дорівнює 1800.
За умовою задачі маємо: AB||CD, ∠OCD=25, ∠AMO=85 і ∠BAM=140.
З точок M і O проведемо промені MQ і OP, відповідно, так, що AB||MQ, MQ||OP, OP||CD.
Відрізок AM є січною для паралельних прямих AB і MQ, тоді ∠BAM=140 і ∠AMQ внутрішні односторонні.
За властивістю:
∠BAM+∠AMQ=1800, звідси ∠AMQ=180-∠BAM=1800-1400=400.
За аксіомою вимірювання кутів, отримаємо
∠AMO=∠AMQ+∠OMQ=850, звідси
∠OMQ=∠AMO-∠AMQ=850-400=450.
Відрізок OM є січною для паралельних прямих MQ і OP, тоді ∠OMQ=450 і ∠MOP внутрішні різносторонні.
За властивістю: ∠MOP=∠OMQ=450.
Відрізок OC є січною для паралельних прямих OP і CD, тоді ∠OCD=250 і ∠POC внутрішні різносторонні.
За властивістю: ∠POC=∠OCD=250.
За аксіомою вимірювання кутів, отримаємо
∠MOC=∠MOP+∠POC=45+25=700, отже ∠MOC=700.
Відповідь: 700.
Залишайтеся з нами та отримуйте лише позитив від навчання!


