Вектори називаються компланарними, якщо вони лежать в одній або паралельних площинах.
З цього слідує, що на площині (2D) всі вектори компланарні між собою. Що стосується тримірного простору (3D) то таке твердження не завжди вірне.
В тримірному просторі компланарними будуть кожні два вектори, оскільки через них можна провести паралельні площини.
Якщо маємо більше векторів, то для перевірки використовують необхідну і достатню умову компланарності трьох векторів у просторі.
Умова компланарності векторів
Теорема: Для того, щоб три вектори a,b,c були компланарними необхідно і достатньо, щоб їх мішаний добуток був рівний нулеві.
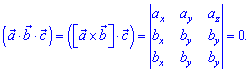
Таким чином, на практиці компланарність перевіряється обчисленням визначника. Якщо визначник рівний 0 – вектори компланарні.
Більший за нуль – вектори утворюють праву трійку.
Менший нуля – вектори утворюють ліву трійку.
Приклади на компланарність векторів
Приклад 1. Перевірити на компланарність вектори
A(1;2;3), B(-3;1;1), C(2;3;5).
Розв'язання: Обчислюємо мішаний добуток векторів
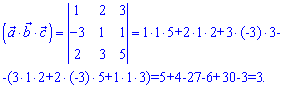
Оскільки мішаний добуток (=3) не рівний нулеві, то вектори не компланарні. Вони утворюють праву трійку.
Приклад 2. Чи будуть компланарними вектори
A(11;2;3), B(-3;1;1), C(5;0;1).
Розв'язання: Знайдемо мішаний добуток векторів
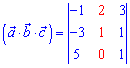
Розкладемо визначник за елементами другого стовпця
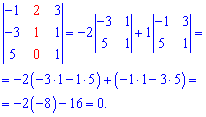
Оскільки мішаний добуток рівний нулю, отже задані вектори компланарні.
Приклад 3. Перевірити, чи належать вектори
AB(1;-1;2), AC(3;2;-1), AD(7;3;0)
одній площині.
Розв'язання: якщо вектори належать площині, то вони за означенням компланарні. Знайдемо мішаний добуток векторів і перевіримо, чи він рівний нулю.
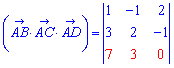
Розкладемо визначник за елементами третього рядка
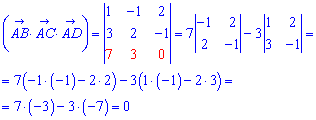
Умова рівності нулю мішаного добутку виконується, отже вектори компланарні.
Приклад 4. Перевірити, чи належать точки
A(4; 1; -1), B(2; 2; 3), C(-8;-2;5) , D(-3; -1; 2)
одній площині.
Розв'язання: Побудуємо вектори, що починаються в точці A.
AB(2-4; 2-1; 3+1)=(-2; 1; 4);
AC(-8-4; -2-1; 5+1)=(-12; -3; 6);
AD(-3-4; -1-1; 2+1)=(-7; -2; 3).
Обчислюємо мішаний добуток знайдених векторів
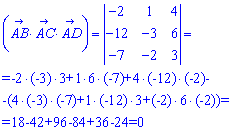
Визначник рівний нулю, отже точки належать одній площині.
Перевірка на компланарність векторів в Maple
Якщо завдання виконуєте вдома, а не на заняттях, то можете використовувати математичні пакети. Їх досить багато і з допомогою інтернету можна вивчити будь-яку. Я в свій час навчався працювати в Maple, тому залюбки поділюся з Вами досвідом. Код програми для останнього прикладу наступний
> restart;
> with(linalg): підключаємо модуль лінійної алгебри
> AB:=<-2,1,4>; AC:=<-12,-3,6>; AD:=<-7,-2,3>; - вводимо вектори.
> A:=< AB|AC|AD >; - формуємо матрицю
> ABC:=det(A); обчислюємо мішаний добуток векторів
В результаті отримаємо наступний результат
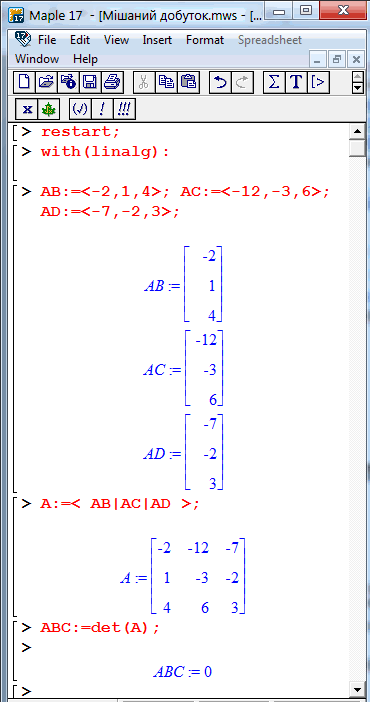
Якщо не маєте бажання вивчати "МЕЙПЛ" чи другі математичні пакети, то можете завантажити математичний калькулятор YukhymCalc з цього сайту.
В меню вибираєте визначник матриці
Вводите вектори мішаного добутку
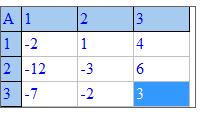
і отримуєте результати обчислень

Якщо мішаний добуток (визначник) рівний нулю – вектори компланарні. В протилежному випадку вектори не компланарні.
Використовуйте калькулятор для обчислення визначника та наведений алгоритм перевірки компланарності векторів.


