Готові розв'язки до неоднорідних диференціальних рівнянь, права частина яких має вигляд експоненти, синус та косинус функцій або добутку експоненти на ці функції будуть проаналізовані в цій публікації. Теоретичний матеріал достатьо важкий для розуміння, тому його тут приводити не будемо. Завдання взято з контрольної роботи, яку задавали у Львівському національному університеті ім. І.Франка. Хто там навчається на математичних дисциплінах можливо знайде серед наведених відповідей свій варіант. Усі решта отримають добрий алгоритм знаходження розв'язку складних неоднорідних диференціальньних рівнянь такого типу.
Приклад 1. (12.4) Знайти загальний розв'язок диференціального рівняння:
Розв'язання: Задано неоднорідне диференціальне рівняння (ДР) другого порядку, права частина якого містить як експоненту, так і тригонометричні функції. Для всіх неоднорідних рівнянь розв'язок представляємо у вигляді суми інтегралу однорідного ДР та часткового розв'язку неоднорідного 
. Це важиво знати і ми кожного уроку Вам нагадуємо.
Оскільки з однорідними рівняннями, як правило, в більшості студентів проблем не виникає, то наведені ДР лякають усіх якраз правою стороною. Добре запам'ятайте наведену далі схему розв'язання ДР, вона спільна для усіх неоднорідних ДР.
Усі обчислення починаються з однорідного диференціального рівняння
для нього інтеграл шукаємо у вигляді суми експоненціальних функцій y=exp(k*x). При підстановці в однорідне ДР отримаємо характеристичне рівняння
На експоненту, яка мала би бути присутньою завжди скорочують, оскільки вона додатна для всіх можливих значень аргументу. З неповного квадратного рівняння знаходимо 2 комплексні корені 
Далі аналізуємо їх значення. Оскільки корені характеристичного рівняння є комплексно спряженими і не містять дійсної частини, то розв'язок однорідного рівняння рівний сумі сталих помножених на косинус та синус функції відповідних аргументів
Цей перехід запам'ятайте, оскільки на цьому моменті погано роблять наголос в теорії, а потім на практиці мало хто з Вас може пояснити, чому розв'язок шукали у вигляді експоненти, а у відповідь без всяких пояснень записують косинус та синус функції.
Повернемося до обчислень та розглянемо неоднорідну частину рівняння. Оскільки функція в правій частині
подібна до розв'язку однорідного ДР синусом та косинусом (тобто множники при "ікс" є коренями характеристичного рівняння) то частковий розв'язок шукаємо у вигляді
Якщо б неоднорідна частина мала синуси та косинуси з відмінними від характеристичного рівняння коренями (аргументами), то дужки, що містять косинус і синус в частковому розв'язку домножати на "ікс" не потрібно (буде розглянуто далі).
Для визначення трьох сталих A, B, D підставимо "ігрик" в початкове диференціальне рівняння, попередньо обчисливши першу та другу похідні
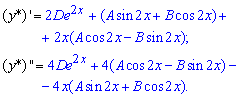
Після групування подібних доданків, отримаємо залежність для встановлення невідомих констант A, B, D
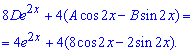
Прирівнявши множники при sin(2x), cos(2x), exp(2x), отримаємо систему 3 лінійних рівнянь з трьома невідомими
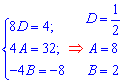
розв'язуючи яку знаходимо сталі D=0,5; A=8; B=2.
Отож, ми знайшли частковий розв'язок неоднорідного диференціального рівняння
.
Загальний розв'язок ДР обчислюємо за формулою
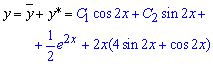
де С1, С2 - довільні константи. На цьому і базується методика обчислення неоднорідних ДР такого вигляду, розглянемо іші варіанти, які Ви можете зустріти на контрольних, тестах, модулях.
Приклад 2. (12.14) Знайти загальний розв'язок диференціального рівняння:
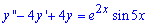
Розв'язання: Загальний інтеграл неоднорідного диференціального рівняння другого порядку шукаємо через суму двох функцій.
Для однорідного ДР складаємо характеристичне рівняння і знаходимо його розв'язки
Отримані значення є кратними, тому загальний інтеграл однорідного ДР записуємо у вигляді
Якщо наприклад, маємо ДР третього порядку і три корені характеристичного рівняння кратні то в дужках буде третій доданок у вигляді константи на аргумент в квадраті +C3x2, для четвертого кратного добавиться +C4x3 і так далі.
Аналізуємо неоднорідну частину ДР - вона містить експоненту помножену на синус функцію, тому частковий розв'язок шукаємо у вигляді
Косинус слід включати, оскільки перша похідна від нього дасть синус, який може внести свій вклад в результат. Знайдемо константи А, В: для цього підставимо функцію в задане диференціальне рівняння і прирівняємо коефіцієнти при sin(5x), cos(5x)
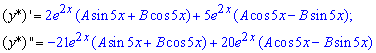
Після підстановки похідних в ДР і сумування подібних доданків отримаємо залежність
Прирівнюючи множники при синусах і косинусах, знаходимо шукані сталі
Частковий розв'язок з урахуванням A, B прийме вигляд
Щоб записати формулу загального розв'язку диференціального рівняння до знайденої функції додаємо інтеграл однорідного рівняння
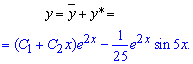
У випадку задачі Коші сталі C1, C2 знаходимо з умови рівності функції та її похідної певним значенням в початковій точці
Звідси маємо два рівняння для визначення двох констант.
Приклад 3.(12.17) Знайти загальний розв'язок диференціального рівняння:
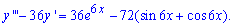
Розв'язання: Розв'язок неоднорідного диференціального рівняння третього порядку шукаємо через суму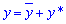 
. Для однорідного рівняння характеристичне рівняння і корені рівні
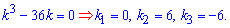
Оскільки всі значення різні та дійсні, то розв'язок записуємо у вигляді
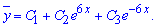
Відповідно до правої сторони частковий розв'язок ДР шукаємо у вигляді
Обчислюємо першу-третю похідні від функції
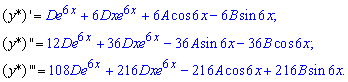
та підставляємо у рівняння. Після групування доданків Ви повинні отримати наступну залежність
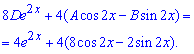
Невідомі коефіцієнти A, B, D знаходимо прирівнявши коефіцієнти при
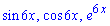
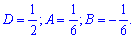
Отож, формула часткового розв'язку диференціального рівняння наступна
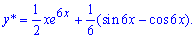
Повний розв'язок диференціального рівняння знаходимо за формулою
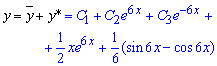
де С1, С2, С3 – будь-які константи.
Приклад 4. (12.22) Знайти загальний розв'язок диференціального рівняння:
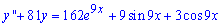
Розв'язання: Маємо неоднорідне диференціальне рівняння другого порядку. Розв'язок згідно методики обчислень неоднорідних рівнянь розбиваємо на суму двох .
Спершу розглядаємо однорідне рівняння, для нього складаємо характеристичне рівняння і знаходимо корені
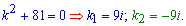
При обчисленні неповного квадратного рівняння отримали два комплексно спряжені числа, які не мають дійсної частини. В таких випадках загальний інтеграл однорідного ДР виражається через синус і косинус функції
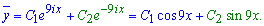
Далі аналізуємо неоднорідну складову рівняння. Тригонометрична її частина має подібний до однорідного розв'язку склад аргументів функцій, тому в частковому розв'язку це виражається до множенням синуса та косинуса на "ікс"
Знайдемо коефіцієнти A, B, D: для цього підставимо цей вираз в початкове диференціальне рівняння і прирівняємо коефіцієнти при sin(9x), cos(9x) і e9x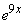
.
Обчислюємо другу похідну функції
Підставляючи в ДР, і спрощуючи вирази, отримаємо
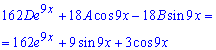
Звідси отримаємо сталі D=1, A=1/6 і B=-1/2.
Частковий розв'язок при підстановці констант прийме вигляд
.
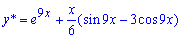Загальний інтеграл неоднорідного диференціального рівняння обчислюємо за формулою
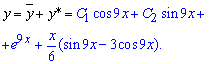
де C1 і C2 - довільні константи.
Їх можна уточнити, якщо поряд із ДР задана умова Коші.
Тут таких завдань не розглядаємо, хоча вони достатньо прості. Вивчайте правила обчислення похідних та інтегрування, без цього неможливо навчитися швидко вирішувати диф. рівняння.
На цьому завершуються пояснення до контрольної роботи з диференціальних рівнянь. Більше готових прикладів та інструкцій в наступних матеріалах.
