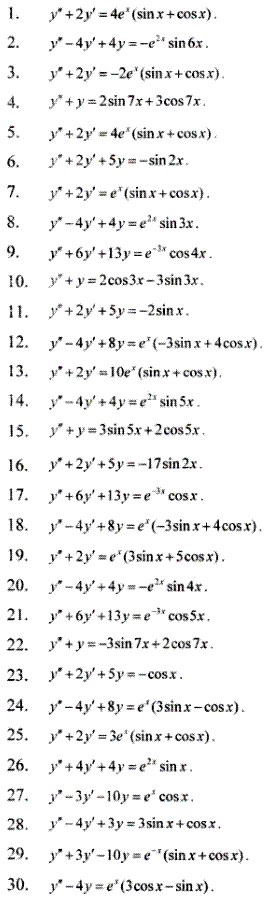На попередньому занятті ми розібрали неоднорідні диференціальні рівняння 3,4 порядку, що в нелінійній частині містили множником експоненту. З цього уроку Ви навчитеся обчислювати неоднорідні ДР, що містять в правій частині тригонометричні функції - синус та косинус. Також розглянемо випадки, коли неоднорідна частина ДР має вигляд добутку експоненти на синус та косинус. Забігаючи вперед можу лише підказати, що це все пов'язано з експонентою, а саме з комплексними показниками експоненти. Якщо проаналізуєте статтю до кінця, то будете знати "Як знайти розв'язок неоднорідного диференціального рівняння з комплексними коренями характеристичного рівняння?". І це ще не складні завдання, наступні уроки міститимуть куди важчі приклади.
Приклад 1. (11.4) Знайти загальний розв'язок диференціального рівняння
![]()
Розв'язання: Розв'язок неоднорідного диференціального рівняння другого порядку шукаємо у вигляді суми кореня однорідного рівняння та часткового розв'язку неоднорідного рівняння 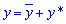
Для однорідного диф. р-ня (ДР) розв'язок шукаємо у вигляді експоненціальної функції y=exp(k*x). При підстановці у рівняння і спрощенні не експоненту отримаємо наступне характеристичне рівняння
![]()
Його корені комплексно спряжені, тому інтегралом однорідного рівняння буде комбінація синус та косинус функції
![]()
Далі приступаємо до відшукання часткового розв'язку неоднорідного ДР. Відповідно до правої сторони вихідного рівняння розв'язок шукаємо у вигляді
![]()
Обчислюємо другу похідну, що міститься у рівнянні
![]()
Далі підставляємо знайдену похідну та значення функції в початкове рівняння
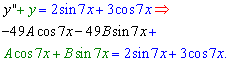
Прирівнюючи множники при синусу та косинусу отримаємо залежності, з яких обчислюємо сталі
![]()
Записуємо частковий розв'язок диференціального рівняння, попередньо звівши доданки під спільний знаменник
![]()
Ну і не забуваємо все підставити у формулу загального розв'язку диференціального рівняння
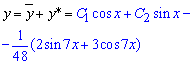
тут С1, С2 -сталі, що приймають довільні значення.
Приклад 3,4*. Знайти загальний розв'язок лінійного неоднорідного диференціального рівняння другого порядку зі сталими коефіцієнтами.
3 4y''-y=x^3-24x. Маємо неоднорідне диференціальне рівняння зі сталими коефіцієнтами, розв'язок якого будемо шукати у вигляді:

Розв'яжемо відповідне однорідне рівняння:
4y''-y=0.
Складаємо відповідне характеристичне рівняння і шукаємо його корені: 4k2-1=0,
звідси (за теоремою Вієта)
k1=k2=1/2.
Отож загальний розв'язок однорідного диференціального рівняння має вигляд:
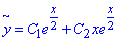
Знайдемо частковий розв'язок заданого диференціального рівняння. Права частина містить вираз x3-24x, тому його розв'язок будемо шукати у вигляді:
y*=Ax^3+bx^2+Dx+E.
Знайдемо похідні І та ІІ порядку функції y* по змінній x: (y*)'=3Ax^2+2B•x+D,
(y*)''=6Ax+2B.
Підставимо y*, (y*)'' у задане диференціальне рівняння:
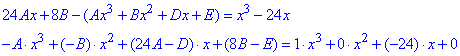
Прирівняємо коефіцієнти при однакових множниках у двох частинах рівності та з системи рівнянь визначимо невідомі:
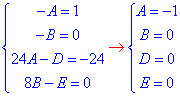
Запишемо частковий розв'язок заданого диференціального рівняння:
y*=-x3.
Запишемо розв'язок диференціального рівняння:
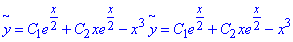
де C1, C2 – довільні сталі.
4. y''+2y'+5y=4sin(x).
Маємо неоднорідне диференціальне рівняння зі сталими коефіцієнтами, розв'язок якого будемо шукати у вигляді:

Розв'яжемо відповідне однорідне рівняння:
y''+2y'+5y=0.
Складаємо відповідне характеристичне рівняння і знаходимо його корені:
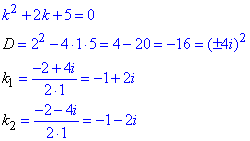
Загальний розв'язок однорідного ДР має вигляд:
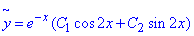
Знайдемо частковий розв'язок диференціального рівняння. Права частина містить вираз 4sin(x), причому число і не є коренем характеристичного рівняння, тому його розв'язок будемо шукати у вигляді:
y*=A•cos(x)+B•sin(x).
Знайдемо похідні І та ІІ порядку функції y* за змінною x:
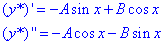
Підставимо y*, (y*)', (y*)'' у задане диференціальне рівняння:
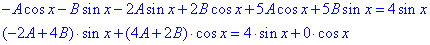
Прирівняємо коефіцієнти при однакових множниках у двох частинах рівності:
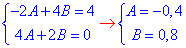
Підставимо А,В в частковий розв'язок заданого диференціального рівняння:
y*=-0,4cos(x)+0,8sin(x).
Запишемо розв'язок ДР:
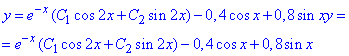
де C1, C2 – довільні сталі.
Приклад 5*. Знайти частинний розв'язок лінійного неоднорідного диференціального рівняння другого порядку зі сталими коефіцієнтами.
y''+6y'+9y=9xe^-3x, y(0)=2, y'(0)=1.
Обчислення: Маємо неоднорідне диференціальне рівняння зі сталими коефіцієнтами, тому його розв'язок шукаємо у вигляді суми двох:

Розв'яжемо відповідне однорідне рівняння:
y''+6y'+9y=0.
Складаємо відповідне характеристичне рівняння і шукаємо його корені:
k2+6k+9=0, або (k+3)2=0, звідси k1=k2=-3.
Загальний розв'язок однорідного диференціального рівняння має вигляд:
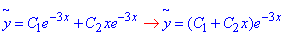
Знайдемо частковий розв'язок заданого диференціального рівняння. Права частина містить вираз 9xe-3x, причому число -3 є 2-х кратним коренем характеристичного рівняння, тому його розв'язок будемо шукати у вигляді:
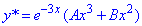
(В дужках стоїть многочлен другого порядку з невизначеними коефіцієнтами A, B, оскільки в правій частині заданого рівняння є саме такий многочлен). Знайдемо похідні І та ІІ порядку функції y* по змінній x (і зразу зведемо подібні доданки):
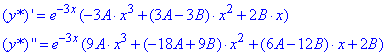
Підставимо y*, (y*)', (y*)'' у задане диференціальне рівняння (і зразу зведемо подібні доданки):
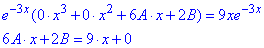
Прирівняємо коефіцієнти при однакових множниках у двох частинах рівності:
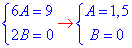
Отож, запишемо частковий розв'язок заданого диференціального рівняння:
y*=1,5x3e-3x.
Запишемо загальний розв'язок заданого диференціального рівняння ():
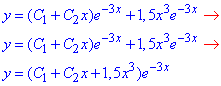
де C1, C2 – довільні сталі.
Розв'яжемо задачу Коші, для цього підставимо початкові умови
y(0)=2, y'(0)=1
у загальний розв'язок ДР:
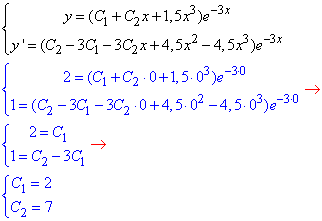
Підставляємо їх в y=(2+7x+1,5x3)e-3x - частинний розв'язок рівняння.
Приклад 2. (11.7) Розв'язати диференціальне рівняння
![]()
Розв'язання: Маємо неоднорідне диференціальне рівняння другого порядку, причому права сторона містить експоненту помножену на суму косинус і синус функцій. Розв'язок неоднорідних рівнянь завжди шукаємо у вигляді суми двох 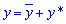 .
.
Спершу обчислюємо однорідне диференціальне рівняння, для цього складаємо характеристичне рівняння ![]() і знаходимо корені
і знаходимо корені ![]()
Оскільки коефіцієнти характеристичного рівняння є різними дійсними числами, то інтеграл однорідного ДР матиме вигляд суми сталих помножених на експоненти у відповідних степенях
![]()
Оскільки неоднорідна частина ДР =ex(sin(x)+cos(x) не містить експоненти в степені кореня характеристичного рівняння (0;-2), то частковий розв'язок має простий вигляд
![]()
Знайдемо коефіцієнти A і B - для цього підставимо цей вираз у диференціальне рівняння і прирівняємо множнии при sin(x) і cos(x):
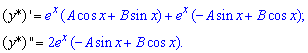
Після підставлення похідних та спрощень, отримаємо
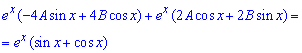
Прирівнюючи значення при sin(x), cos(x), отримаємо систему рівнянь відносно сталих А, B
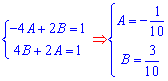
Її не важко розв'язати, оскільки маємо всього два рівняння і дві невідомі. Знайдені значення підставляємо у формулу часткового розв'язку неоднорідного ДР
![]()
Загальний розв'язок диференціального рівняння рівний сумі знайдених функцій
![]()
де C1, C2 - довільні константи.
Приклад 3.(11.17) Знайти загальний інтеграл диференціального рівняння
![]()
Розв'язання: Розв'язок неоднорідного диф. рівняння шукаємо за класичною схемою. Для однорідного рівняння 2 порядку записуємо характеристичне рівняння і розв'язуємо його
![]()
Отримали комплексно спряжені корені характеристичного рівняння. Це новий тип ДР, тому запам'ятайте, що інтеграл однорідного диференціального рівняння в таких випадках виражається через добуток експоненти на синус та косинус функції.
![]()
Зауважте, що дійсна частина характеристичного числа є показником експоненти, а уявні значення фігурують в якості аргументів косинус та синус функцій. Запам'ятайте це, бо подібні характеристичні корені поширені в такого роду ДР.
Проаналізуємо тепер, як шукати інтеграл неоднорідного ДР. Щоб при диференціюванні отримати праву частину рівняння e-3xcos(x) частковий розв'язок потрібно шукати у вигляді
![]()
Знаходимо першу та другу похідні функції
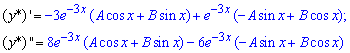
та підставляємо у початкове диф. рівняння. Після усіх спрощень Ви повинні отримати вираз
![]()
З множників при косинусі та синусі формуємо залежності для встановлення констант A=1/3; B=0.
Таким чином отримаємо частковий розв'язок диференціального рівняння
![]()
Щоб записати загальний розв'язок диференціального рівняння до знайденого додаємо корінь однорідного рівняння
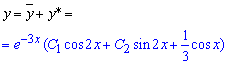
Приклад 4. Знайти загальний розв'язок лінійного неоднорідного диференціального рівняння другого порядку зі сталими коефіцієнтами методом невизначених коефіцієнтів.
5 y''+3y'+2y=4x+12.
Обчислення: Маємо неоднорідне диференціальне рівняння зі сталими коефіцієнтами, розв'язок якого будемо шукати у вигляді:

Розв'яжемо відповідне однорідне рівняння:
y''+3y'+2y=0.
Складаємо відповідне характеристичне рівняння і шукаємо його корені: k^2+3k+2=0,
звідси k1=-2, k2=-1.
Підставляємо в загальний розв'язок однорідного диференціального рівняння:
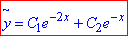
Знайдемо частковий розв'язок ДР.
Права частина містить вираз 4x+12, причому число 0 не є коренем характеристичного рівняння, тому його розв'язок будемо шукати у вигляді:
y*=Ax+B.
Знайдемо похідні І та ІІ порядку функції y* за змінною x:
(y*)'=A,
(y*)''=0.
Підставимо y*, (y*)' і (y*)'' у задане диференціальне рівняння: 0+3A+2Ax+2B=4x+12,
2A•x+(3A+2B)=4•x+12.
Прирівняємо коефіцієнти при однакових множниках у двох частинах рівності:
{2A=4, 3A+2B=12},
звідси отримаємо A=2, B=3.
Складемо частковий розв'язок ДР:
y*=2x+3.
Запишемо розв'язок заданого в умові ДР:
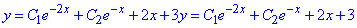
де C1 і C2 – довільні сталі.
На цьому і ґрунтується розв'язання всіх ДР такого сорту. Алгоритм обчислень Вам тепер знайомий, як розв'язати неоднорідне диференціальне рівняння наведеного вигляду теж тепер знаєте. Тож для закріплення матеріалу пропонуємо розв'язати самостійно декілька з наступних ДР