Однорідні диференціальні рівняння є частковим випадком неоднорідних при відсутній правій частині. Тому їх алгоритм обчислень один в один повторюється і тут на ньому наголошувати не будемо. Розберемо кілька завдань для рівнянь зі сталими коефіцієнтами, щоб Ви побачили в якому вигляді шукати розв'язок ДР.
Приклад 1. Знайти загальний розв'язок лінійного однорідного диференціального рівняння другого порядку зі сталими коефіцієнтами.
а) y''-4y'+13y=0.
Обчислення: Розв'яжемо відповідне характеристичне (алгебраїчне) рівняння, ввівши заміну:
y(n)->k(n), де
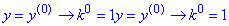
(Тобто порядок похідної функції y вказує на степінь змінної k).
Корені характеристичного рівняння обчислюємо через дискримінант
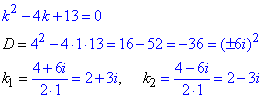
Оскільки корені є комплексними числами (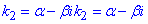 
), то розв'язок заданого диференціального рівняння записуємо у вигляді: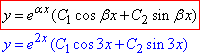 
де C1 і C2 – довільні сталі.
б) y''+3y'-28y=0
Обчислення: Розв'яжемо відповідне характеристичне (алгебраїчне) рівняння, ввівши заміну:
y(n)->k(n) , де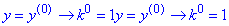 
(Порядок похідної функції y вказує на степінь змінної k). Отже,
Через дискримінант отримаємо два різні корені
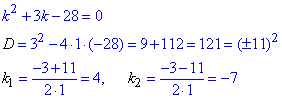
Оскільки корені характеристичного рівняння є різні дійсні числа (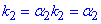
), то розв'язок заданого диференціального рівняння записуємо у вигляді:
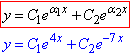
де C1 і C2 – довільні сталі.
в) Знайти частинний розв'язок лінійного однорідного диференціального рівняння другого порядку зі сталими коефіцієнтами.
36y''-60y'+25y=0, y(0)=5/6, y'(0)=25/36.
Обчислення:Складемо та обчислимо відповідне характеристичне (алгебраїчне) рівняння.
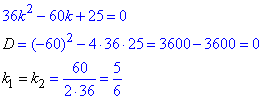
Бачимо, що корені характеристичного рівняння є однакові дійсні числа (k1=k2=α), тому загальний розв'язок диференціального рівняння записуємо у вигляді:
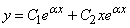, тобто
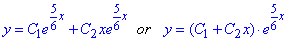
де C1, C2 – довільні сталі, які уточнюємо з умови Коші:
Підставимо початкові умови y(0)=5/6, y'(0)=25/36 у загальний розв'язок ДР:
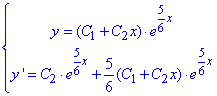
отримаємо
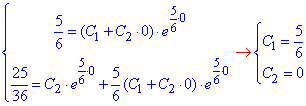
Підставлямо С1=5/6, С2=0 в "ігрик", звідси
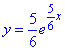- частинний розв'язок рівняння.
Тут розібрали варіанти, які найчастіше Вам задають на практичних. Більше готових відповідей на ДР можна переглянути на сусідніх сторінках сайту.
