В головній публікації практикуму з аналітичної геометрії наведено задачі з визначення, що собою являє поверхня другого порядку та знаходження центру поверхні. В цій та наступних публікаціях наведено аналіз більшої кількості прикладів з поясненням можливих схем їх обчислень. Що краще та швидше вибирати повинні Ви, тому перегляньте завдання та оберіть свій алгоритм їх вирішення.
Задач на визначення типу поверхні
Задача 6.2.1 Визначте тип поверхні другого порядку:
б) x2-y2+3z2-6x+6z+3=0.
Розв'язання: Доповнюємо рівняння та виділяємо повні квадрати
x2-6x+9-y2+3z2+6z+3-9-3+3=0;
(x-3)2-y2+3(z+1)2=32.
Залишилося знормувати отриману залежність на праву частину від знаку рівності і отримаємо
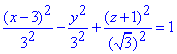
однополий гіперболоїд (витягнутий вздовж осі Oy) з центром O(3;0;-1) і півосями 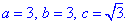
Чому саме такий гіперболоїд - проаналізуйте кінцеве рівняння та співставте висновки, або ж заново беріться за теорію поверхонь дргого порядку.
Задача в) З'ясувати тип поверхні другого порядку:
x2-z2-2x+6z-8=0.
Розв'язання: Перегруповуємо доданки та виділяємо повні квадрати
x2-2x+1-z2+6z-9-1+9-8=0;
(x-1)2-(z-3)2=0.
Далі до рівняння застосовуємо формулу різниці квадратів
(x-1+z-3)(x-1-z+3)=0;
(x+z+4)(x-z+2)=0.
Таким чином початкова залежність розщеплються на два рівняння площини
x+z+4=0;
x-z+2=0,
що перетинаються по дійсній прямій.
Це і є шуканий тип поверхні. У всіх випадках, коли в початковій формулі замасковано рівняння площин схема перетворень буде ідентична, то ж просто один раз її вивчіть.
Задача г) Яка поверхня задана рівнянням:
x2+2y2+3z2-6z+3=0.
Розв'язання: Зведемо до канонічного вигляду дане рівняння, для цього виділимо повний квадрат при "z".
x2+2y2+3z2-6z+3-3+3=0;
x2+2y2+3(z-1)2=0.
На цьому у багатьох студентів перетворення заходять в глухий кут. Але це не правильно, потрібно множники при змінних загнати в знаменник. Для цього 2 і 3 представимо як 1/2, 1/3 в знаменнику, при цьому останнє рівняння набуде вигляду

Отримали уявний конус.
Задача д) Звести до канонічного вигляду поверхню другого порядку:
xy+3z2-18z+54=0.
Розв'язання: Маємо новий тип рівнянь, який за попередньою методикою звести до повних квадратів не вдасться. Зведемо поверхню другого порядку до канонічного вигляду методом Лагранжа.
Суть методу полягає в заміні змінних:

При цьому неважливо в якому порядку позначатимемо змінні, тобто варіант
x=x'-y';
y=x'+y'
також приведе до правильного кінцевого рівняння.
Нові змінні підставляємо в початкову рівняння поверхні другого порядку
(x'+y')(x'-y')+(3z')2-18z'+54=0.
Вже з цього запису Ви можете бачити, для чого застосовували заміну змінних?
Вона дозволяє від добутку змінних перейти до різниці квадратів нових змінних, а рівняння поверхні другого порядку при цьому перетвориться до вигляду
(x')2-(y')2+(3z')2-18z'+27-27+54=0.
Тут додали та відняли 27, щоб виділити повний квадрат при змінній z'.
Рівняння набуде вигляду
(x')2-(y')2+3(z'-3)2-18z'=-27.
Далі нормуємо обидві частини на 27, та зносимо трійку при (z'-3) в знаменник.
В результаті

отримали канонічне рівняння двополого гіперболоїда.
Рівняння двополого гіперболоїда в системі координат Oxy має вигляд:
xy+3(z-3)2=-27.
Якщо Ви зрозуміли наведений алгоритм, то вважайте, що ще одна частина задач на рівняння поверхні другого порядку Вам під силу.
Для закріплення отриманих знань розглянемо подібні рівняння поверхонь.
Задача е) Визначте тип поверхні другого порядку:
xz-6z+3=0.
Розв'язання: Як і в попередньому приладі, при зведенні до канонічного вигляду застосовуємо метод Лагранжа.
Для цього зробимо заміну змінних:

Перепишемо рівняння поверхні
(x'+z')(x'-z')-6(x'-z')+3=0.
Отримали різницю квадратів
(x')2-(z')2-6x'+6z'+3=0;
(x')2-6x'+9-(z')2+6z'-9+3=0;
(x'-3)2-(z'-3)2=-3.
При нормуванні рівняння поверхні на (-3) отримаємо

канонічне рівняння гіперболічного циліндра.
Повторна заміна змінних

дає запис

який є канонічним рівняння гіперболічного циліндра в канонічній системі координат
Гіперболічний циліндр в декартовій системі координат Oxy матиме вигляд:
(x-6)z=-3,
його вісь паралельна осі Oy.
Задача є)Звести до канонічного вигляду поверхню:
yz+4x-6y+12z+25=0.
Розв'язання: З вигляду поверхні робимо висновок, що потрібно застосувати метод Лагранжа.
Заміна змінних вперед:

та назад
 (*)
(*)
Тоді вихідне рівняння перетворимо до наступного
(y'+z')(y'-z')=4x'-6(y'+z')+12(y'-z')+25=0;
(y')2-(z')2+4x'-6y'-6z'+12y'-12z'+25=0.
Далі доповнюємо квадратичні залежності до повних квадратів
(y')2-6y'+9-(z')2-18z'-81-9+81+4x'+25=0;
(y'+3)2-(z'+9)2=-4(x'+24,5).(**)
Незвичне рівняння, яке ще потрібно перетворювати.
Для цього робимо заміну:

Зворотній перехід, враховуючи (*) буде мати вигляд

Тоді рівняння поверхні (**) зведеться до
(y'')2-(z'')2=-4x''.
канонічного рівняння гіперболічного параболоїда в канонічній системі координат.
Задача ж) Який тип має поверхня другого порядку?
x2+4xz-4z2-6z+3=0.
Розв'язання: Тут можна застосовувати метод Лагранжа, а можна обійтись і без нього. Для цього перші два доданки доповнимо до повного квадрату і те ж саме виконаємо з частиною рівняння поверхні, що залишиться.
В результаті математичних перетворень матимемо

Такий запис легко читати, проте ще одна заміна змінних

перетворює рівняння поверхні до

канонічного рівняння гіперболічного циліндра.
Цих завдань цілком вистачає, щоб навчитися обчислювати завдання подібного типу.
Більше прикладів на зведення поверхні другого порядку до канонічного вигляду та з'ясування її типу в наступній публікації.


