Дослідження поверхонь другого порядку пов'язано з обчисленням систем лінійних рівнянь, диференціюванням, заміною змінних, і без знання всього цього Ви не завжди зможете знайти правильну відповідь.
Наведені нижче приклади задавали в ЛНУ ім. І. Франка, механіко-математичний факультет, кафедра геометрії і топології
ПРАКТИКУМ з аналітичної геометрії
Розділ VI: «Поверхні другого порядку».
Частина IІ: «Загальна теорія поверхонь другого порядку».
Частина IІІ: «Центр поверхні другого порядку».
Поверхнею другого порядку (ПДП) називається множина точок простору, координати яких в деякій афінній системі координат задовольняють рівняння другого порядку
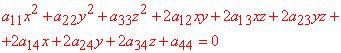 (1)
(1)
причому хоча б один з коефіцієнтів при подвійних добутках змінних відмінний від нуля
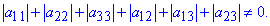
Приймаємо, що aij=aji, тобто матриця складена з коефіцієнтів рівняння симетрична. Точка S називається центром поверхні другого порядку, якщо разом з довільною точкою М цієї поверхні їй належить і точка M', симетрична до точки M стосовно точки S.
Точка S є центром поверхні (2) тоді і лише тоді, коли її координати задовольняють систему рівнянь:
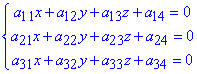
(або в 1, 2 і 3 рівнянні необхідно взяти частинну похідну по змінній x, y, z відповідно).
Задачі на поверхні другого порядку
Задача 6.2.1 Визначте тип поверхні другого порядку:
а) x2+y2+z2-12x+4y-6z+24=0.
Розв'язання: Схема обчислень одна і та ж для всіх завдань з такою умовою, тому уважно прослідкуйте за наступними перетвореннями.
Зведемо рівняння поверхні другого порядку до канонічного вигляду методом виділення повних квадратів:
x2-12x+36+y2+4y+4+z2-6z+9-36-4-9+24=0.
Як доповнювати квадратичну форму до повного порядку Ви повинні знати, якщо ні уважно слідкуйте як ми перетворюємо формули і за кілька занять опануєте методику. В результаті прийдемо до рівняння
(x-6)2+(y+2)2+(z-3)2=52.
Тут опущені сумування вільного члена, проте в правильності можете переконатися самостійно.
Отримали рівняння сфери з центром O(6;-2;3) і радіусом R=5.
Задача 6.2.2 Визначте тип поверхні другого порядку:
а) 4x2-2y2-12z2+4xy+12yz=0;
Розв'язання: Ви повинні знати, що на практиці Вам не зададуть завдань, які важко вирішити. Тож в більшості випадків поверхню другого порядку потрібно зводити до канонічного вигляду методом виділення повних квадратів. Підказкою служать коефіцієнти, наприклад маємо
4x2+4xy.
До повного квадрату (2x+y)2 тут не вистачає y2.
Отож додаємо та віднімаємо y2, щоб отримати повний квадрат і, одночасно, не змінити рівняння поверхні.
І так само аналізуємо решту частини рівняння.
В результаті отримаємо наступні перетворення
4x2+4xy+y2-3y2+12yz-12z2=0;
(2x+y)2-3(y-2z)2=0.
Оскільки права частина рівняння рівна нулю, то маємо формулу різниці квадратів, яку можемо записати через добуток

Отримали дві дійсні площини

що перетинаються по дійсній прямій.
Це і є шуканим типом поверхні.
Пояснення, думаю, зрозумілі всім, тому переходимо до інших завдань, тим більше що їх тут ще багато.
Задача 6.3.1 Знайдіть центр поверхні другого порядку:
а) 2x2-y2+z2-4x+4z+3=0.
Розв'язання: Випишемо коефіцієнти рівняння заданої поверхні другого порядку:
a11=2, a22=-1, a33=1, a12=0, a13=0,a23=0,a14=-2, a24=0,a34=2,a44=3.
Знайдемо центр поверхні другого порядку (ПДП), для цього складаємо систему з трьох лінійних рівнянь та обчислюємо її:
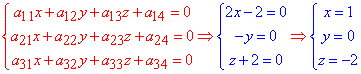
Точка з координатами O(1;0;-2) є центром заданої поверхні другого порядку.
З розрахунків Ви бачите, що основною задачею тут є правильно та швидко розв'язати систему лінійних рівнянь. Щоб її отримати потрібно без помилок виписати коефіцієнти при квадратичній формі запису поверхні, що теж не є важко. Всі необхідні формули Вам відомі, тож ваші результати на практиці залежать лише від знань цих формул.
Задача 6.3.2 Перенесіть початок координат в центр поверхні другого порядку:
а) x2+2y2+2z2+2xy-2x-4y-4z=0;
Розв'язання: Завдання дещо складніше від попередніх, оскільки щоб перенести початок координат в центр поверхні спершу необхідно цей центр знайти. Крім цього потрібно зробити заміну координат, що автоматом потягне за собою перетворення поверхні. Тут є багато місць де можна допустити помилку, тож уважно обчислюйте та не спішіть. Уважно розгляньте універсальний алгоритм для такого виду завдань.
Зведемо спершу рівняння поверхні другого порядку до канонічного вигляду: 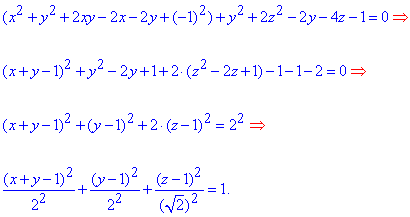
Тут всі маніпуляції з рівнянням поверхні повинні бути Вам зрозумілі.
Далі необхідно виконати заміну змінних
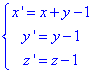
тоді отримаємо
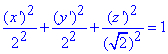
канонічне рівняння еліпсоїда обертання.
Наступним кроком необхідно визначити центр поверхні, для цього із перетвореного рівняння еліпсоїда виписуємо коефіцієнти:
a11=1, a22=2, a33=2, a12=1, a13=0, a23=0, a14=-1, a24=-2, a34=-2, a44=0.
З них складаємо СЛАР для знаходження центру еліпсоїда:
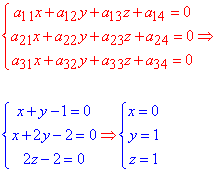
Точка O(0;1;1) - центр еліпсоїда.
Далі потрібно перенести початок координат в центр знайденого еліпсоїда, для цього виконуємо перетворення координат:
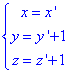
Звідси нові координати
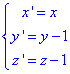
підставляємо в початкове рівняння
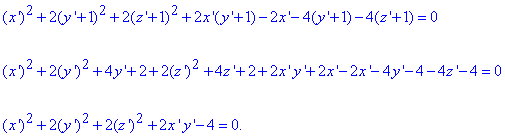
Останнє рівняння описує еліпсоїд в системі координат, що переміщена в центр еліпсоїда.
Багатьом з Вас готові відповіді на поверхні другого порядку стануть простою інструкцією з обчислень, іншим допоможуть зрозуміти теоретичний матеріал, в будь-якому разі матеріал піде Вам на користь.
Більше подібних матеріалів шукайте на сторінках сайту, тут добре описано поширені навчальні матеріалу для студентів математичних дисциплін.


