Центр поверхні другого порядку. Задачі

Продовжуємо цикл статтей з дослідження поверхонь другого порядку. Цього разу будемо аналізувати відповіді до завдань на знаходження центру поверхонь. Наведені приклади досить поширені, тому матеріал побудовано та, що після першого ознайомлення Ви самостійно змогли знайти правиьну відповідь.

Задачі на знаходження центру поверхні

Задача 6.3.1 б) Знайдіть центр поверхні другого порядку:
3x²-2y²+z²+2xy-2xz+8yz+4x+6y-12z-1=0
Розв'язання: Записуємо коефіцієнти рівняння поверхні другого порядку:
a₁₁=3, a₂₂=-2, a₃₃=1, a₁₂=1, a₁₃=-1,a₂₃=4, a₁₄=2, a₂₄=3,a₃₄=-6,a₄₄=-1.
Далі з їх допомогою складаємо систему трьох рівнянь для знаходження центру поверхні другого порядку.
Перетворюємо СЛАР методом Гауса:

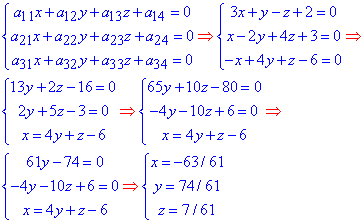
В результаті центром поверхні буде точка O(-63/61;74/61;7/61).

Задача в) Визначте координати центру поверхні другого порядку:
4x²+2y²+12z²-4xy+12xz+8yz+14x-10y+7=0.
Розв'язання: Знайдемо центр поверхні другого порядку (ПДП), взявши часткові похідні за правмлом

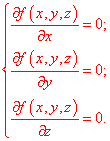
Для багатьох із Вас ця формула буде набагато корисніша і швидша, порівняно з виписуванням коефіцієнтів з рівняння поверхні та складання СЛАР.
Система рівнянь при обчисленні часткових похідних набуде вигляду

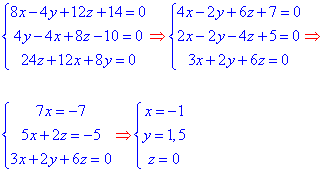
Після її зведення до східчастого вигляду розв'язуємо, в результаті можемо записати центр поверхні O(-1;1,5;0) у відповідь.

Задача г) Знайдіть геометричне мысце координат центру поверхні другого порядку:
5x²+9y²+9z²-12xy-6xz+12x-36z=0.

Розв'язання: Випишемо коефіцієнти рівняння заданої поверхні другого порядку:
a₁₁=5, a₂₂=9, a₃₃=9, a₁₂=-6, a₁₃=-3,a₂₃=0, a₁₄=6, a₂₄=0,a₃₄=-18,a₄₄=0.
Знайдемо центр поверхні другого порядку (ПДП) із СЛАР:

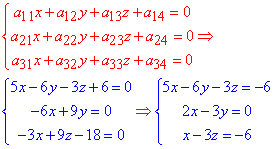
Систему рівнянь розв'яжемо методом Гауса, для цього складемо розширену матрицю системи лінійних рівнянь і зведемо до східчастого вигляду: третій рядок міняємо з першим місцями, далі утворюємо нулі під першим елементом - для цього від другого рядка віднімаємо подвоєний перше, а від третього віднімаємо перший помножений на (5). Далі 2 і 3 рядок нормуємо на (-3), після чого від 3 віднімаємо подвоєний 2.

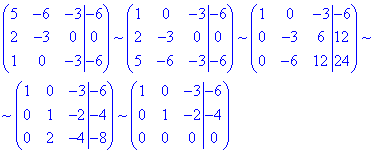
Оскільки ранг матриці r=2<3, то розв'язок системи рівнянь буде не точка, а пряма, яка є перетином площин, утвореної із останньої розширеної матриці:
x-3z+6=0;
y-2z+4=0.
Запишемо рівняння прямої в канонічному вигляді. Для цього знайдемо напрямний вектор площини і точку, що належить прямій. Напрямний вектор прямої в просторі p – це векторний добуток двох нормальних векторів площин n₁(1;0;-3) і n₂(0;1;-2), що утворюють пряму при перетині (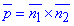). Векторний добуток знаходимо через визначник складений за формулою

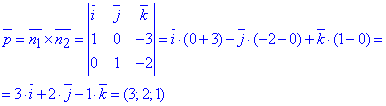
Знайдемо точку, що належить прямій (в просторі), нехай x=0, тоді підстановкою в рівняння площин знаходимо дві невідомі координати точки на прямій:

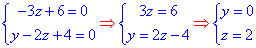
Таким чином маємо точку прямої M(0;0;2).
Маємо все дя того, щоб скласти канонічне рівняння прямої центрів заданої поверхні другого порядку: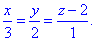

Уважно перегляньте, як було складене рівняння прямої, щоб наступного разу змогли повторити подібні обчислення.

Задача д) Знайдіть центр поверхні другого порядку:
5x²+2y²+2z²-2xy+2xz-4yz-4y-4z+4=0.
Розв'язання: З рівняння поверхні виписуємо коефіцієнти рівняння:
a₁₁=5, a₂₂=2, a₃₃=2, a₁₂=-1, a₁₃=1,a₂₃=-2, a₁₄=0, a₂₄=-2,a₃₄=-2,a₄₄=4.
Для знаходження центр поверхні другого порядку складаємо систему рівнянь: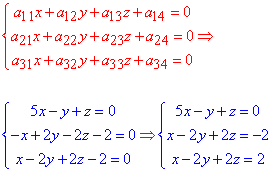

Її розв'яжемо методом Гауса, для цього випишемо розширену матрицю СЛАР і зведемо до східчастого вигляду: 5 і 1 рядок міняємо місцями і занулюємо елементи під першим.

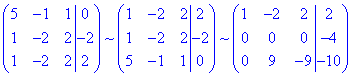
З другого рядка матриці робимо висновок, що система лінійних рівнянь несумісна, тому задана ПДП центра не має. Якщо б замість (-4) в правій частині мали нуль, то необхідно б було за методикою попереднтого прикладу знайти пряму перетину площин. Проте маємо несумісну СЛАР, що спрощує подальші обчислення і дозволяє зробити висновок що поверхня другого порядку не має центру.

Задача е) Визначте центр поверхні другого порядку:
x²-2y²+z²+6yz-4xz-8x+10y=0
Розв'язання: Випишемо коефіцієнти рівняння заданої поверхні другого порядку :
a₁₁=1, a₂₂=-2, a₃₃=1, a₁₂=0, a₁₃=-2,a₂₃=3, a₁₄=-4, a₂₄=5,a₃₄=0,a₄₄=0.
Знайдемо центр поверхні другого порядку (ПДП), розв'язавши СЛАР:

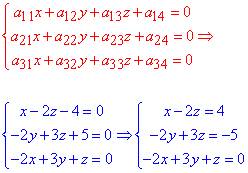
Систему рівнянь розв'яжемо методом Гауса, для цього складемо розширену матрицю системи лінійних рівнянь і зведемо її до східчастого вигляду:

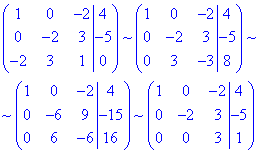
отримали трикутну систему рівнянь:

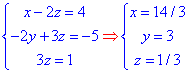
з якої знаходимо O(14/3; 3;1/3) - центр поверхні другого порядку.

Задача є) Знайдіть центр поверхні другого порядку:
4x²+y²+9z²-4xy+12xz-6yz+8x-4y+12z-5=0
Розв'язання: Центр поверхні знаходимо за алгоритмом, який добре розписаний в попередніх завданнях. Спершу запишемо коефіцієнти при рівнянні ПДП:
a₁₁=4, a₂₂=1, a₃₃=9, a₁₂=-2, a₁₃=6,a₂₃=-3, a₁₄=4, a₂₄=-2,a₃₄=6,a₄₄=-5.
Знайдемо центр поверхні другого порядку із СЛАР:

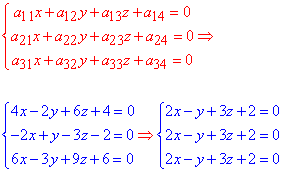
Із кінцевих співвідношень бачимо, що маємо три ідентичні рівняння тому робимо висновок, що задана поверхня другого порядку має площину центрів:
2x-y+3z+2=0.
Такі результати також можливі на практиці.

Задача ж) Знайдіть центр поверхні другого порядку:
x²+4y²+5z²+4xy-12x+6y-9=0
Розв'язання:Коефіцієнти рівняння поверхні другого порядку рівні:
a₁₁=1, a₂₂=4, a₃₃=5, a₁₂=2, a₁₃=0, a₂₃=0, a₁₄=-6, a₂₄=3, a₃₄=0, a₄₄=-9.
Центр поверхні другого порядку (ПДП) знаходимо із системи трьох рівнянь, яку складаємо з допомогою виписаних коефіцієнтів:

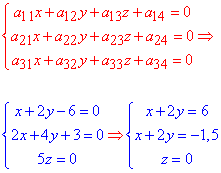
Отрима два рівняння, права частина яких відрізняється. Одночасно це неможливо, оскільки 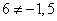, тому робимо висновок, що система рівнянь несумісна, і відповідно поверхня не має центра.

Задача з) Знайдіть центр поверхні другого порядку:
3x²+2y²+4yz-2xz-2x-8z-8=0
Розв'язання: Випишемо коефіцієнти рівняння заданої поверхні другого порядку:
a₁₁=3, a₂₂=2, a₃₃=0, a₁₂=0, a₁₃=-1, a₂₃=2, a₁₄=-1, a₂₄=0, a₃₄=-4, a₄₄=-8.
З коефіцієнтів складаємо рівняння на визначення центру поверхні другого порядку (ПДП):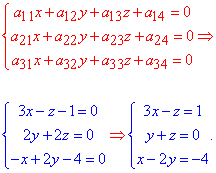

Систему рівнянь обчислюємо методом Гауса, для цього виписуємо розширену матрицю системи лінійних рівнянь і поступово спрощуємо її, щоб отримати східчастий вигляд:

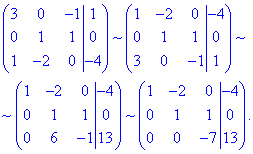
Далі в зворотньому порядку визначчаємо координати

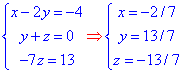
Звідси точка O(-2/7;13/7;-13/7) - центр ПДП.

Задача і) Знайдіть центр поверхні другого порядку:
x²+25y²+9z²-10xy+6xz-30yz-2x-2y=0
Розв'язання: З рівняння поверхні виписуємо коефіцієнти
a₁₁=1, a₂₂=25, a₃₃=9, a₁₂=-5, a₁₃=3, a₂₃=-15, a₁₄=-1, a₂₄=-1, a₃₄=0, a₄₄=0.
Складаємо систему трьох лінійних рівнянь, розв'язок якої і буде центром поверхні другого порядку (ПДП):

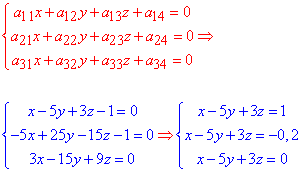
З аналізу 1 і 3 рівняння бачимо, що система рівнянь несумісна, оскільки 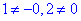, а це означає що поверхня не має центра.

Задача ж) Знайдіть центр поверхні другого порядку:
x²-14y²+10z²-4xy+6xz-24yz+2x+20y+8z-9=0.
Розв'язання: Щоб закріпити другий метод, який розглядали вище, знайдемо центр поверхні, взявши часткові похідні за формулою:

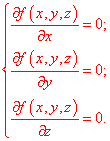
В результаті диференціювання отримаємо систему лінійних рівнянь, яку методом Гауса зводимо до східчастої

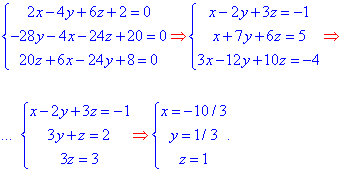
Звідси O(-10/3;1/3;1) - центр поверхні другого порядку.
Замість «…» зробили елементарні перетворення системи рівнянь, які можете повторити самостійно.
Наведені приклади служитимуть Вам доброю інструкцією з обчислення завдань на центр поверхні.
Збережіть матеріал в закладках та діліться посиланням на корисний матеріал з друзями.