Сьогодні розберемо чергову добірку показникових нерівностей, не найпростіших і не найскладніших. Приклади за 10-11 клас шкільної програми + теорія були дані в першій статті, тому їх перечитайте, якщо Вам важко розібрати, чому такі перетворення виконуємо та як переходимо від показникових нерівностей до дробовиих, квадратних та лінійних. Обчислення базуються на знанні властивостей показникових функцій, а їх коротко можна описати наступною схемою
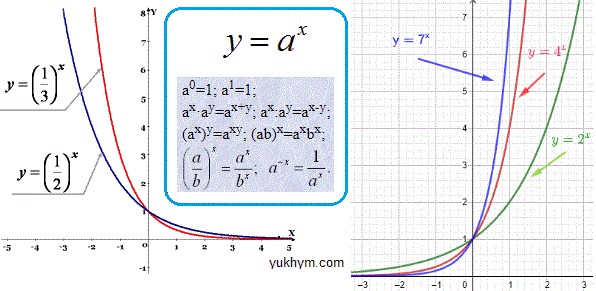
Тут Вам і основні формули додавання та множення степенів, графіки поведнки функцій при основах менше одиниці (зліва) та при основах більших за одиницю. Випадок коли основа рівна одиниці a=1 ви не знайдете, тому що це вертикальна пряма паралельна осі ординат, і при такому значенні немає що досліджувати та обчислювати.
Рівносильні перетворення показникових нервностей
Основа більша одиниці | Основа менша одиниці |
af(x)<ag(x)⇔f(x)<g(x); | af(x)<ag(x)⇔f(x)>g(x). |
Приклад 15.14 Розв'язати нерівність x2•3x-3x+1≤0.
Розв'язування: Розпишемо нерівність, винісши найменший показниковий вираз за дужки, та розклавши на прості множники вираз в дужках.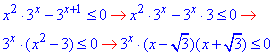
Показникова функція додатна 3x>0 для всіх x, тому на нерівнсть не впливає, тому її заміняємо еквівалентною нерівністю.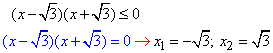
Далі методом інтервалів визначаємо знаки на інтервалах 
та виписуємо розв'язки нерівності x∈[-√3;√3].
Відповідь:[-√3;√3] – В.
Простих завдань, де маємо рівні основи та залишилося прирівняти степені тут не буде, вони розібрані на першому уроці. Тому, якщо щось не розумієте поверніться до основ, а можливо ще й додатково почитайте теорію.
Приклад 15.27 Розв’язати нерівність 2^(x2+3x)-8•2x>0.
У відповідь записати суму всіх цілих чисел, які не є розв’язками нерівності.
Розв'язування: Доданок зі знаком мінус перенесемо за знак нерівності, а далі обидві її частини розділимо на 2x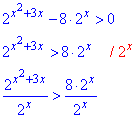
(Оскільки 2x>0 для всіх x, то ділення обох частин нерівності на цей вираз не змінює знаку)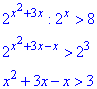
(знак нерівності при розкритті не змінили, тому що основа більша одиниці 2>1),
x2+2x>3
x2+2x-3>0,
x2+2x-3=0.
За теоремою Вієта отримаємо маємо:
x1=-3, x2=1.
Будуємо числову всь та точки, визначаємо знаки 
звідси x∈(-∞;-3)∪(1;+∞).
Випишемо усі цілі числа, які не є розв’язками нерівності і знайдемо їх суму:
-3; -2; -1; 0; 1.
-3+(-2)+(-1)+1=-5.
Відповідь:-5.
ЗНО 2018. Завдання 18. Розв'яжіть нерівність 2^x+2^2x+3≥144.
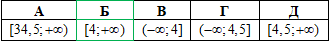Розв'язування: Винесемо найменший степінь в лівій частині нерівності та згрупуємо решту доданків.
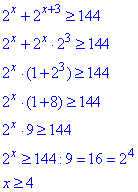
"Ікс" належить інтервалу x∈[4;+∞).
Відповідь: x∈[4;+∞) – Б.
Приклад 15.28 Розв’язати нерівність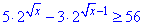 
У відповідь записати найменший цілий розв’язок нерівності.
Розв'язування: Випишемо для коренів у показнику ОДЗ: x≥0
Далі 2√x виносимо з перших двох доданків, а все що при цьому залишилося переносимо в праву сторону та зводимо до степенів 2.
Далі при рівних основах 2>1 порівнюємо степені: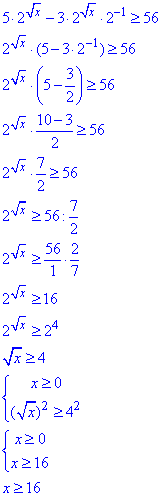 
Наносимо корені на числову вісь 
та записуємо у вигляді інтервалу x∈[16;+∞).
Звідси, x=16 – найменший цілий розв’язок.
Відповідь:16.
Приклад 15.29 Розв’язати нерівність 2x+2-x+1-3<0.
У відповідь записати координату середини проміжку, який є розв’язком нерівності.
Розв'язування: Помножимо обидві частини нерівності на 2x, щоб спростити. Оскільки множимо на додатний вираз 2x>0, то знак нерівності при цьому не міняємо,.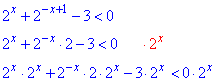
Далі перепишемо нерівність під вигляд квадратної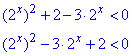
Заміна:
2x=t, де t>0,
t2-3t+2<0
Корені рівняння
t2-3t+2=0
знаходимо за теоремою Вієта:
t1+t2=3,
t1•t2=2.
Звідси t1=1, t2=2.
Нерівність строга, тому знайдені точки виколюємо на числовій осі, та підстановкою нуля t=0 визначаємо знаки на інтервалах +,-,+.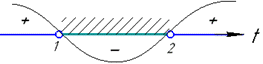
Звідси t∈(1;2).
Повертаємося до заміни та обчислюємо прості показникові нерівності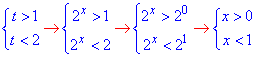
x∈(0;1) – шуканий розв’язок.
Краї інтервалу маємо, можемо знайти координату середини проміжку:
(0+1)/2=0,5.
Відповідь:0,5.
Приклад 15.33 Розв’язати нерівність 2•4x-5•6x+3•9x<0.
У відповідь записати координату середини проміжку, який є розв’язком нерівності.
Розв'язування: Перетворимо показникові вирази до основ рівних 2 та 3, після чого розділимо на 3x, знаку це не поміняє.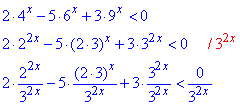
В результаті отримаємо квадратичну нерівність відносно (2/3)x
тому виконуємо заміну: (2/3)x=t, де t>0,
та для розкриття нерівності 2t2-5t+3<0 обчислюємо квадратне рівняння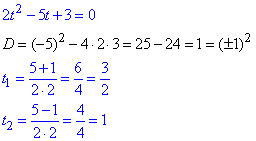
Методом інтервалів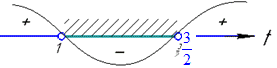 
визначаємо t∈(1;3/2).
Не забуваємо про заміну та розписуємо прості показникові нерівності, також пам'ятайте, що основа 2/3<1, тому при розкритті знак нерівності міняємо на протилежний.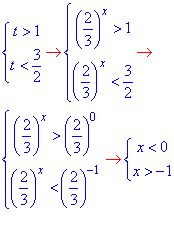
x∈(-1;0) – розв’язок.
Знайдемо координату середини проміжку:
(-1+0)/2=-0,5.
Відповідь:-0,5.
З готових відповідей до ЗНО прикладів Ви мали б навчитися не тільки, як обчислювати показникові нерівності, а й правильного оформлення відповідей. На практичних, олімпіадах та ЗНО тестах звертають увагу не тільки на кінцеву правильну чи ні відповідь, а й на хід думок, порядок оформлення обчислень. Тому і Ви на це звертайте увагу, та вчіться стисло та зрозуміло доносити викладачам, що й для чого Ви робили при розв'язуванні.
