Продовжуємо розв'язувати ірраціональні рівняння і ділитися схемами розкриття квадратних та кубічних коренів. Завдання взяті із програми підготовки школярів до ЗНО тестів, тому в певній мірі охоплюють всі теми, що Вас вчили у школі. Якщо Ви навчитеся розв'язувати наведені приклади, то всі решта будуть однотипними. Аналізуйте відповіді та запам'ятовуйте кращі методики та схеми отримання розв'язків.
Приклад 12.5 Знайти суму коренів рівнянь
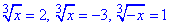
А | Б | В | Г | Д |
-20 | -18 | 0 | 12 | 9 |
Обчислення: Маємо три найпростіших кубічних рівняння. Щоб їх розв'язати обидві сторони рівняння піднести до кубу.
Виконаємо розрахунки
1. 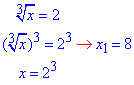
2.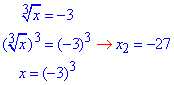
3. 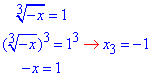
x1=8; x2=-27; x3=-1 - корені заданих рівнянь.
За умовою, знайдемо їх суму:
x1+x2+x3=8-27-1=20.
Відповідь: -20 – А.
Приклад 12.6 Знайти суму коренів рівнянь
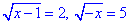
А | Б | В | Г | Д |
30 | -20 | 8 | -7 | -24 |
Обчислення:Задані прості ірраціональні рівняння з одним коренем квадратним в лівій частині та числом в правій.
Для їх обчислень необхідно обидві частини від знаку рівності піднести до квадрату. Попередньо встановимо області визначення.
1. 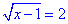
ОДЗ: x-1≥0, звідси x≥1.
Остаточно x∈[1;+∞).
Для розкриття ірраціональності підносимо рівняння до квдрату
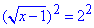
x-1=4, x=4+1=5, звідси x1=5.
2. 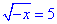
ОДЗ: -x≥0, звідси x≤0.
Отже, x∈(-∞;0].
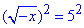
-x=25 , звідси x2=-25.
Обидва корені заданих рівнянь належать ОДЗ, тому знайдемо їх суму:
x1+x2=5-25=-20.
Відповідь: -20 – Б.
Приклад 12.7 Яке з наведених рівнянь має корені?
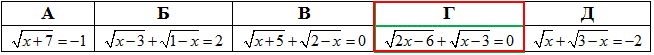 Обчислення: Проведемо швидкий аналіз рівнянь. Варіанти А
Обчислення: Проведемо швидкий аналіз рівнянь. Варіанти А 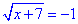 та Д
та Д 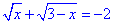 не мають коренів,
не мають коренів,
оскільки значення кореневих функції 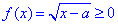 повинні бути додатні.
повинні бути додатні.
В нас же в правій стороні -1<0 і -2<0 відповідно.
Перевіримо інші пункти.
Б. 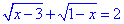
Обмеження на ОДЗ:
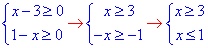
Область визначення порожня множина x∈∅, тому рівняння не має коренів.
В. Рівняння 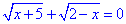 має корені, якщо кожен з коренів при однаковій змінній рівний нулю
має корені, якщо кожен з коренів при однаковій змінній рівний нулю
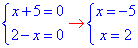
Розв'язуючи кожне з рівнянь системи, маємо 2+5≠0, тому саме рівняння 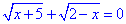 не має коренів.
не має коренів.
Г. Рівняння 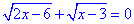 має корені, якщо корені квадратні одночасно рівні нулю
має корені, якщо корені квадратні одночасно рівні нулю
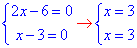
Звідси слідує, що рівняння 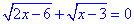 має єдиний корінь, а саме x=3.
має єдиний корінь, а саме x=3.
Відповідь: 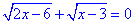 – Г.
– Г.
Приклад 12.8 Знайти значення виразу 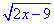 , якщо значення x задовольняє умову
, якщо значення x задовольняє умову 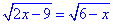
А | Б | В | Г | Д |
∅ | 5 або -1 | 1 або -1 | 5 | 1 |
Обчислення: Розв'яжемо ірраціональне рівняння:
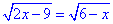
Підкореневі функції повинні приймати невід'ємні значення, звідси маємо систему нерівностей для області визначення:
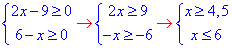
остаточно x∈[4,5;6].
Щоб позбутися радикала підносимо обидві частини до квадрату
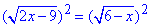
2x-9=6-x,
2x+x=6+9,
3x=15, звідси x=5.
Оскільки x=5 належить ОДЗ, то він є розв'язком.
Підставимо знайдений корінь в початкову умову
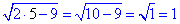
Відповідь: 1 – Д.
Приклад 12.9 Знайти значення виразу √(x+11), якщо значення x задовольняє умову 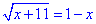
А | Б | В | Г | Д |
3 або 4 | 3 або -3 | 3 | 4 або -4 | 4 |
Обчислення: Розв'язок рівняння розпочнемо з аналізу ОДЗ:
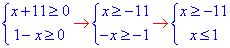
тобто x∈[-11;1].
Для розкриття ірраціональності піднесемо обидві частини рівняння до квадрату
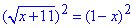
x+11=1-2x+x2,
x2-3x-10=0,
звідси x1=-2 і x2=5.
Корінь x2=5 не належить області визначення, тому лише x=-2 є розв'язком рівняння.
Отже, 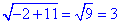
Відповідь: 3 – В.
Приклад 12.10 Знайти суму коренів рівняння 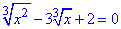
А | Б | В | Г | Д |
9 | -9 | 3 | -3 | 2 |
Обчислення: Такого змісту ірраціональні рівняння обчислюють методом заміни змінної.
Позначимо через параметр другий доданок:
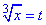 , тоді
, тоді 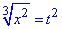
При підстановці отримаємо квадратне рівняння
t2-3t+2=0, звідси t1=1 і t2=2.
Повертаємося до заміни змінних та виконуємо обчислення кубічних рівнянь
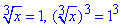
звідси x1=1.
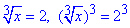
звідси x2=8.
Знайдемо суму розв'язків рівняння:
x1+x2=1+8=9.
Відповідь: 9 – А.
Приклад 12.11 Розв'язати рівняння 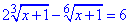
А | Б | В | Г | Д |
∅ | -4-3/8; 7 | 7 | -7 | 63 |
Обчислення: Другий корінь має парний степінь (6), тому випишемо спершу ОДЗ:
x+1≥0, звідси x≥-1, тобто x∈[-1;+∞).
Перетворимо ірраціональне рівняння до вигляду
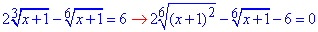
Звідси бачимо, яку заміну змінних слід застосувати:
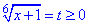 , тоді
, тоді 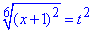
Розв'яжемо квадратне рівняння, яке при цьому отримаємо
2t2-t-6=0,
D=(-1)2-4•2•(-6)=1+48=49=(±7)2,
звідси
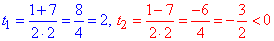
Другий корінь не задовольняє область визначення.
Повертаємося до заміни змінних та знаходимо розв'язок
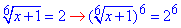
x+1=64,
x=64-1=63.
Відповідь: 63 – Д.
Приклад 12.12 Скільки коренів має рівняння 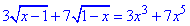 ?
?
А | Б | В | Г | Д |
Жодного | один | два | три | >3 |
Обчислення: На вигляд маємо складне ірраціональне рівняння, але погляньте далі як спроститься пошук коренів внаслідок дослідження області визначення:
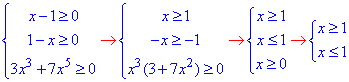
звідси x=1.
Таким чином, розв'язком ОДЗ є лише одне число, а саме 1, тому підставимо його у початкове рівняння і перевіримо, чи є це число його коренем:
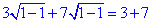 , 0=8, отже, задане рівняння коренів не має.
, 0=8, отже, задане рівняння коренів не має.
Відповідь: Жодного – А.
Приклад 12.13 Скільки цілих коренів має рівняння
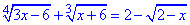 ?
?
А | Б | В | Г | Д |
Жодного | один | два | три | чотири |
Обчислення: Маємо ірраціональне рівняння в яке входять корені різних порядків.
Спершу звузимо множину розв'язків через визначення ОДЗ:
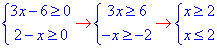
звідси отримали значення x=2.
Розв'язком ОДЗ є лише одне число, а саме 2, тому підставимо його у задане рівняння і перевіримо, чи є це число його коренем:
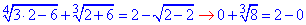 , тобто 2=2,
, тобто 2=2,
отже, задане рівняння має один цілий корінь, а саме x=2.
Відповідь: один – Б.
Розкриття ірраціональностей та обчислення коренів рівнянь не є важким завданням, якщо знати властивості кореневих функцій, бачити в яких випадках та і яку робити заміну. А для цього потрібна довга і важка самостійна робота, і чим більше прикладів Ви виконаєте, тим легше буде на практиці.
Попереду ще понад 30 завдань, як краще розкривають тему та допомагають підготуватись до ЗНО тестувань.


