Посібник для підготовки до зовнішнього незалежного тестування з математики
Відповіді до посібника для підготовки до ЗНО тестування допоможуть Вам швидко пройти шкільний матеріал, пригадати усі теми, що можуть чекати Вас та скласти тести з успішним результатом.
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Завантажити (скачати) відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики). Формат: PDF
Зміст: Посібник містить поради щодо проходження ЗНО з математики та взірці тестових завдань.
Усі задачі однієї теми розміщені в порядку складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.
Рік випуску: 2010 р.
Тема 1. Арифметичні приклади та задачі
Розберемо приклади на знання форм записів чисел, вміння підносити до степення та спрощувати дроби.
Приклад 1.23 Установити відповідність між числами (1–4) та їх остачами від ділення на 9 (А – Д).
1. 53229465
2. 81720245
3 3. 333333332
4 4. 33333016
А. 2
Б. 3
В. 4
Г. 5
Д. 0
Обчислення: За ознаками подільності – число націло ділиться на 9, якщо сума його цифр ділиться на 9.
За цим же правилом визначаємо остачу від ділення
1. 5+3+2+2+9+4+6+5=36, звідси остача 0.
1 – Д.
2. 8+1+7+2+0+2+4+5=29, звідси остача 2.
2 – А.
3. 3+3+3+3+3+3+3+2=23, звідси остача 5.
3 – Г.
4. 3+3+3+3+3+0+1+6=22, звідси остача 4.
4 – В.
Приклад 1.24 Установити відповідність між числами (1–4) та їх записами у стандартному вигляді (А – Д).
Обчислення: Перетворюємо записи чисел до цілих, помножених на 10 у відповідному показнику.
Приклад 1.25 Установити відповідність між періодичними десятковими дробами (1–4) та їх записами у вигляді звичайних дробів (А – Д).
Обчислення: Умова дещо складніша від попереднього прикладу, проте і такі завдання Ви повинні вміти зробити з курсу шкільної математики.
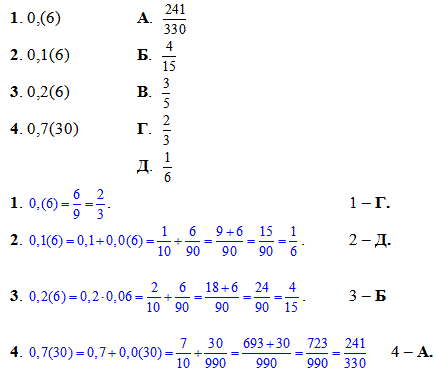
Приклад 1.26 Установити відповідність між виразами (1–4) та їх значеннями (А – Д).
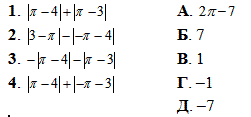
Обчислення: Завдання на знання модулів.
Тут потрібно врахувати, що число Pi менше за 4 та більше за 3.
На основі цього розкриваємо модулі
1. 
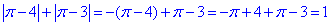1 – В.
2. 
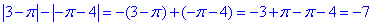2 – Д.
3. 
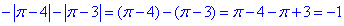3 – Г.
4. 
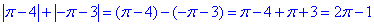2 – А.
Приклад 1.27 Установити відповідність між виразами (1–4) та їх значеннями (А – Д).
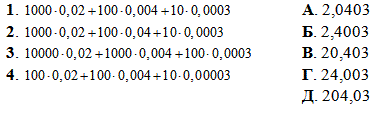
Обчислення: Спрощуємо вирази та знаходимо якій з відповідей тесту належить кінцеве значення.
1. 1000•0,02+100•0,004+10•0,0003=20+0,4+0,003=20,403 – В.
2. 1000•0,02+100•0,04+10•0,0003=20+4+0,003=24,003 – Г.
3. 10000•0,02+1000•0,004+100•0,0003=200+4+0,03=204,03 – Д.
4. 100•0,02+100•0,004+10•0,00003=2+0,4+0,0003=2,4003. – Б.
Приклад 1.28 Установити відповідність між виразами (1–4) та їх значеннями (А – Д).
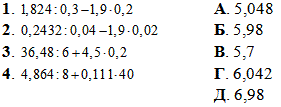
Обчислення: Перетворюємо вирази, а далі в зручний спосіб виконуємо ділення та множення, після чого сумування
1. 1,824:0.3-1,9•0,2=18,24:3-0,38=6,08-0,38=5,7.
1 – В.
2. 0,2432:0,04-1,9•0,02=6,08-0,038=6,042.
2 – Г.
3. 36,48:6+4,5•0,2=6,08+0,9=6,98.
3 – Д.
4. 4,864:8+0,111•40=0,608+4,44=5,048.
4 – А.
Приклад 1.29 Установити відповідність між виразами (1–4) та їх значеннями (А – Д).
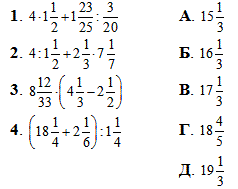
Обчислення: Приклади потрібно обчислювати уважно, оскільки найменша помилка при зведенні чисел з остачею до дробів може обернутися неправильною відповіддю.
Загалом у завданнях з дробами не варто поспішати!
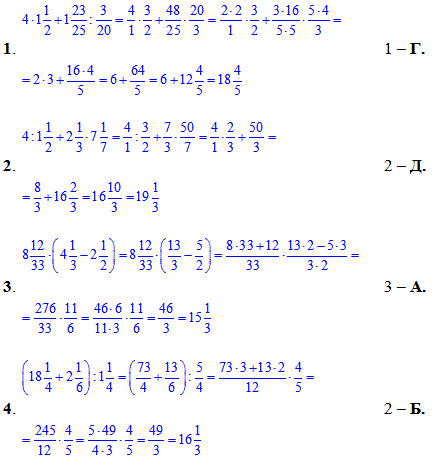
Приклад 1.30 Установити відповідність між виразами (1–4) та їх значеннями (А – Д).
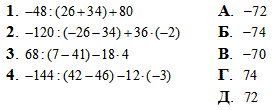
Обчислення: Знаходимо значення виразів та порівнюємо з варіантами відповідей
1. -48(-26+34)+80=-48:8+80=-6+80
1 – Г.
2. -120(-26-34)+36•(-2)=-120(-60)-72=2-72=-70.
2 – В.
3. 68:(7-41)-18•4=68:(-34)-72=-2-72=-74.
3 – Б.
4. -144:(-4)-12•(-3)=36+36=72.
4 – Д.
Приклад 1.31 Установити відповідність між степенями (1–4) та їх значеннями (А – Д).
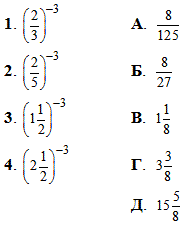
Обчислення: Зводимо дроби з остачею до спільного знаменника, а далі виконуємо піднесення до кубу
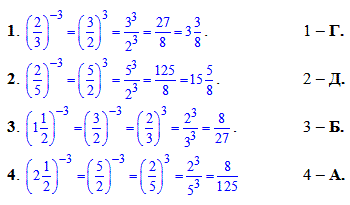
Приклад 1.32
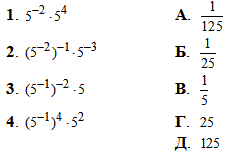
Обчислення: За правилом піднесення до степеня, задані вирази мають спільну основу.
Тому спершу знаходимо показники (сумуємо, множимо), а далі підносимо до знайденого степеня
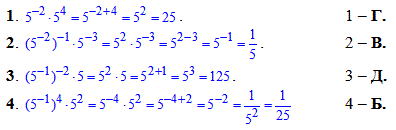
Приклад 1.34 Обчислити зручним способом: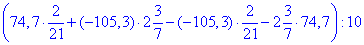 
Обчислення: Мамо завдання на спрощення виразу, що містить дроби.
Спершу розписуємо та спрощуємо вираз в дужках, а далі виконуємо ділення на 10.
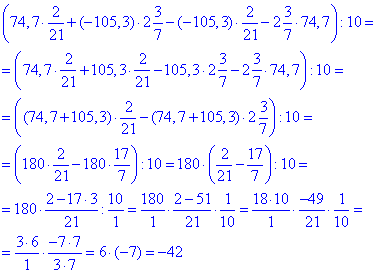
Відповідь: –42.
Приклад 1.35 Знайти невідомий член пропорції:
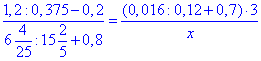
Обчислення: Обчислимо чисельники та знаменник пропорції окремо.
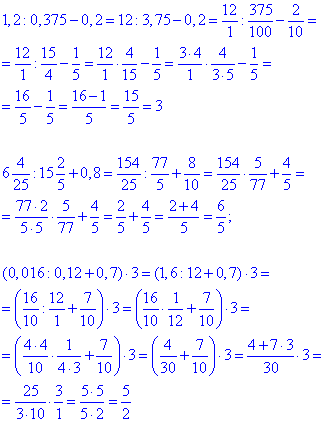
Далі підставляємо в пропорцію та записуємо в зручній для читання формі
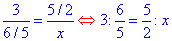
Розв'яжемо пропорцію (добуток крайніх членів = добутку середніх):
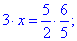
3•x=6/2;
x=1.
Відповідь: 1.
Приклад 1.43 Знайти x, якщо
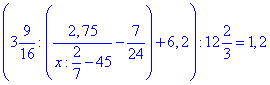
Обчислення: Спростимо всі вирази, які можливо, а далі розв'язуємо рівняння відносно невідомої.
Так як маємо справу з дробами, то всі дії слід виконувати уважно та без спішки.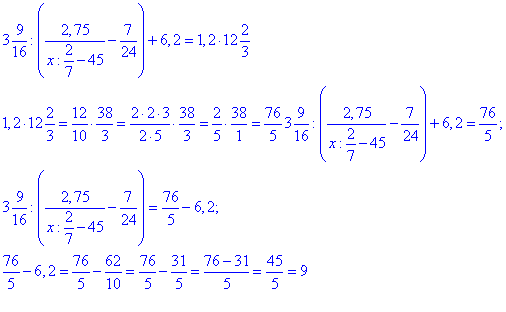
В результаті обчислень отримаємо натуральне число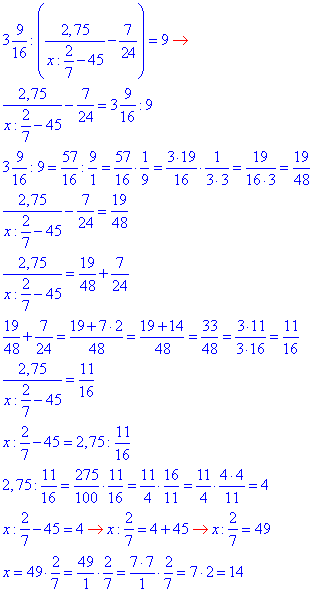 
x=14.
Відповідь: 14.
