Посібник для підготовки до зовнішнього незалежного тестування з математики
Підручник для 11 класу:
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Завантажити (скачати) відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики). Формат: PDF
Зміст: Посібник містить поради щодо проходження ЗНО з математики та взірці тестових завдань. Усі задачі однієї теми розміщені в порядку складності. Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.
Рік випуску: 2010 р.
Тема: Відсотки
На попередньому уроці ми розібрали відповіді до простих задач на відсотки, тут спробуємо викласти своє бачення, як потрібно обчислювати тестові завдання при проходженні ЗНО тестування.
Завдання 2.20 Тривалість робочого дня зменшилась з 8 год до 6 год. На скільки відсотків потрібно підвищити продуктивність праці, щоб випуск продукції залишився тим же?
Обчислення: Нехай x - кількість продукції, що випускають за один день,
x/8 - продуктивність повного робочого дня (приймаємо за 100%);
x/6 - продуктивність неповного робочого дня., тоді,
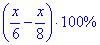- відсоткова різниця в продуктивності:
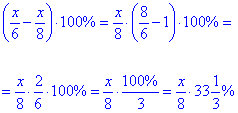
Оскільки випуск продукції повинен залишитися як для повного робочого дня, то на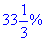 
потрібно підвищити продуктивність праці.
Відповідь: 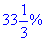– В.
Завдання 2.21 Машиніст провів поїзд за 7 год 30 хв замість 9 год за графіком. На скільки відсотків було збільшено середню швидкість.
Обчислення: 7 год 30 хв = 7,5 год.
Оскільки середня швидкість змінювалась пропорційно до затраченого часу, то знайдемо скільки відсотків становить число 9 від 7,5.
Запишемо коротку умову:
7,5 – 100%
9 – x.
Звідси складемо пропорцію:
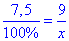
або 7,5:100%=9:x.
Розв'яжемо пропорцію (добуток крайніх членів = добутку середніх):
7,5•x=9•100% звідки
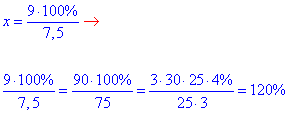
тому 120%-100%=20%.
На 20% було збільшено середню швидкість поїзда.
Відповідь: 20% – А.
Завдання 2.22 У сплаві міді та цинку мідь становить 1/7 частину маси цинку. Який відсотковий уміст міді у сплаві?
Обчислення: Нехай x - маса міді у сплаві,
y - маса цинку у сплаві, тоді x=y/7 (за умовою задачі),
а x+y - маса сплаву (приймаємо за 100%).
Якщо x=y/7, то y=7x, тоді
x+y=7x+x,
x+y=8x, звідси
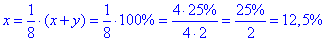- вміст міді у сплаві.
Відповідь: 12,5% – Б.
Завдання 2.23 2 кг сплаву міді з оловом містить 40% міді. Скільки потрібно додати до цього сплаву олова, щоб отриманий сплав містив 16% міді.
Обчислення: 1) Знайдемо масу міді в початковому сплаві.
Запишемо коротку умову:
2 кг – 100%
х кг – 40 % .
Звідси складемо пропорцію:
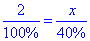
або 2:100%=x:40%.
Розв'яжемо пропорцію (добуток крайніх членів = добутку середніх):
2•40%=x•100% звідки
, 
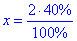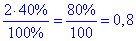
отже 0,8 кг – маса міді у сплаві.
Тоді 2-0,8=1,2 кг – маса олова у сплаві.
2) Знайдемо масу утвореного сплаву з додаванням олова у попередній сплав: Запишемо коротку умову:
y кг – 100%
0,8 кг – 16 % .
Звідси складемо пропорцію:
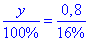
або y:100%=0,8:16%.
Розв'яжемо пропорцію (добуток крайніх членів = добутку середніх):
y•16%=0,8•100% звідки
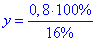
отже 5 кг – маса утвореного сплаву.
Тоді 5-2=3 кг – маса олова у сплаві, якого потрібно додати, щоб отриманий сплав містив 16% міді.
Відповідь: 3кг – А.
Завдання 2.24 Установити відповідність між частинами (1–4) та відсотками (А–Д).
1. 1/4
2. 2/5
3. 1/8
4. 4/5
А. 40%
Б. 20%
В. 80%
Г. 12,5%
Д. 25%
Обчислення:
1) 1/4•100%=25% - Д;
2) 2/5•100%=40% - А;
3) 1/8•100%=1/2•1/4•100%4=1/2•25%=12,5% - Г;
4) 4/5•100%=4•20%=80% - В.
Завдання 2.25 Установити відповідність між затушованими частинами круга (1–4) та відсотками (А–Д), які вони становлять від круга.
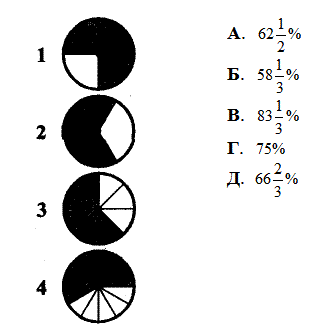
Обчислення:
Завдання 2.26 Установити відповідність між задачами (1–4) та їх розв'язаннями (А–Д).
1. Скільки відсотків становить число 40 від числа 240?
2. Знайти 40% від числа 240.
3. Знайти число, 40% якого дорівнюють 240.
4. Скільки відсотків становить число 240 від числа 40? А.
Обчислення: Коротка умова – пропорція – розв'язок:
1) 240 – 100%
40 – x % , звідси
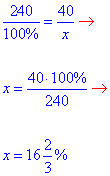- Д;
2) 240 – 100%
x – 40% , звідси
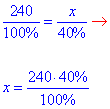
x=96 - А;
3) x – 100%
240 – 40 % , звідси
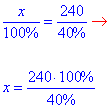
x=600 - Г;
4) 40 – 100%
240 – x % , звідси
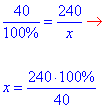
x=600% - В.
Завдання 2.27 Кількість дівчат у класі становить 1/4 кількості хлопців. Установити відповідність між задачами (1–4) та відповідями (А–Д) до них.
1. Скільки відсотків хлопців у класі?
2. Скільки відсотків дівчат у класі?
3. Знайти відсоткове відношення кількості дівчат до кількості хлопців.
4. Знайти відсоткове відношення кількості хлопців до кількості дівчат.
А. 20%
Б. 75%
В. 25%
Г. 80%
Д. 400%
Обчислення: Нехай x - кількість дівчат у класі, y - кількість хлопців у класі, тоді x=y/4 (за умовою задачі),
а x+y - загальна кількість дітей в класі (їх 100%).
1) Якщо x=y/4, то
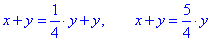
звідси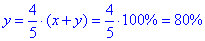 
отож 80% хлопців - Г;
2) 100%-80%=20% дівчат - А;
3) Якщо x=y/4, то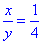 
, тобто 100%:4=25% - В;
4) Якщо x=y/4, то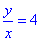 
, тобто 4•100%=400% - Д.
Завдання 2.28 Установити відповідність між задачами (1–4) та відповідями (А–Д) до них.
1. Вкладник вніс до банку 11000 грн під 13% річних. Скільки гривень становитиме прибуток через рік?
2. Вкладник вніс до банку 11000 грн під 12% річних. Скільки гривень буде на його рахунку через рік?
3. Вкладник вніс до банку 4000 грн під 16% річних. Скільки гривень становитиме прибуток через 2 роки?
4. Вкладник вніс до банку 1000 грн під 20% річних. Скільки гривень буде на його рахунку через 2 роки?
А. 12320
Б. 1382,4
В. 1340
Г. 1430
Д. 1440
Обчислення: Запишемо формулу складних відсотків:
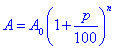
де A0 - початковий вклад;
A - кінцева сума;
p, % - річна ставка;
A-A0 - прибуток;
n - кількість років.
1) A0=11000 грн, p=13%, n=1 рік, A-A0 - ?
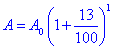
A=A0+0,13A0, звідси A-A0=0,13A0,
A-A0=0,13•11000=1430 грн - Г;
2) A0=11000 грн, p=12%, n=1 рік, A - ?
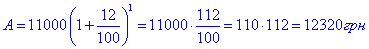- А;
3) A0=4000 грн, p=16%, n=2 роки, A-A0 - ?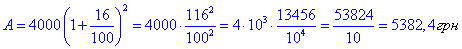 
A-A0=5382,4-4000=1382,4 грн - Б;
4) A0=1000 грн, p=20%, n=2 рік, A - ?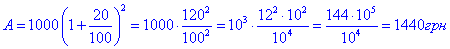 
- Д.
Завдання 2.30 Скільки кілограмів води потрібно випарувати зі 100 кг 10%-го розчину солі, щоб одержати розчин з концентрацією 20%?
Обчислення: 1) Знайдемо масу солі в початковому розчині.
Запишемо коротку умову:
100 кг – 100%
x кг – 10%.
Звідси складемо пропорцію:
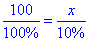
або 100:100%=x:10%.
Розв'яжемо пропорцію (добуток крайніх членів = добутку середніх):
100•10%=x•100% звідки
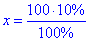
отже x=10 кг – маса солі у початковому розчині.
Тоді 100-10=90 кг – маса води в початковому розчині.
2) Знайдемо масу утвореного розчину (після випаровування води):
Запишемо коротку умову:
y кг – 100%
10 кг – 20%.
Звідси складемо пропорцію:
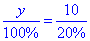
або y:100%=10:20%.
Розв'яжемо пропорцію (добуток крайніх членів = добутку середніх):
y•20%=10•100% звідки
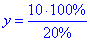
отже y=50 кг – маса утвореного розчину.
Тоді 100-50=50 кг – маса води, яку потрібно випарувати, щоб одержати розчин з концентрацією 20%.
Відповідь: 50 кг.
Завдання 2.32 З молока одержують 21% вершків, а з вершків – 24% масла. Зі скількох тон молока можна одержати 126 кг масла?
Обчислення: 1) Знайдемо масу вершків, з яких одержують 126 кг масла. Запишемо коротку умову:
x кг - 100%
126 кг - 24 %.
Звідси складемо пропорцію:
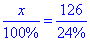або x:100%=126:24%.
Розв'яжемо пропорцію (добуток крайніх членів = добутку середніх):
x•24%=126•100% звідки
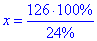
отже x=525 кг вершків треба для 126 кг масла.
2) Знайдемо масу молока, з яких одержують 525 кг вершків. Запишемо коротку умову:
y кг - 100%
525 кг - 21 %.
Звідси складемо пропорцію:
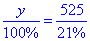
або y•21%=525•100%.
Розв'яжемо пропорцію (добуток крайніх членів = добутку середніх):
y•21%=525•100% звідки
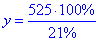
отже y=2500 кг молока треба для 525 кг вершків.
2500 кг = 2,5 т.
Отже, з 2,5 т молока можна одержати 126 кг масла.
Відповідь: 2,5 т.
