Посібник для підготовки до зовнішнього незалежного тестування з математики
Підручник для 11 класу:
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Завантажити (скачати) відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики). Формат: PDF
Зміст: Посібник містить поради щодо проходження ЗНО з математики та взірці тестових завдань. Усі задачі однієї теми розміщені в порядку складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.
Рік випуску: 2010 р.
Тема: Відсотки
Основні рекомендації, як розв'язувати задачі на відсотки Ви можете почитати в посібнику для підготовки до ЗНО.
Тут будуть наведені готові відповіді до задач, які оформлені відповідно до рекомендацій збірника завдань.
Завдання 2.1 Як знайти 52% від числа 960?
Обчислення: Запишемо коротку умову:
960 – 100%
x- 52% .
Звідси складемо пропорцію:
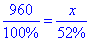
або
960:100%=x:52%.
Розв'яжемо пропорцію за правилом (добуток крайніх членів = добутку середніх):
960•52%=x•100% звідки
,
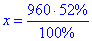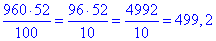
тобто шуканий відсоток рівний x=499,2.
Відповідь: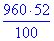 
– В.
Завдання 2.2 Як знайти число, 60% якого дорівнюють 360?
Обчислення: Запишемо умову до прикладу:
x – 100%
360 – 60% .
Далі складаємо пропорцію:
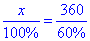
або x:100%=360:60%.
Обчислимо пропорцію (добуток крайніх членів = добутку середніх):
x•60%=360•100% звідки
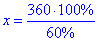
тобто x=600.
Відповідь: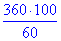 
– Д.
Завдання 2.3 Як встановити, скільки відсотків становить число 9 від 96?
Обчислення: Запишемо коротку умову:
96 – 100%
9 – x% .
Складемо пропорційне рівняння:
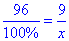
або 96:100%=9:x%.
Розв'яжемо пропорцію (добуток крайніх членів = добутку середніх):
96•x=9•100% звідки
,
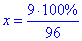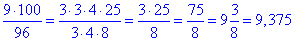
тобто x=9,375%.
Відповідь: А.
Завдання 2.4 Банк сплачує своїм вкладникам 8% річних. Визначити, скільки грошей потрібно внести на рахунок, щоб через рік отримати 60 грн. прибутку.
Обчислення: Запишемо формулу складних відсотків: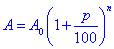 
, де
A0 - початкова величина, (початковий вклад);
A - кінцева величина,
A-A0=60 грн. – прибуток; p,% ,
p=8% - відсоткове змінення величини;
n=1 - час змінення величини.
Оскільки A-A0=60, то звідси маємо A =60+A0.
Таким чином отримаємо
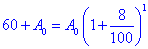
розв'яжемо рівняння відносно A0:
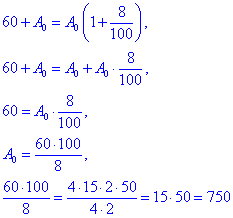
отже A0=750 грн.
Відповідь: 750 грн – Д.
Завдання 2.5 Уміст олова у сплаві становить 40%. Скільки грамів олова у 300 г такого ж сплаву?
Обчислення: Запишемо коротку умову:
300г – 100%
x – 40% .
Звідси складемо пропорцію:
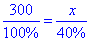
або 300:100%=x:40%.
Визначимо невідому з пропорції (добуток крайніх членів = добутку середніх):
300•40%=x•100% звідки
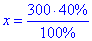
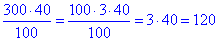
отже x=120 г.
Відповідь: 120 г – Б.
Завдання 2.6 Сплав містить 50 г олова і 200 г міді. Який відсотковий уміст олова у сплаві?
Обчислення: Завдання на сплави важкі для багатьох школярів, тому уважно розьеріть схему обчислень
1) 50+200=250 г – маса сплаву.
2) Складаємо умову:
250 – 100%
50 – x%. .
Звідси будуємо пропорцію:
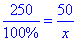
або 250:100%=50:x.
Розв'яжемо пропорцію:
250•x=50•100% звідки
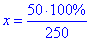
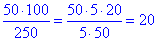
отже x=20%.
Відповідь: 20% – В.
Завдання 2.7 Вкладник вніс до банку 2000 грн., а через рік отримав 2160 грн. Під який відсоток річних були покладені гроші?
Обчислення: Запишемо формулу складних відсотків:
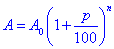
де A0=200 грн,
A=2160 грн,
n=1,
p,%?
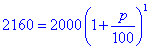
розв'яжемо рівняння відносно p:
2160=2000+20p,
20p=160,
p=160:20=8%.
Відповідь: 8% – Б.
Завдання 2.8 10%-й розчин солі містить 180 г води. Яка маса цього розчину?
Обчислення: 1) Знаходимо 100%-10%=90% – вміст води у розчині.
2) Запишемо умову до прикладу:
x – 100%
180 – 90% .
Звідси складемо пропорцію:
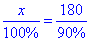
або x:100%=180:90% .
Розв'яжемо пропорцію :
x•90%=180•100% звідки
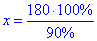
отже x=200 г.
Відповідь: 200 г – Г.
Завдання 2.9 Ціна товару дорівнює 64 грн.
Після зниження ціни товар коштував 56 грн.
На скільки відсотків було знижено ціну?
Обчислення: Обчислимо, скільки відсотків становить нова ціна товару від початкової
1) Запишемо коротко умову завдання:
64 – 100%
56 – x% .
Звідси складемо пропорцію:
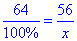
або 64:100%=56:x.
Розв'яжемо пропорцію:
64•x=56•100% звідки
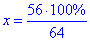
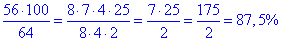
отже x=87,5%.
Обчислимо, на скільки відсотків знизилась ціна товару:
2) 100%-87,5%=12,5% - зниження товару.
Відповідь: 12,5% – Д.
Завдання 2.10 Скільки відсотків від 180 становлять 15% від 300?
Обчислення: 1) Знайдемо 15% від 300.
Записуємо коротку умову:
300 – 100%
x – 15% .
Звідси складемо пропорцію:
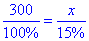або
300:100%=x:15%.
Розв'яжемо пропорцію (добуток крайніх членів = добутку середніх):
300•15%=x•100% звідки
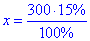
отже x=45.
2) Встановимо, скільки відсотків становить 45 від 180.
Запишемо коротку умову:
180 – 100%
45 – y% .
Звідси складемо пропорцію:
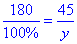
або 180:100%=45:y.
Розв'яжемо пропорцію:
y•180=45•100%, звідки
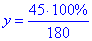
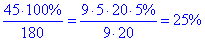
отже y=25%.
Відповідь: 25% – В.
Завдання 2.11 Сплав, маса якого дорівнює 320 кг, містить 20% олова, 144 кг свинцю і решту – домішки. Визначити відсотковий уміст домішок.
Обчислення: 1) Знайдемо відсотковий вміст свинцю у сплаві.
Запишемо коротку умову:
320 г – 100%
144 г – x% .
Звідси мамо:
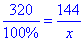
або 320:100%=144:x.
Розв'яжемо пропорцію:
320•x=144•100% звідки
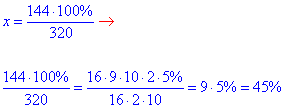
отже x=45%.
2) Знайдемо відсотковий вміст домішок у сплаві:
100%-(20%+45%)=100%-65%=35%.
Відповідь: 35% – В.
Завдання 2.12 Скільки відсотків становить НСД(99; 126) від НСК(12; 20)?
Обчислення: 1) Знайдемо НСД(99; 126).
Розкладемо на множники числа 99 і 126:
99=3•3•11;
126=2•3•3•7.
Отже, НСД(99;126)=3•3=9.
2) Знайдемо НСК(12; 20).
Розкладемо на множники числа 12 і 20:
12=2•2•3,
20=2•2•5.
Отже, НСК(12;20)=2•2•3•5=60.
3) Знайдемо скільки число 9 від числа 60:
Запишемо коротку умову:
60 – 100%
9 – x% .
Звідси складемо пропорцію:
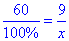
або 60:100=9:x.
Розв'яжемо пропорцію:
60•x=9•100% звідки
, ,
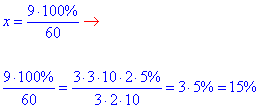отже x=15%.
Відповідь: 15% – В.
Завдання 2.13 Ціна товару була підвищена на 25%.
На скільки відсотків необхідно зменшити нову ціну товару, щоб одержати початкову?
Обчислення: Нехай a - початкова ціна товару, тоді a+0,25a - нова ціна товару.
Складемо рівняння за умовою задачі, де x•100% - зменшення нової ціни:
(а+0.25а)-x(a+0.25a)=a ;
x•1,25=0,25
x=0,25/1,25=0,2.
Отже, x=0,2.
Звідси, 0,2•100%=20%.
Отож, на 20% необхідно зменшити нову ціну товару.
Відповідь: 20% – Г.
Завдання 2.14 Власник клубу має стабільний прибуток. Щоб збільшити прибуток, він підвищив ціну на квитки на 25%. Кількість відвідувачів значно зменшилася, і він вимушений був повернутися до початкової ціни квитка. На скільки відсотків власник клубу зменшив ціну квитка?
Обчислення: Нехай a - початкова ціна квитка, тоді a+0,25 - нова ціна квитка.
Складемо рівняння за умовою задачі, де x•100% - зменшення нової ціни:
(а+0.25а)-x(a+0.25a)=a ;
x•1,25=0,25;
x=0,25/1,25=0,2.
Отже, x=0,2.
Звідси, 0,2•100%=20%.
Отож, на 20% зменшилась ціна квитка.
Відповідь: 20% – Г.
Завдання 2.15 Деяке додатне число спочатку збільшили на 50%, а потім одержане число зменшили на 50%. Як змінилося початкове число?
Обчислення: Нехай a - початкове число, тоді a+0,5a - перше одержане число. (після збільшення числа a на 50%).
Маємо (a+0,5a)-0,5(a+0,5a) - друге число (після зменшення попереднього числа на 50%). Спростимо вираз (a+0,5a)-0,5(a+0,5a):
(a+0,5a)-0,5(a+0,5a) =a-0,25a=0,75a.
Звідси видно, що друге число становить 75% від початкового числа a.
Тому початкове число зменшилось на 100-75=25%.
Відповідь: зменшилося на 25% – Б.
Завдання 2.16 На скільки відсотків збільшиться об'єм куба, якщо його ребро збільшити на 50%?
Обчислення: Нехай a - початкова довжина ребра куба, тоді його об'єм:
V0=a^3.
Ребро куба збільшили на 50%, тобто a+0,5a, тоді V=(a+0,5a)^3.
Спростимо вираз V=(a+0,5a)3:
.
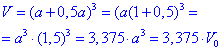Початковий об'єм куба був 1•100%=100%, а кінцевий (після збільшення ребра на 50%) 3,375•100%=337,5%.
Тому, на 337,5% збільшиться об'єм куба, якщо його ребро збільшити на 50%.
Відповідь: на 337,5% – А.
Завдання 2.17 Вкладник вніс до банку 1000 грн. під 8% річних. Яку суму він матиме на рахунку через 3 роки?
Обчислення: Запишемо формулу складних відсотків:
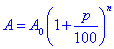
де A0=1000 грн, p=8%, n=3 роки, A, грн.?
Виконаємо обчисення
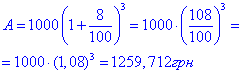
Відповідь: 1000•(1,08) ^3 – Д.
Завдання 2.18 Число a становить 25% числа b. Скільки відсотків становить число b від числа a.
Обчислення: За умовою задачі маємо:
b=25%•a=0,25•a=a/4, тобто b=a/4, звідси a=4b=400%•b.
Тому, число b становить 400% числа a.
Відповідь: 400% – А.
Завдання 2.19 Товар подешевшав на 20%. На скільки відсотків більше можна купити товару за ту ж кількість грошей?
Обчислення: Нехай x - початкова ціна товару,
a0 - кількість товару, яку можна купити за ціну x,
a0•x - початкова кількість грошових витрат, тоді,
x-0,2x - зниження ціни товару на 20%,
a - кількість товару, яку можна купити за ціну (x-0,2x),
a•(x-0,2x) - кількість грошових витрат після зниження ціни.
Але, за умовою задачі грошові витрати залишаються незмінними, тобто
a0•x= a•(x-0,2x),
звідси a0•x= a•(0,8x).
Маємо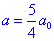
, або a=1,25•a0=125%a0.
Тому 125%-100%=25%.
На 25% більше можна купити товару за ту ж кількість грошей.
Відповідь: 25% – А.
В наступній публікації проаналізуємо задачі на відсотки, що залишилися. Вони відповідають підвищеному рівню складності, тож перед тим як за них братися добре розберіть наведені вище приклади.
