Рівняння з модулями самі по собі не прості, проте коли вони зустрічаються в системах рівнянь то добряче їх ускладнюють внаслідок галуження останніх на декілька варіантів. Далі на готових завданнях із курсу ЗНО підготовки Ви познайомитеся з методами спрощення систем рівнянь, що містять змінні під знаком модуля.
Приклад 20.8 Скільки розв'язків має система рівнянь {|x-3|-y=0; xy-4=0}?
А | Б | В | Г | Д |
Один | два | три | чотири | жодного |
Обчислення: Розв'яжемо систему, що містить рівняння з модулем
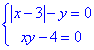
методом підстановки:
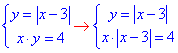
В залежності від знаку виразу х-3, розкриваємо модулі

в підсумку, (4;1) - єдиний розв'язок системи рівнянь (СР).
Відповідь: один – А.
Приклад 20.17 Скільки розв'язків системи рівнянь
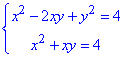
містять нульовий компонент?
А | Б | В | Г | Д |
Один | два | три | чотири | жодного |
Обчислення: Систему рівнянь з двома змінними перетворимо, виділивши в першому рівнянні різницю квадратів
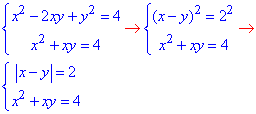
Далі її заміняємо модуль функцією і в залежності від знаку виразу під модулем розбиваємо на дві СР, детальні обчислення яких наведені в таблиці
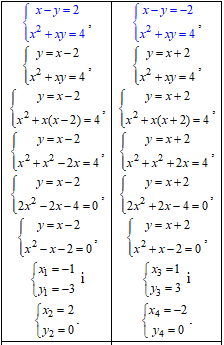
В підсумку маємо (-1;-3), (2;0), (1;3), (-2;0) - 4 розв'язки системи рівнянь.
Серед них є два розв'язки, які містять нульовий компонент, а саме (2;0) і (-2;0). На ЗНО тестах уважно читайте, що потрібно знайти, тому що багато школярів на подібне завдання дають неправильну відповідь (4).
Відповідь: два – Б.
Приклад 20.18 Знайти |x-y|, якщо
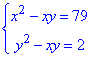
А | Б | В | Г | Д |
8 | 9 | √77 | 7 | 81 |
Обчислення: Додамо обидва рівняння системи та запишемо його першим, в такий спосіб виділимо різницю квадратів, яку далі замінимо рівнянням з модулем:
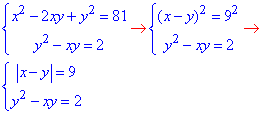
Потрібне в тестах значення ми знайшли |x-y|=9, і на цьому на тестах слід зупинитися.
Розв'яжемо систему рівнянь (не обов'язково):
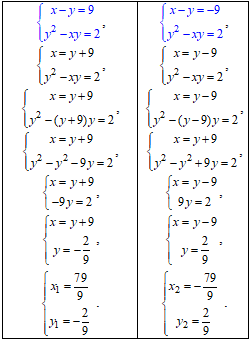
(79/9;-2/9), (-79/9;2/9) - розв'язки заданої системи рівнянь.
Відповідь: 9 – Б.
Приклад 20.19 Скільки розв'язків має система рівнянь
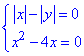 ?
?
А | Б | В | Г | Д |
Один | два | три | більше, ніж три | жодного |
Обчислення: Маємо СР з різницею модулів у першому р-ні. При розкритті рівняння з модулями, отримаємо 4 системи рівнянь, розв'язки яких наведені у таблиці

В підсумку, (0;0), (4;4), (4;-4) - маємо три розв'язки СР.
Відповідь: три – В.
Приклад 20.24 Установити відповідність між системами рівнянь (1–4) та кількістю їх розв'язків (А–Д).

Почнемо з простіших систем, що містять лінійні рівняння. Їх розв'язуємо шляхом виключення однієї зі зімінних у СР, методом додавання рівнянь або підстановки однієї вираженої змінної через іншу.

Приклад 20.28 Установити відповідність між системами рівнянь (1–4) та кількістю їх розв'язків (А–Д).

Маємо 4 системи рівнянь, кожна з яких містить хоча б одне нелінійне рівняння. Перше завдання зводимо до рівняння з модулем, яке отримуємо шляхом представлення правої сторони у вигляді квадрату √6.
Техніки обчислень кожного з варіантів детально розписані у таблиці, тому спробуйте розібрати їх самостійно.

Приклад 20.33 Розв'язати систему рівнянь
{x^2-xy=6, y^2-xy=3}
У відповідь записати найбільшу суму x0+y0, де (x0;y0) - розв'язок системи.
Обчислення: Маємо систему нелінійних рівнянь, кожне з яких в лівій його частині містить частину формули різниці квадратів
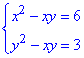
Додамо обидва рівняння і запишемо як перше рівняння системи:
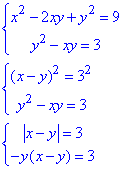
В такий спосіб перейдемо до рівняння з модулем, яке розкриваємо в залежності від знаку виразу під модулем
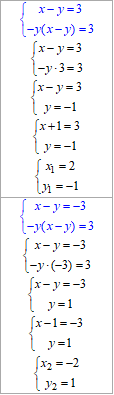
Отримали 2 розв'язки системи рівнянь (2;-1) і (-2;1), вибираємо першу пару, щоб отримати найбільшу суму компонентів
x0+y0=2+(-1)=1.
Відповідь: 1.
На цьому один урок із ЗНО підготовки добігає кінця, більше нових готових прикладів на СР Ви знайдете на сусідніх сторінках сайту та онлайн. Практикуйте і нехай у Вас виходять лише правильні відповіді!


