Розв'язування логарифмічних та показникових виразів

У шкільній програмі логарифи та властивості показникових функцій добре вивчають в 10, 11 класі. Далі учнів чекають ЗНО тести та вступ у ВУЗи. Онлайн курсів ЗНО досить багато, як і готових розв'язків по цій темі прикладів. Одні досить прості і не містять розширених пояснень, інші навпаки – мають все гарно розписано, але на простих прикладах. Ми ж намагаємося Вам дати максимум, що можна перечитати і розібрати за один раз, більшість статей учні не можуть освоїти з першого разу, тому приходять до нас повторно. Далі залишаються та використовують сайт в навчанні в шкільні роки та при здобутті вищої освіти.
Усі базові формули до теми ми виписали в першій статті, тож якщо буде важко розбирати відповіді починайте з початків.

Приклад 6.30 Установити відповідність між виразами (1–4) та їхніми значеннями (А–Д).


Розв'язування: Заданий тип логарифмів спрощують методом перетворення чисел в логарифмах чисельнику до тих, що містяться в логарифмах у знаменнику.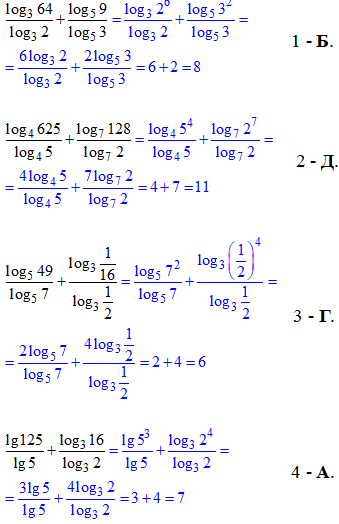

Обчислення не складні і нам дещо дивно, як такі завдання на ЗНО тестах йдуть одні з останніх та за їх обчислення нараховують високі оцінки.

Приклад 6.31 Установити відповідність між виразами (1–4) та їхніми значеннями (А–Д).

Розв'язування: Маємо 4 варіанти тесту, в кожному завданні є добутки логарифмів в яких попарно основа другого логарифма є числом першого логарифма в певному показнику, і число другого в другому логарифмі рівне основі першого в певному степені.
Тому спершу працюємо з показниками, а далі пригадуємо співвідношення для переходу до іншої основи в логарифмі:
log_ab=1/log_ba.
Знаючи цю властивість логарифма без проблем виконуємо наступні обчислення:

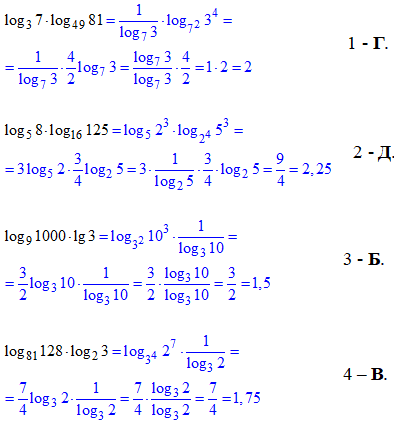
Приклад 6.32 Установити відповідність між виразами (1–4) та їхніми значеннями (А–Д).

Розв'язування: Необхідно спростити добутки трьох логарифмів з різними основами. Для цього в другому та третьому логарифмі переходимо до основи першого логарифма, і так для всіх 4 завдань тесту.
Алгоритм застосовуйте для спрощення усіх завдань де задані добутки логарифмів з не рівними між собою основами.

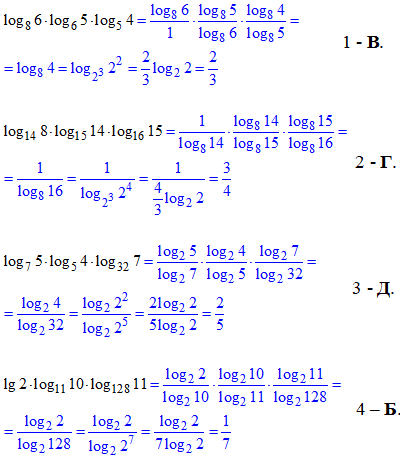
Приклад 6.33 log₇2=a, log₇3=b. Установити відповідність між логарифмами чисел (1–4) та їх вираженням через a та b (А–Д).

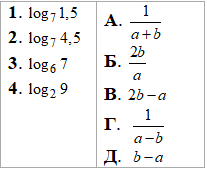
Розв'язування: Спрощуємо вирази за допомогою формул суми логарифмів та різниці:

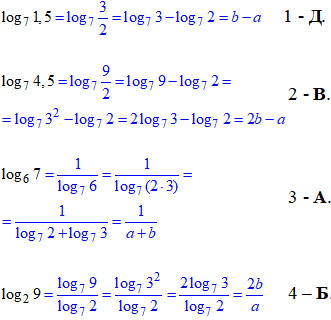
Наведені приклади на практиці є повторенням найпоширеніших властивостей логарифма, вчіть їх із запропонованих пояснень.

Приклад 6.34 log_ab=5. Установити відповідність між виразами (1–4) та їхніми значеннями (А–Д).

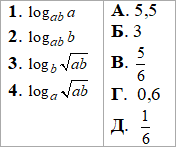
Розв'язування: Тестові завдання на перетворення виразів виконуємо за допомогую правила переходу до другої основи під логарифмом
log_ab=log_сb/log_сa
та розписання логарифму добутку через суму логарифмів
log_a(b·c)=log_ab+log_ac.
Детально перетворення наведені далі

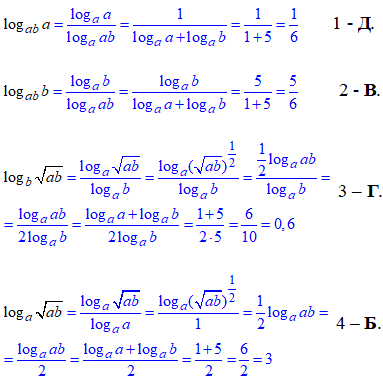
Приклад 6.35 Обчислити значення виразу
1/70•2^(3log27).
Розв'язування: Використаємо основну логарифмічна тотожність

решта обчислень зводиться до піднесення сімки до кубу та множення на дріб =1/70:
 
Відповідь: 4,9.

Приклад 6.36 Обчислити:
25^(2-log₅75)+7^(-log₇3)•27.
Розв'язування: Розписуємо степені та зводимо під застосування основної логаріфмічної тотожності
.
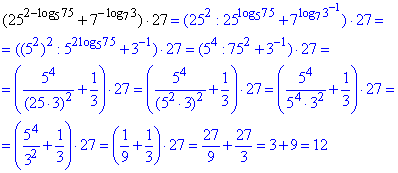Відповідь: 12.

Приклад 6.37 Обчислити:
3^(log35/log53)-5^log35+7^log749.
Розв'язування: Завдання виконуємо кілька разів застосовуючи основну логарифмічну тотожність
.
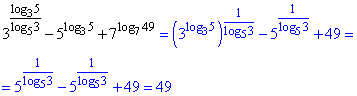Відповідь: 49.

Приклад 6.40 Обчислити значення виразу:

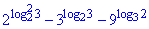
Розв'язування: Маємо різницю показникових виразів де в степені задані логарифми.
Для спрощення виразу спершу скористаємося властивостями показникових функцій та розпишемо логарифми так, щоб можна було застосувати основну логарифмічну тотожність

В результаті отримаємо:
 
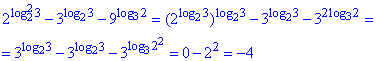
Відповідь: -4.

Приклад 6.43 Обчислити значення виразу
log_a500-loga4, якщо log₅a=1/4.
Розв'язування: Просте, на нашу думку, завдання на формулу різниці логарифмів + застосування переходу від однієї основи під логарифмом до іншої:

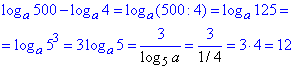
З такого плану завданнями на перетворення логарифмів  Ви повинні вміти виконувати на відмінно. Лише тоді зможете розраховувати на високі оцінки та правильні результати.
Відповідь: 12.

На цьому розгляд готових тестів із ЗНО підготовки не завершено, попереду Вас чекають схеми обчислень більш складніших вправ.