Готові приклади на системи рівнянь, що містять логарифми підібрано із ЗНО тестів. Для обчислення завдань необхідно добре знати властивості логарифма. Також при обчисленнях слід враховувати область допустимих значень (ОДЗ), якщо цього не робити, то розв'язки слід перевіряти на правильність підстановкою.
Приклад 20.11 Розв'язати систему рівнянь {lg(x+y)=2, lg(x-y)=1} і вказати компонент y0 її розв'язку (x0;y0).
А | Б | В | Г | Д |
35 | 110 | 90 | 55 | 45 |
Обчислення: Маємо систему логарифмічних рівнянь
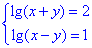
тому спершу виписуємо обмеження на логарифми.
ОДЗ: {x+y>0, x-y>0}
Далі, за властивістю логарифма logaa=1, перетворюємо праві сторони рівнянь та розкриваємо логарифми
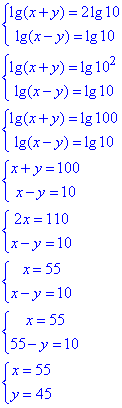
Значення (55;45) є розв'язком системи рівнянь з логарифмами, звідси y0=45 – другий компонент розв'язку системи.
Відповідь: 45 – Д.
Приклад 20.12 Знайти суму компонентів розв'язку системи рівнянь 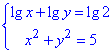
А | Б | В | Г | Д |
-3 | 3 | √7 | 9 | 7 |
Обчислення: Запишемо ОДЗ логарифмів: {x>0,y>0}.
Суму логарифмів, за властивістю logab+logac=loga(b·c), замінюємо логарифмом добутку.
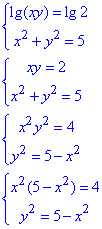
Розв'яжемо перше рівняння, для цього біквадратне рівняння зведемо до квадратного заміною змінних x^2=t. Далі, після розв'язання, повернемося до заміни і знайдемо "ікси", останнім кроком підставимо "ікси" в друге рівняння системи, та знайдемо "ігрики".

Дістали (1;2), (2;1) -два розв'язки системи рівнянь.
Сума їх компонентів рівна
1+2=3.
Відповідь: 3 – Б.
Даний приклад можна розв'язати графічним методом. Для цього після розкриття логарифма систему {x2y2=4, y2=5-x2} замінити системою функцій y(x):
{y=2/x, y=√(5-x)2}.
Далі побудуємо графік кола та оберненої функції в Мaple
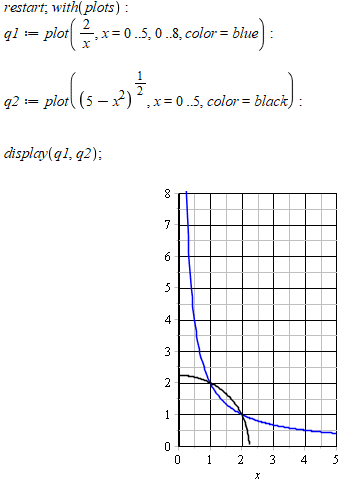
Як можна переконатися, точки перетину кривих спвпадають зі знайденими раніше.
Приклад 20.36 Розв'язати систему рівнянь
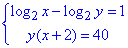
У відповідь записати найбільшу суму x0+y0, де (x0;y0) - розв'язок системи.
Обчислення: Перше рівняння системи містить різницю логарифмів, її, за властивістю, заміняємо логарифмом частки. Одиницю в правй сторні запишемо як логарифм основи. В такий спосіб можеме опустити логарифми та перейти до розгляду виразів під логарифмами.
ОДЗ логарифмів: {x>0;y>0}.
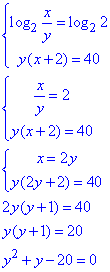
За теоремою Вієта маємо y1=4,
y2=-5<0 (не належить ОДЗ).
Знаходимо "ікс"
x=2•4=8.
(8;4) - єдиний розв'язок системи рівнянь, обчислимо суму
x0+y0=8+4=12.
Відповідь: 12.
Приклад 20.38 Розв'язати систему рівнянь
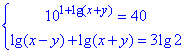
У відповідь записати найбільшу суму x0+y0, де (x0;y0) - розв'язок системи.
Обчислення: Випишемо ОДЗ логарифмів:
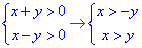
Далі спростимо рівняння, при цьому повторимо властивості показникових та логарифмічних функцій
(уважно перегляньте пояснення)
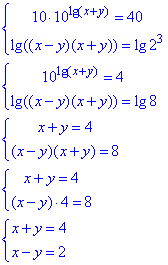
Додамо обидва рівняння:
2x=6,
x=3.
3+y=4,
y=1.
(3;1) - розв'язок системи рівнянь, тому x0+y0=3+1=4 - найбільша сума.
Відповідь: 4.
Приклад 20.43 Розв'язати систему рівнянь
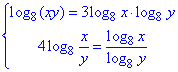
У відповідь записати найбільшу суму 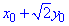 , де (x0;y0) - розв'язок системи.
, де (x0;y0) - розв'язок системи.
Обчислення: Виписуємо ОДЗ функцій:
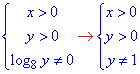
Робимо заміну:
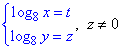
тоді, за властивостями логарифма, систему рівнянь заміняємо еквівалентною, та розписуємо до квадратного р-ня
(проміжні перетворення виконайте самостійно, або з'ясуйте чому так?)
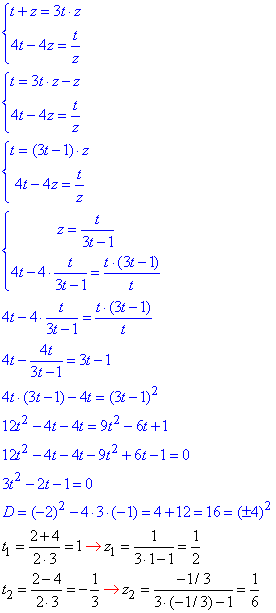
Повернемося до заміни та знайдемо x,y з системи логарифмічних рівнянь:
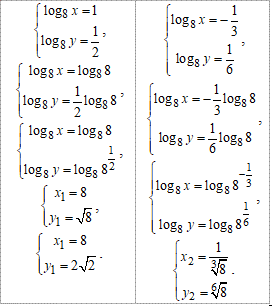
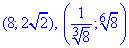 - розв'язки заданої системи рівнянь, тому
- розв'язки заданої системи рівнянь, тому
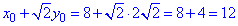 - найбільша сума.
- найбільша сума.
Відповідь: 12.
Хоча прикладів не багато, проте всю складність, що Вас чекає в подальшому навчанні Ви побачили в повній мірі. Вчіть властивості логарифмів, практикуйте побільше самостійно, інакше отримаєте фіаско на практичних.
Ми зі своєї сторони будемо постійно доповнювати статті сайту новими прикладами, щоб навчити Вас розв'язувати дедалі більше завдань зі шкільного курсу та ВУЗів.


