Складні показникові нерівності зі ЗНО

Всі хто вперше зайшов на сайт думають, ну що може буте складного в показникових нерівностях, ми ж багато таких сайтів переглянули і всюди одні та ті ж завдання. Та дочитайте пояснення до кінця, перегляньте формули спрощення показникових виразів, схеми розкриття показникових нерівностей і дайте об'єктивну оцінку, чи самостійно Ви б змогли розв'язати наведені нерівності.

Приклад 15.26 Розв'язати нерівність

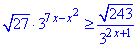
У відповідь записати суму всіх цілих розв'язків нерівності.
Розв'язування: Маємо кілька коренів квадратних, які бачимо, що потрібно зводити до степенів трійки. Групуємо множники з "іксами" по одну сторону нерівності, а сталі переносимо в іншу

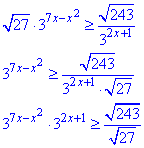
Зауважимо, що √27>0 і 3^2x+1>0 для всіх x, тому ділення і множення обох частин нерівності на ці вирази не міняє знаку нерівності.
Перетворюємо далі вирази до тих пір, поки не отримаємо зліва та справа спільної основи =3

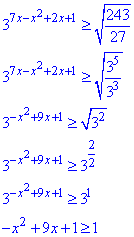
При опусканні основ і прирівнюванні степенів знак нерівності не змінили, оскільки основа більша одиниці 3>1.

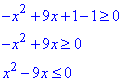
В останній формулі знак нерівності змінили на протилежний, тому що обидві частини нерівності множили на -1, від'ємне число.
Квадратичну нерівність, що отримали, розв'язуємо методом інтервалів
x(x-9)≤0
x(x-9)=0
x₁=0 і x₂=9.

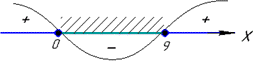
звідси x∈[0;9].
Випишемо усі цілі розв'язки та знайдемо їх суму:
0; 1; 2; 3; 4; 5; 6; 7; 8; 9.
1+2+3+4+5+6+7+8+9=45.
Відповідь:45.

Приклад 15.32 Розв'язати нерівність

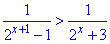
У відповідь записати координату середини проміжку, який є розв'язком нерівності.
Розв'язування: Вирази в знаменнику не повинні перетворюватися в нуль, звідси розписуємо два рівняння для ОДЗ:

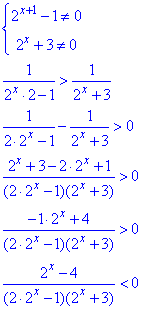
Обидві частини нерівності помножили на -1, тому знак нерівності змінили на протилежний.
(2^x-4)(2•2^x-1)(2^x+3)<0.
(ОДЗ у цій нерівності вже враховано).
Вираз 2^x+3>0 додатний для всіх x, тому на розв'язок заданої нерівності не впливає, його відкидаємо
Кінцеву нерівність заміною 2^x=t>0 зводимо до квадратної, хоча методом інтервалів можна і не переходити до замін, а одразу шукати корені відповідного рівняння і розставляти знаки на інтервалах
(2^x-4)(2•2^x-1)<0,
(2^x-4)(2•2^x-1)=0.
Розпишемо рівняння та побудуємо числову вісь з проміжками знакосталості

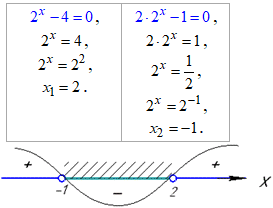
Інтервал (1;2) – є розв'язком нерівності.
Запишемо координату середини проміжку
(-1+2)/2=0,5.
Відповідь:0,5.

Приклад 15.36 Розв'язати нерівність 3^x²+2-5^x²-1>5^(x²+1)+3^(x²-1).
У відповідь записати суму всіх розв'язків нерівності.
Розв'язування: Маємо пари показникових виразів по різні сторони від знаку >, тому попередньо переносимо вирази з основою 3 в одну сторону, з 5 в іншу. Далі виносимо показникові вирази в меншім степені за дужки та групуємо, що залишилося.

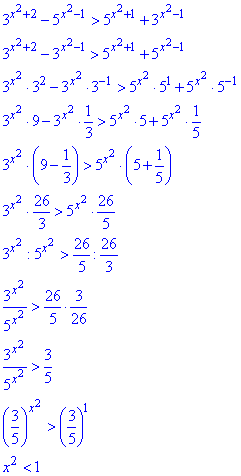
Степені отримали рівні, тому можемо перехресно розділити вирази та перейти до нерівності з основою 3/5.
Зауважуємо, що основа 3/5<1, тому порівнюючи степені знак змінюємо на протилежний.
x²-1<0
(x+1)(x-1)<0.
Методом інтервалів визначаємо корені нерівності
(x+1)(x-1)=0,
x1=-1, x2=1.

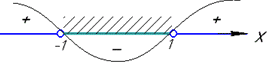
x∈(-1;1).
Оскільки розв'язками є взаємно протилежні числа на проміжку від -1 до 1, то їх сума дорівнює 0.
В іншому випадку, ми б суму не знайшли, хіба що окремо цілих або натуральних чисел.
Відповідь:0.

Приклад 15.38 Розв'язати нерівність (1/4)^{2x-0,5x^2}≥2^|2x-10|+x.
У відповідь записати суму всіх цілих чисел, які не є розв'язками нерівності.
Розв'язування: Наберіться терпіння, тому що переходимо до найважчих завдань ОДЗ підготовки, а це значить що обчислень буде багатенько.
Спершу перетворюємо вираз, щоб всюди мати в основі двійку. Далі опускаємо основи та прирівнюємо степені, тому в нерівності з однієї сторони матимемо модуль, з іншої квадратичну залежність. Розкриваємо модуль та заміняємо системою двох нерівностей.
З текстового пояснення Ви мало що зрозумієте, тому краще розберіть всі переходи з наступних формул

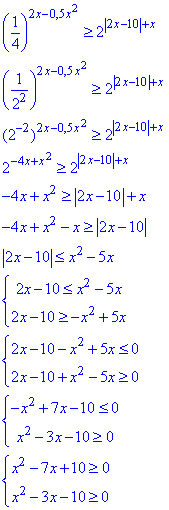
Методом інтервалів випишемо спільні розв'язки системи нерівностей:

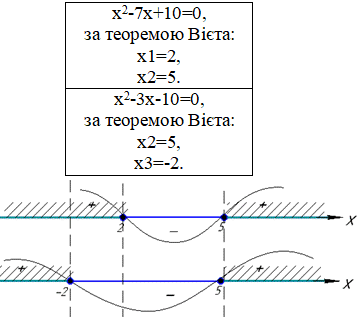
x∈(-∞;-2]∪[5;+∞) – розв'язок.
Випишемо усі цілі числа, які не є розв'язками та знайдемо їх суму:
-1; 0; 1; 2; 3; 4.
-1+1+2+3+4=9.
Відповідь:9.

Приклад 15.40 Розв'язати нерівність

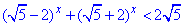
У відповідь записати суму всіх розв'язків нерівності.
Розв'язування: За формулою різниці квадратів перетворимо вираз √5-2:

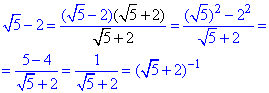
Щоб спростити нерівність перемножимо її на вираз (√5+2)^x:

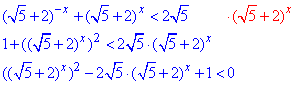
Заміною: (√5+2)^x=t, де t>0, зводимо вихідну нерівність до квадратичної:
t²-2√5t+1<0.
Останню розв'язуємо через корені квадратного рівняння


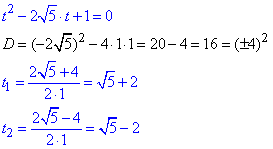
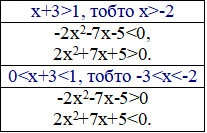
звідси t∈(√5-2;√5+2).
Повертаємося до заміни та розв'язуємо нерівність


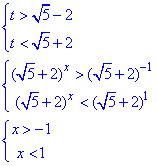
Нерівність справедлива на інтервалі x∈(-1;1).
Бачимо, що розв'язками показникової нерівності є протилежні за знаком числа з інтервалу (-1;1), тому їх сума рівна нулю.
Відповідь:0.

Приклад 15.41 Розв'язати нерівність (x+3)^(-2x²-7x-5)<1.
У відповідь записати суму всіх цілих недодатних розв'язків нерівності.
Розв'язування: Випишемо ОДЗ для показникової функції:

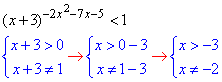
Останні дві умови слід далі врахувати, саме для того ОДЗ і виписуємо.
За властивістю одиницю заміняємо основою в нульовому степені
(x+3)^{-2x^2-7x-5}<(x+3)
Щоб розкрити нерівність треба знати основу, а в нас вона поки що невідома.
Тому спершу прирівняємо показники та знайдемо нулі квадратного рівняння

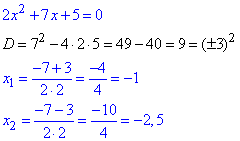
Методом інтервалів об'єднаємо розв'язки обох останніх нерівностей, врахувавши ОДЗ:

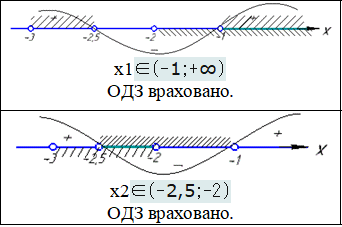
x∈(-2,5;-2)∪(-1;+∞).
Випишемо усі цілі недодатні числа, які є розв'язками нерівності та знайдемо їх суму:
умові відповідає єдине значення 0 (нуль).
Відповідь: 0.

Як бачите, не такі тривіальні показникові нерівності розібрали, як Ви, мабуть, чекали. Попереду як важчі, так і легші приклади з курсу ЗНО підготовки, так що перелистуйте сторінку і вперед до нових показникових нерівностей.