Системи рівнянь з параметром

Розв'язувати прості системи рівнянь з параметром Вас починають вчити в шкільному курсі алгебри в 10-11 класі, а далі на складніших завданнях у ВУЗ-ах. Наведені готові приклади взято із програми ЗНО підготовки з математики, яка містить понад 40 прикладів як на лінійні, так і показникові та логарифмічні рівняння, а також з модулями. Переглядайте та беріть для себе кращі способи розкриття систем рівнянь.

Приклад 20.14 За якого значення a система рівнянь {2x-y=5; x+ay=2} не має розв'язків?

Обчислення: Систему рівнянь з двома невідомими розв'язуємо додаванням рівнянь, попередньо домноживши друге на -2:

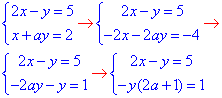
Далі аналізуємо рівняння і приходимо до висновку, що система рівнянь не має розв'язку, якщо вираз в дужках рівний нулю
2a+1=0.
2a=-1,
a=-1:2=-0,5.
Відповідь: -0,5 – Б.

Приклад 20.15 За якого значення a система рівнянь {3x+y=-15;-x-ay=5} має безліч розв'язків?

Обчислення: Перетворимо систему рівнянь з параметром, щоб позбутись однієї змінної

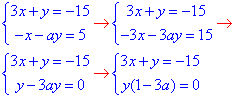
З другого рівняння зауважуємо, що система рівнянь має безліч розв'язків, якщо 1-3a=0.
Знаходимо параметр
-3a=-1,
a=1/3.
Відповідь: 1/3 – А.

Приклад 20.16 За яких значень a і b система рівнянь {6x+b·y=5a, 5a·x-6y=b} має розв'язок (-1;2)?

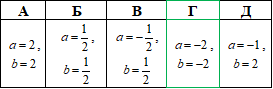
Обчислення: Маємо систему двох лінійних рівнянь 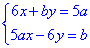, яка описує прямі на площині. Точка з умови за фізичним змістом є точкою перетину цих прямих, залишилося підставити її координати в СР та знайти з останньої два невідомі параметри a і b

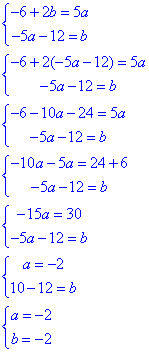
Обчислення не важкі, в чому можете переконатися з наведених вище формул.
Відповідь: a=-2, b=-2 – Г.

Приклад 20.13 Яка з наведених систем за будь-яких значень параметра p має єдиний розв'язок?

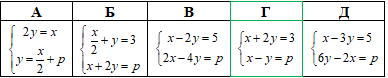
Обчислення: В ЗНО тестах маємо 5 СР з параметром, обчислюємо кожну та визначаємо, яка з систем має один розв'язок.
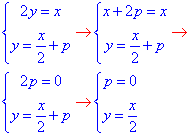- система має безліч розв'язків при p=0;

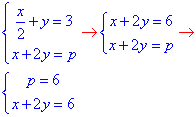-  система має безліч розв'язків, якщо p=6;

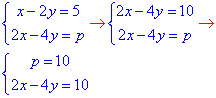- СР має безліч розв'язків при p=10;

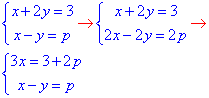- система має єдиний розв'язок за будь-яких значень p;

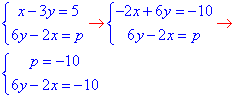- СР має безліч розв'язків при p=-10.

Відповідь: {x+2y=3; x-y=p} – Г.

Приклад 20.20 За якого значення a система рівнянь {x²+y²=4, x-y=a} має єдиний розв'язок?

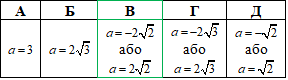
Обчислення: Перше рівняння описує коло радіусом 2 з центром у початку координат, друга пряму.
Перетворимо СР

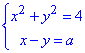
шляхом вираження невідомої з другого рівняння і підстановкою в перше

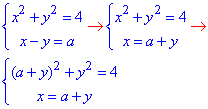
Розв'яжемо 1 рівняння, розписавши до квадратного, а далі через дискримінант

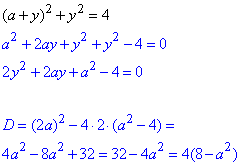
Квадратне рівняння, а відтак і система рівнянь, має єдиний розв'язок, якщо дискримінант рівний нулю D=0:
звідси маємо умову для обчислення параметра

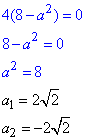
Відповідь: a=-2√2 або a=2√2 – В.

Приклад 20.22 За якого значення k пряма y=kx+2 проходить через точку перетину прямих x+y=5 і x-y=1?

Обчислення: Знайдемо точку перетину прямих x+y=5 і x-y=1.
Для цього складемо систему рівнянь з рівнянь прямих і розв'яжемо її (методом додавання):

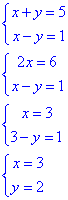
Отримали точку (3;2). Підставимо її (3;2) у рівняння y=kx+2 і знайдемо значення кутового коефіцієнта прямої k:
2=3k+2,
3k=0,
k=0.
Цей випадок відповідає прямій, паралельній осі абсцис y=2.
Відповідь: 0 – В.

Приклад 20.23 За якого значення a система рівнянь

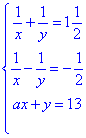
має розв'язок?

Обчислення: ОДЗ: {x≠0;y≠0}.
Спочатку розв'яжемо систему перших двох рівнянь (методом додавання):

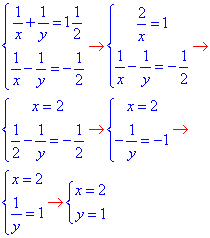
(2;1) - розв'язок СР.
Підставимо {x=2;y=1} у рівняння з параметром ax+y=13 і розв'яжемо:
2a+1=13,
2a=12,
a=6.
При a=6 система рівнянь має розв'язок і він рівний (2;1).
Відповідь: 6 – Д.

Приклад 20.30 Вказати значення параметра a, за якого система {ax+3y=9;12x+ay=18} має безліч розв'язків.
Обчислення: Перегляньте уважно наведену схему обчислення системи рівнянь. В штучний спосіб виразили одну зі змінних через параметр

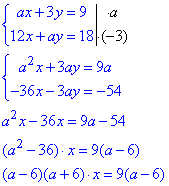
Рівняння, а відтак, і задана СР має безліч розв'язків, якщо вираз рівний нулю
a-6=0,
a=6.
В підсумку: при a=-6 система рівнянь розв'язків не має, а при a=6 СР має єдиний розв'язок.
Відповідь: 6.

Приклад 20.44 За якого значення a сума x+y набуває найменшого значення, якщо
?
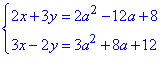Обчислення: Домножимо перше рівняння на 2, друге на 3

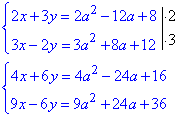
та додамо, щоб позбутися y
13x=13a²+52,
x=a²+4.
Підставимо отримане значення x у перше рівняння системи і знайдемо y: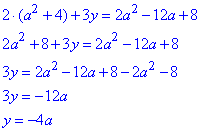

Отримали (a²+4;-4a) - розв'язок системи рівнянь за будь-якого значення a. Складемо суму x+y:

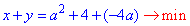
Запишемо функцію:

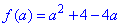
Вона приймає мінімальне або максимальне значення в точці, де похідна рівна нулю.
Обчислимої похідну:

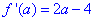
та прирівняємо її до нуля, щоб знайти критичні точки:
2a-4=0,
2a=4,
a=2.
При a<2 похідна f'(a)<0, тому функція f(a) спадає, при a>2 похідна f'(a)>0, тому функція f(a) зростає. Отже, a=2 - точка локального мінімуму, а тому сума x+y буде найменшою, і рівною
x+y=2²+4-4·2=0.
Відповідь: 2.

Вплив параметра на розв'язок СР має важливе значення в задачах на оптимізацію, в економічних задачах, та ряді прикладних наук. Схеми обчислення прикладів із ЗНО тестів ми Вам тут привели, реальні системи рівнянь з параметрами набагато складніші і доволі часто їх доводиться обчислювати числовими чи графічними методами. Тому більше практикуйте самостійно з подібними завданнями та не майте труднощів на практичних!