Складні логарифми та показникові вирази

Залишилися розв'язати складні приклади на логарифми та степені, і ми зараз з Вами пепеглянемо як такі вирази спрощувати. Перед переглядом готових відповідей рекомендуємо почитати усі попередні онлайн уроки із курсу ЗНО підготовки, вони містять більше пояснень як застосовувати властивості логарифмів та показникових функцій на простіших (їх 37) в плані обчислень завданнях. Думаю, у Вас вистачить знань з теорії та бажання, щоб прочитати розрахункові формули без допомоги.

Приклад 6.38 Із застосування основних формул для степенів та логарифмів отримаємо:

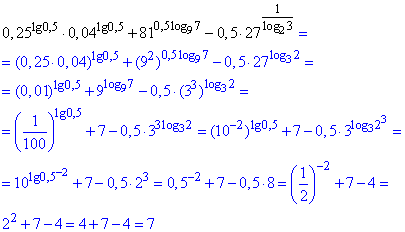
Без знання властивостей логарифма Ви в навчанні далеко не просунетеся, наведені приклади Ви ще зможете прочитати, а от повторити обчислення не всім буде легко. Тому вчіть усі формули, що виділені в поясненнях до прикладів.
Відповідь: 7.

Приклад 6.39 Обчислити: log₃49•log_√75•log₂₅27.
Розв'язування: Розрахунок виконуємо за допомогою формул винесення показника з основи логарифма та самого логарифма
log_ab^k=k•log_ab,
log_a^pb=1/p•log_ab.
Після цього застосовуємо співвідношення для переходу від однієї основи до іншої
log_ab=log_сa/log_cb.
Решта обчислень зводяться до спрощення однакових логарифмів та множення дробів:

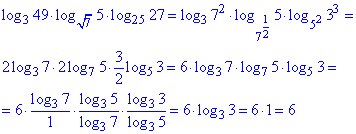
Відповідь: 6.

Приклад 6.41 Обчислити:

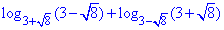
Розв'язування: Маємо суму логарифмів, в яких в основі та під логарифмом містяться вирази з коренями, причому спадає на думку формула різниці квадратів.
Тому її використаємо для перетворення виразу 3-√8:

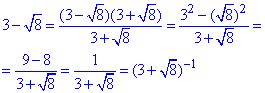
Враховуючи отриманий запис, розписуємо логарифми та обчислюємо їх суму:

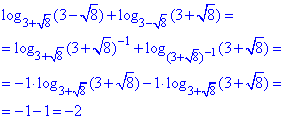
Відповідь: -2.

Приклад 6.42  Обчислення громіздкі, проте в формулі є усі пояснення, що і для чого поетапно виконували.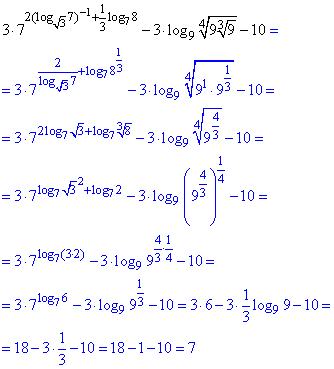

Учіться читати відповіді до таких завдань, заодно запам'ятовуйте формули перетворень.
Відповідь: 7.

Приклад 6.44 Дано: log_aba=9. Знайти log_abb.
Розв'язування: Щоб спростити вираз треба застосувати штучний прийом, який полягає в тому, щоб справа та зліва відняти одиницю.
В подальшому її замінюємо логарифмом основи в першій частині, що згодом дозволяє знайти різницю логарифмів 
log_ab-log_aс= log_a(b/с)
яка за правилом віднімання рівна логарифму частки виразів.
В результаті обчислень отримаємо шукане значення log_abb з множником рівним (-1), яку переносимо за знак рівності.

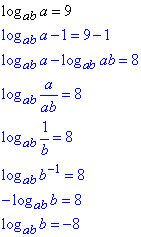
Відповідь: -8.

Приклад 6.45 Спростити вираз

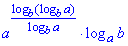
Розв'язування: В показнику маємо частку логарифмів з однаковою основою, але чисельник в додаток містить вложений логарифм. Щоб його розкрити потрібно застосувати правило зміни основи під логарифмом
.
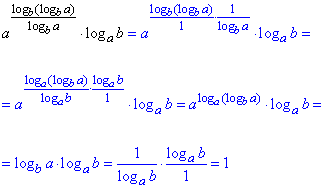Відповідь: 1.

Приклад 6.46 Знайти:
(log₅2+log₂5+2)(log₅2-lg2)•log₂5-log₅2.
Розв'язування: Обчислення досить складні, щоб Ви розібралися з роз'ясненнями чому саме в такому порядку перетворювали логарифми.
Маємо добуток виразів з логарифмами, і зрозуміло, що одна з дужок повинна дати вклад в спрощення розразунку.
Починаємо з другої дужки, застосовуючи зміну основи під логарифмами, формули для цього наступні:
log_ab=log_сa/log_сa;
log_ab=log_ba.
Ми повторюємо виписувати формули логаривмів у кожному завданні, щоб Ви не гортали сторінку та бачили в якому контексті їх застосовувати.

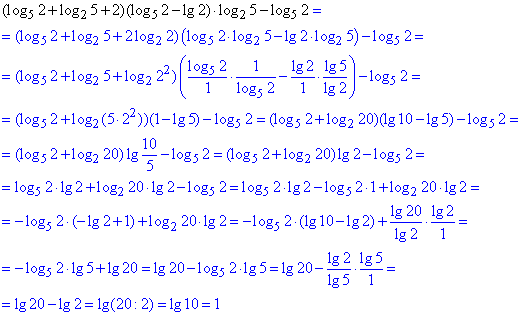
Розписування зайняло багато часу та місця, в шкільній практиці такі завдання не задають, у ВУЗах будьте готові що Вам зададуть як простіші завдання, так і складні.
Відповідь: 1.

Приклад 6.47 Відомо, що log₄₉x=2log₄₉6+log₄₉12+log₄₉15 і y=45^(1+log₄₅2).

Знайти:
1. log₂(x/y);
2. (x+y)^0,5/√15.

Розв'язування: Спростимо праву частину виразу log₄₉x=…:

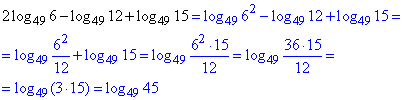
Знайдемо x:
log₄₉x=log₄₉45, звідси x=45.
За властивостями додавання показників розпишемо вираз 45^(1+log₄₅2) та зведемо під основну логарифмічну тотожність:

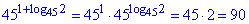
Ззвідси y=45•2=90.

Далі виконуємо підстановку знайдених значень в умову та спрощуємо логарифм
1)
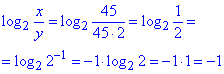
та корінь квадратний з суми змінних x+y
2)
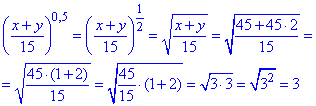
Сама підстановка не важка, лише відшукання невідомих вимагає уважності та знання правил.
Відповідь: 1) -1; 2) 3.

Приклад 6.48 Якщо log_ab=5, то

• 1) log_b√(ab);
• 2) log_a√(ab).

Розв'язування: В обидвох пунктах тестів слід застосувати властивості логарифма:
в першому прикладі переходимо до основи a під логарифмом

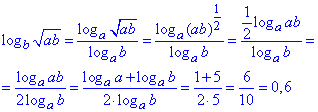
В другому прикладі добуток параметрів під коренем подамо у степеневіій формі та винесемо степінь з під логарифма

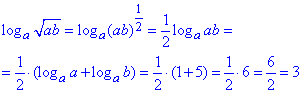
Далі під логарифмом дістанемо добуток, який розписуємо через суму логарифмів.
Зауважуємо, що один з них рівний одиниці, оскільки містить логарифм основи.
Відповідь: 1) 0; 2) 3.

Дякуємо усім хто займається самопідготовкою та регулярно використовує матеріали сайту в навчанні.
Розв'язуйте побільше подібних прикладів, виписуйте та вчіть формули, розширюйте наявний багаж знань.
Пам'ятайте, зараз інформації багато, головне вміти і хотіти її відфільтровувати.
Кожна потрачена година віддана на освіту рано чи пізно окупиться!