"Решить уравнение с модулями" или "Найти решения уравнения с модулем" – одни из самых популярных заданий в школьном курсе математики, у многих на первом курсе в ВУЗах при изучении модулей. Примеры легко сводятся к обычным уравнениям при знании правил - а они достаточно просты. При раскрытии модуля требуется найти точки в которых подмодульная функция принимает нулевое значение. Истинную ось разбить найденными точками на интервалы и установить знаки функции на каждом из них. Дальше раскрывают модули по правилу:
Если подмодульная функция положительная то модули раскрывают без изменений. Если отрицательная то раскрывая модуль функцию берут со знаком минус.
Все это напрямую следует из определения модуля числа:
![]()
После вычислений проверяют принадлежит найденное решение рассматриваемому интервалу или нет. Таким образом отсеивают лишние результаты.
Для наглядности перейдем к вычислениям .
Пример 1. Найти решение уравнения
![]()
Решение:
Этот пример является простейшим типом уравнений с модулями. В первую очередь уравнение содержит модуль один раз и переменная входит линейно.
Находим точку в которой выражение под знаком модуля обращается в нуль
![]()
Справа от этой точки выражение под модулем принимает положительное значение, слева - отрицательное.
Раскрывая модуль получим два уравнения с условиями на неизвестную
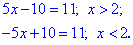
Находим решения уравнения
![]()
![]()
Такого типа уравнение с модулем можно решить графическим методом. В результате получим следующий вид функций
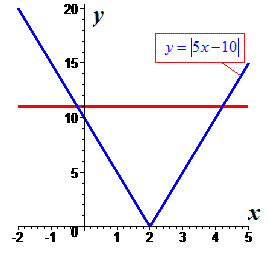
Пример 2. Найти решение уравнения
![]()
Решение: Решаем по схеме предыдущего примера.
Находим точки в которых модули превращаются в ноль.
![]()
![]()
Обе точки разделяют действительную ось на интервалы.
![]()
Обозначаем знаки подмодульных функций на найденных интервалах. Знаки устанавливаем простой подстановкой точек из интервала
![]()
![]()
![]()
Для удобства можете обозначать интервалы графически, некоторым это очень помогает, но можно обойтись только приведенными выше записями.
Раскрываем модули учитывая знаки и находим решения.
![]()
![]()
![]()
Последнее решение не имеет смысла, поскольку не принадлежит промежутку на котором его находим. Таким образом уравнения удовлетворяют значения
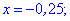
![]()
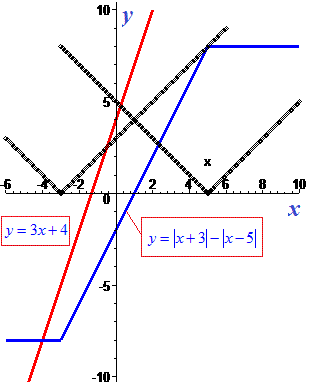
Графики модуль-функций приведены ниже, точки их пересечения и являются решением.
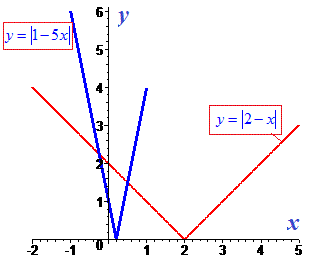
Пример 3.Найти решение уравнения
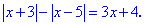
Решение: Находим точки, которые разбивают ось на области знакопостоянства
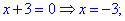
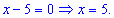
Определяем знаки подмодульных функций на этих областях
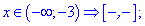
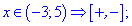
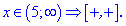
Раскрываем модули и вычисляем
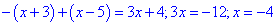
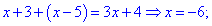
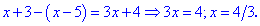
Второе и третье значение не принадлежат области, следовательно уравнению отвечает только x=-4.
Ниже модули изображены графически
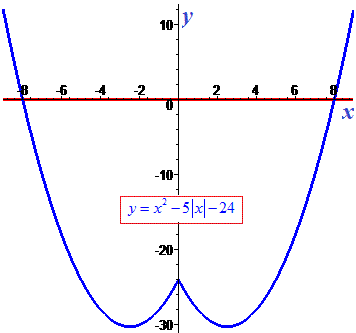
Пример 4. Найти решение уравнения
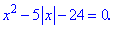
Решение: Есть квадратный трехчлен который сводится к решению двух уравнений
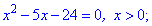
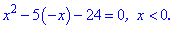
Решаем каждое из квадратных уравнений . Дискриминант у них будет одинаковый
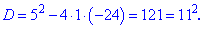
Находим корни первого уравнения
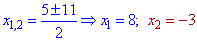
и второго
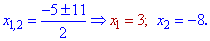
Обозначенные корни уравнения не относятся области на которой искали решение. Окончательно получим
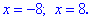
На графике модуль-функции решение является пересечением с осью Ox
Пример 5. Решить модульное уравнения
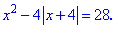
Решение:Точка x=-4 делит область на интервалы
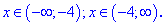
На первом интервале получим квадратное уравнение
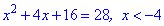
на втором соответственно следующее
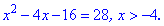
Вычисляем дискриминант первого
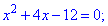
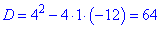
и корни
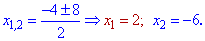
Второе уравнение будет иметь решения
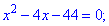
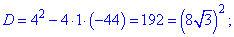
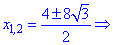
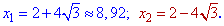
Два корня отпадают, а два являются решениями
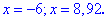
График функции с модулем вместе с точками пересечения иллюстрирует следующий рисунок
Пример 6. Решить модульное уравнения
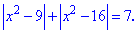
Решение:Схема решения предыдущая . Находим нули
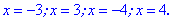
Делим область на пять интервалов в которых находим знаки функций
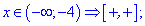
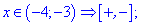
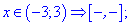
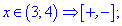
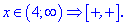
Раскроем модули для первой и пятой областей
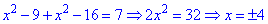
Данные точки принадлежат краю области, однако при подстановке уравнение превращается в тождество.
Второй интервал
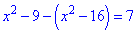
превращается в тождество, следовательно все точки интервала включая краями являются решениями.
Третий интервал
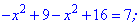
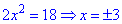
дает два корня , которые удовлетворяют исходное уравнение с модулями.
На четвертом интервале уравнение превратится в тождество,
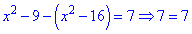
это означает, что все точки из интервала являются решениями .
Таким образом , решением будут два промежутка
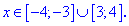
Для наглядности графики модуля вместе с правой частью изображены графически
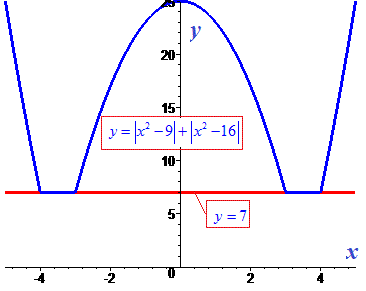
Пример 7. Найти решение уравнения
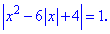
Решение:Имеем квадратное уравнение под модулем, кроме того переменная в нем также содержится под модулем. Такого рода задачи вызывают немало трудностей при решении у начинающих, но для профи такие примеры не сложные . В первую очередь избавляемся модуля у переменной.
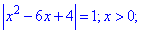
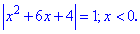
Такого рода примеры приводят к большому количеству областей, поэтому можно решать применяя разбиение на промежутки, а можно решать самые уравнения, а после того проверять решения подстановкой.
Оба уравнения при раскрытии модулей дают следующие
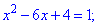
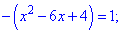
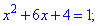
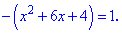
Находим корни первого уравнения
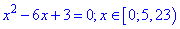
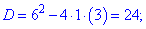
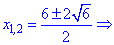
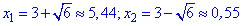
Решаем второе квадратное уравнение
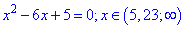
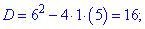
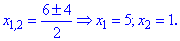
С третьего уравнения
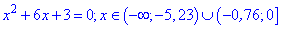
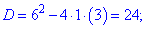
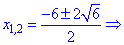
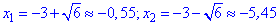
получаем два решения.
Из последнего - 4 уравнения
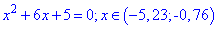
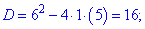
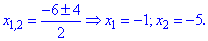
получаем два корня . Всего получили 8 решений уравнения с модулями. Проверка подстановкой показывает что они все подходят. Также для подтверждения ниже приведен график фигурирующих модулей.
Все рассмотренные примеры достаточно просто решаются в математическом пакете Maple. Код программы с решениями приведен ниже
> restart;
> Q1:=abs(5*x-10)=11;
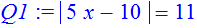
> solve(Q1,x);
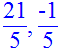
> Q2:=abs(1-5*x)=abs(2-x);
> solve(Q2,x);
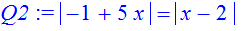
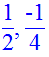
> Q3:=abs(x+3)-abs(x-5)=3*x+4;
> solve(Q3,x);
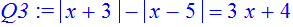
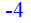
> Q4:=x^2-5*abs(x)-24=0;
> solve(Q4,x);
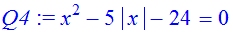
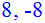
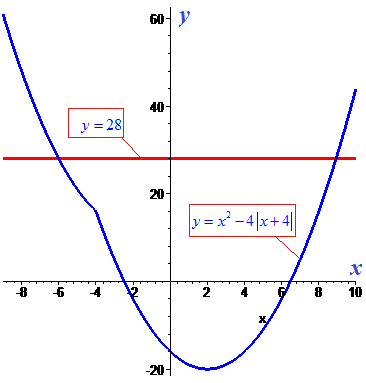
> Q5:=x^2-4*abs(x+4)=28;
> solve(Q5,x);
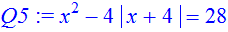
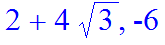
> Q6:=abs(x^2-9)+abs(x^2-16)=7;
> solve(Q6,x);
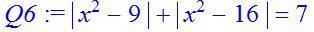
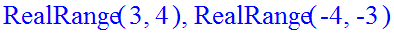
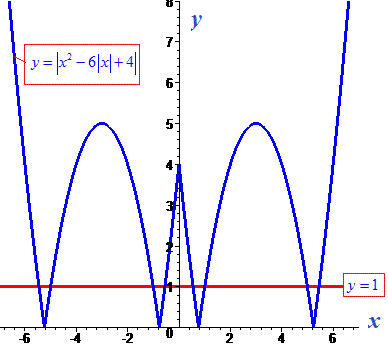
> Q7:=abs(x^2-6*abs(x)+4)=1;
> solve(Q7,x);
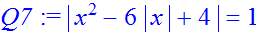
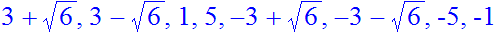
Уравнение с модулями требуют большого внимания при решении. Самая меньшая невнимательность или ошибка со знаком может привести к лишним решениям или их нехватке. При вычислениях можете выполнять проверку методом подстановки или с помощью Maple или других известных Вам программ.
Похожие материалы:


