Продовжуємо розбір циклу статей на застосування властивостей показникових та логарифмічних функцій для спрощення виразів, що їх містять. Сьогодні будемо знайомити Вас з черговою добіркою розв'язків прикладів із ЗНО підготовки. Загалом на сайті розв'язаний цілий збірник, тож підготовка онлайн до тестування та вступу у ВУЗи піде на користь усім. В першу чергу абітурієнтам, далі учням 10-11 класів, які вивчають цей матеріал на уроках, ну і звичайно батькам, адже з такими поясненнями репетитори не потрібні (а це в наш час чималі грошенята).
Головне дорогі читачі – більше розв'язуйте однотипних прикладів самостійно.
Приклад 6.22 Обчислити: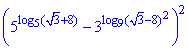 
А | Б | В | Г | Д |
64 | 12 | 8 | 2 | 65-16√3 |
Розв'язування: Застосуємо основну логарифмічну тотожність 
для обчислення значення виразу
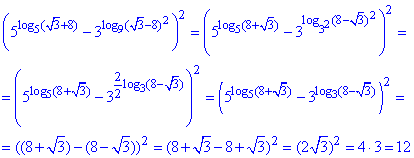
Відповідь: 12 – Б.
Приклад 6.23 Спростити логарифм:
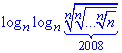
А | Б | В | Г | Д |
2008 | -2008 | 1004 | -1004 | 1 |
Розв'язування: Важко уявити собі 2008 вкладених коренів, але завдяки представленню їх в показниковій формі, легко отримати компактний його запис:
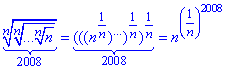
Далі підставляємо отриманий вираз у вложені логарифми та виносимо показники з під логарифмів
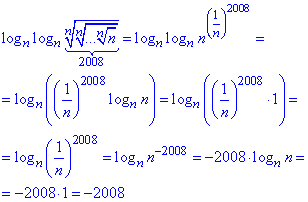
Таких завдань багато, і з роками вчителі змінюють тільки рік, який настає 2020, 21, ... на зміну попередньому.
Відповідь: -2008 – Б.
Приклад 6.24 Установити відповідність між виразами (1–4) та виразами, які їм тотожно дорівнюють (А–Д).
1. 2lg5+lg4 | А. 5 |
Розв'язування: На ЗНО тестах одне таке завдання дозволяє перевірити чи Ви знаєте властивості логарифма? та скільки їх використовуєте?
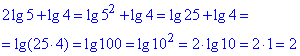
На перше завдання тестів відповідь 2 - Г.
В другому завданні маємо готову формулу переходу від однієї основи логарифма до іншої, але її слід пам'ятати, щоб не поміняти навпаки основу з підлогарифмічим числом.
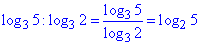
Третє завдання розписуємо за формулою різниціі логарифмів з однаковою основою
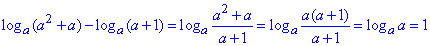3 - В.
Застосовуємо основу логарифмічну тотожність, попередньо винісши показники основи та числа з під логарифма:
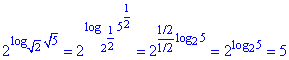4 - А.
Приклад 6.25 Установити відповідність між виразами (1–4) та їхніми значеннями (А–Д).
Розв'язування: Останні завдання ЗНО тестів мають по 4 завдання + оцінюються більшою клькістю балів.
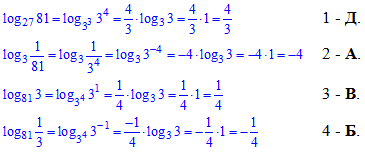
Погляньте на обчислення, вони не складні і під силу учням, які не лінуються працювати самостійно.
Приклад 6.26 Установити відповідність між виразами (1–4) та їхніми значеннями (А–Д).
Розв'язування: Завдання на знання правил винесення степені з основи логарифма та виразу під логарифмом.
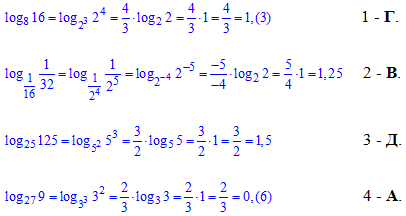
Просте правило, яке дозволяє швидко знайти відповіді до тестів:
показник від числа у логарифмі виносимо множником перед логарифм;
logabk=k•logab
степінь основи логарифма при винесенні з під логарифма є оберненим множником перед логарифмом.
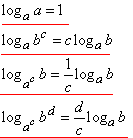
Приклад 6.27 Установити відповідність між виразами (1–4) та їхніми значеннями (А–Д).
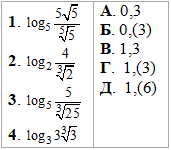
Розв'язування: Завдання хоч і містить логарифми, але в плані обчислень вимагає добрих знань властивостей показникових функцій. Саме від того, як Ви вмієте звести корінь n-го степеня до показникової форми та знаєте правила додавання і множення показників залежить правильність отриманих результатів.
Перегляньте завдання, можливо одне з них чекає на ЗНО тестах чи контрольній роботі з математики.
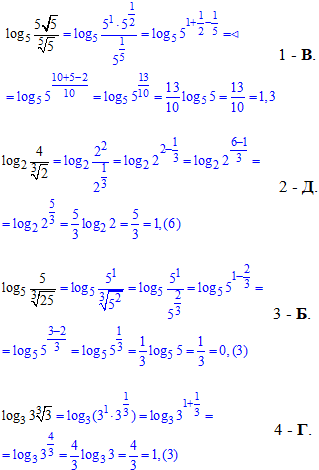
Операції додавання та віднімання дробових степенів не важкі, тому розгляньте основні моменти, які у формулах підкреслені та вчіться розписувати вирази самостійно. Попереду Вас чекають набагато складніші завдання на спрощення логарифмічних та показникових виразів.
Приклад 6.28 Установити відповідність між виразами (1–4) та їхніми значеннями (А–Д).
Розв'язування: Тестові завдання на знання формул логарифмічного множення та додавання обчислюють за наведеною схемою:
Усі 4 приклади зводимо до дробу, де вчисельнику і знаменнику маємо логарифми основ – вони рівні одиниці. Множники при логарифмах і дають значення виразу після спрощень.
Приклад 6.29 Установити відповідність між виразами (1– 4) та їхніми значеннями (А–Д).
Розв'язування: Усі чотири завдання вирішують за наступною схемою:
в показнику числа маємо логарифми, тому при розв'язуванні тестів слід скористатися основною логарифімчною тотожністю
Перед тим як це робити, корінь квадратний з √3 виразимо в показниковій формі 3^(1/2), 4 в першому прикладі зведемо до основи логарифма 2, в другому та четвертому завданні розпишемо степені за правилами додавання та віднімання.
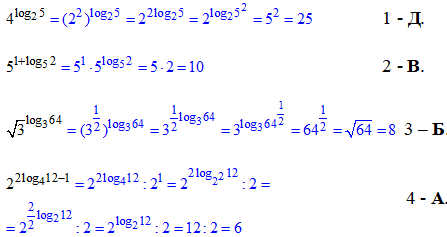
Сподіваємося, Ви багато повчального винесли з цієї статті, але це ще не все що ми підготували, на цьому розбір завдань не завершено. Усього їх 48, а ця стаття закінчується 29-им прикладом із ЗНО тестів. Складніші приклади та схеми їх обчислень чекають Вас попереду.
