Продовжуємо розбір відповідей до ірраціональних рівнянь, які підібрані зі збірника для ЗНО підготовки. Кожне з рівнянь вносить маленький вклад у Ваше навчання, тому уважно їх розглядайте та використовуйте в самоосвіті.
Приклад 12.14 Скільки цілих коренів має рівняння 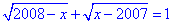 ?
?
А | Б | В | Г | Д |
Жодного | один | два | три | чотири |
Обчислення: Загалом ірраціональні рівняння можуть мати зліченну, незліченну множину коренів або порожню.
Зараз розберемося від чого це залежить.
В першу чергу від області визначення, а вона напряму визначається з обмеження на значення підкореневих функцій:
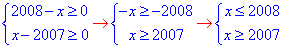
звідси x∈[2007;2008].
Розв'язком ОДЗ є проміжок, який містить лише два цілих числа, а саме 2007 і 2008.
Підставимо їх у задане рівняння і перевіримо, чи є ці числа його коренями:
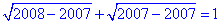 звідси 1=1;
звідси 1=1;
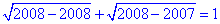 звідси 1=1;
звідси 1=1;
Робимо висновок, що задане рівняння має два цілих корені, а саме x1=2007 і x2=2008.
Відповідь: два – В.
Приклад 12.15 Скільки ірраціональних коренів має рівняння 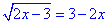 ?
?
А | Б | В | Г | Д |
Жодного | один | два | три | чотири |
Обчислення: Під ірраціональними тут мають на увазі, що корені рівняння є коренями чисел.
Почнемо з розгляду області визначення.
Коренева функція повинна бути невід'ємною, при цьому права сторона також повинна приймати значення більші або рівні нулю.
Не забувайте про останню умову в прикладах.
Таким чином дістаємо дві нерівності для ОДЗ:
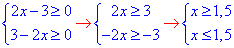
звідси x=1,5.
Розв'язком ОДЗ є лише одне число, а саме 1,5, яке не є ірраціональним, тому задане рівняння не має ірраціональних коренів
(Підстановкою можете переконатися, що коренем рівняння є лише одне число, а саме x=1,5).
Відповідь: Жодного – А.
Приклад 12.16 Скільки коренів має рівняння 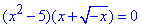 ?
?
А | Б | В | Г | Д |
Жодного | один | два | три | чотири |
Обчислення: Розпочинаємо обчислення з ОДЗ:
-x≥0, x≤0, звідси x∈(-∞;0].
Розв'яжемо ірраціональне рівняння:
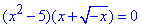
x2-5=0,
x2=5,
звідси x1= √5 (не належить ОДЗ) і x2=-√5;
x+ √-x=0,
√-x=-x,
(√-x)2=(-x)2,
-x=x2,
x2+x=0,
x(x+1)=0,
звідси x3=0 і x4=-1.
В підсумку отримали, що задане рівняння має три корені, а саме x=-√5, x=0 і x=-1.
Відповідь: три – Г.
Приклад 12.17 Розв'язати рівняння 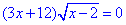 .
.
А | Б | В | Г | Д |
-4 | -4; 2 | 2 | -2; 4 | -2 |
Обчислення: Випишемо нерівність, що накладає множник з коренем квадратним:
x-2≥0,
звідси x≥2, або x∈[2;+∞).
Кожен з множників рівняння 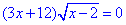 прирівняємо до нуля та знайдемо розв'язки.
прирівняємо до нуля та знайдемо розв'язки.
1. 3x+12=0,
3x=-12,
звідси x1=-4 (не належить ОДЗ);
2. 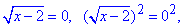
x-2=0, звідси x2=2.
Отже, задане рівняння має один корінь, а саме x=2.
Не забувайте перевіряти чи належать корені ОДЗ (або виконуйте підстановку).
Без перевірки багато б з Вас помилково отримали два корені, які відповідають варіанту Б ЗНО тестів, що є неправильно.
Відповідь: 2 – В.
Приклад 12.18 Знайти суму коренів рівняння 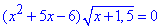 .
.
А | Б | В | Г | Д |
-6,5 | 3,5 | -5 | -2,5 | -0,5 |
Обчислення: Випишемо обмеження на область визначення.
ОДЗ: x+1,5≥0, звідси x≥-1,5, тобто x∈[-1,5;+∞).
Далі кожен з множників у рівнянні 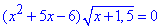 прирівнюємо до нуля та знаходимо корені.
прирівнюємо до нуля та знаходимо корені.
1. Квадратне рівняння x2+5x-6=0
дає два розв'язки x1=-6 (не належить ОДЗ) і x2=1.
2. 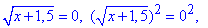
x+1,5=0, звідси x3=-1,5.
В підсумку, задане ірраціональне рівняння має два корені, а саме x2=1 і x3=-1,5.
Знайдемо їх суму:
x2+x3=1+(-1,5)=-0,5
Відповідь: -0,5 – Д.
Приклад 12.19 Скільки коренів має рівняння 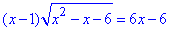 ?
?
А | Б | В | Г | Д |
Жодного | один | два | три | чотири |
Обчислення: Під коренем маємо квадратний тричлен, для з'ясування де він невід'ємний доведеться вирішити наступну нерівність:
x^2-x-6≥0,
(x-3)(x+2)≥0,
Побудуємо множину розв'язків ОДЗ на числовій осі
 ОДЗ: x∈(-∞;-2] ∪[-3;+∞).
ОДЗ: x∈(-∞;-2] ∪[-3;+∞).
Наведемо методику розв'язування таких рівнянь:
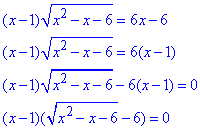
В правій частині маємо нуль, тому кожен з множників прирівнюємо до нуля і розв'язуємо.
1. x-1=0, звідси x1=1 (не належить ОДЗ);
2. Ірраціональне рівняння зводимо до квадратного
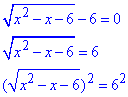
x2-x-6=36
x2-x-x-42=0,
звідси x2=-6 і x3=7.
Отже, задане рівняння має два корені x=-6 і x=7.
Відповідь: два – В.
Приклад 12.20 Розв'язати рівняння 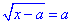
 Обчислення: Виписуємо ОДЗ:
Обчислення: Виписуємо ОДЗ:
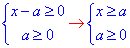
Не забувайте, що в таких рівняннях права сторона теж повинна бути невід'ємна (якщо корінь квадратний невід'ємний).
Таким чином дістанемо:
якщо a<0, тоді x∈∅;
якщо a≥0, тоді x≥a.
Знайдемо розв'язок рівняння:
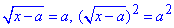
x-a=a2, звідси x=a2+a.
Отже, задане рівняння має корінь, а саме x=a2+a, якщо a≥0.
Відповідь: Г.
Приклад 12.21 Розв'язати рівняння 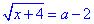
 Обчислення: З'ясовуємо область визначення рівняння з нерівностей:
Обчислення: З'ясовуємо область визначення рівняння з нерівностей:
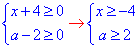
отже:
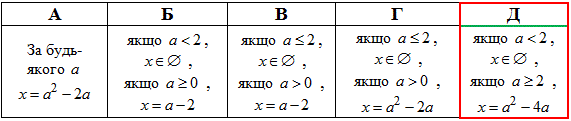
якщо a<2, то x∈∅;
якщо a≥2, то x≥-4.
Розв'яжемо рівняння:
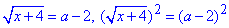
x+4=a2-4a+4,
звідси x=a2-4a.
Задане рівняння має корінь x=a2-4a, якщо a≥2.
Відповідь: Д.
Приклад 12.22 Знайти всі значення параметра a, за яких рівняння 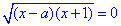 та
та 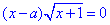 рівносильні.
рівносильні.
А | Б | В | Г | Д |
a≤-1 | a=-1 | a>-1 | a≥-1 | a<-1 |
Обчислення: Рівняння називаються рівносильними, якщо множини їх розв'язків співпадають.
Забігаючи наперед, поділимося методикою обчислень:
розв'язуємо обидва рівняння незалежно одне від одного, а далі співставляємо за яких значень параметра розв'язки обох рівнянь співпадають.
1.Обчислимо перше з рівнянь
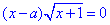
ОДЗ: x+1≥0, звідси x≥-1.
Тоді x+1=0, звідси x1=-1 і x-a=0, звідси x2=a.
2.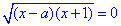
ОДЗ: (x-a)(x+1) ≥0.
Якщо a≥-1, то отримаємо наступні знаки на інтервалах
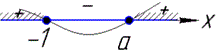
звідси x∈(-∞;-1] ∪[a;+∞).
Якщо a ≤-1, то знаки на числовій осі змінюватимуться за правилом

звідси x∈(-∞;a] ∪[-1;+∞).
Але, якщо a<-1, то рівняння 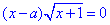 матиме єдиний розв'язок x=-1 (тут x=a не задовольняє ОДЗ, оскльки a+1<0), а рівняння
матиме єдиний розв'язок x=-1 (тут x=a не задовольняє ОДЗ, оскльки a+1<0), а рівняння 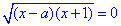 матиме два розв'язки x1=-1, x2=a і тоді задані рівняння не будуть рівносильними.
матиме два розв'язки x1=-1, x2=a і тоді задані рівняння не будуть рівносильними.
При a≥-1 обидва рівняння матимуть два розв'язки x1=-1, x2=a (a+1≥0, тому задовольняє ОДЗ), тобто будуть рівносильними.
Відповідь: a≥-1 – Г.
Якщо Ви думаєте, що це все що в нас є з ірраціональних рівнянь то помиляєтеся.
Всього в цьому курсі підготовки до ЗНО міститься 48 прикладів, від найпростіших до складних.
Це ще навіть не половина прикладів з готовими відповідями з якими Ви можете ознайомитися і використати у навчанні.
Чекаємо Вашої активної участі в розвитку сайту та доповненні розділів новими матеріалами.


