Розкриття показникових нерівностей

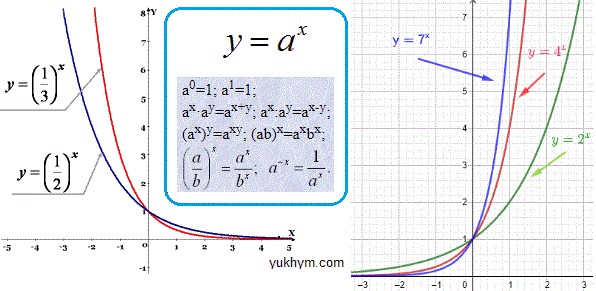
Щоб навчитися методик розкриття показникових нерівностей, потрібні добрі знання властивостей функцій. З приведених далі графіків Ви можете бачити, що показникова функція є монотонною постійно зростаючою, якщо основа більша одиниці (a>1)
або монотонно спадною, якщо основа менша одиниці (0<a<1).
Для розкриття нерівностей Ви повинні вивчити та знати правила додавання та множення степенів, які виділені в формулах.

Розглянемо правила рівносильних перетворень показникових нерівностей.

Основа більша одиниці a>1

Показникова нерівність a^f(x)<a^g(x) є рівносильною нерівності для степенів f(x)<g(x), якщо a>1.
a^f(x)<a^g(x)⇔f(x)<g(x).
Симетрично, для знаку більше ">":
a^f(x)>a^g(x)⇔f(x)>g(x).
Правила розкриття нестрогих показникових нерівностей аналогічні:
a^f(x)≤a^g(x)⇔f(x)≤g(x);
a^f(x)≥a^g(x)⇔f(x)≥g(x).

Основа менша одиниці 0<a<1

Нерівність a^f(x)>a^g(x) є рівносильною нерівності для степенів, взятої з протилежним знаком f(x)<g(x), якщо 0<a<1.
a^f(x)<a^g(x)⇔f(x)>g(x);
a^f(x)≤a^g(x)⇔f(x)≥g(x);
a^f(x)≥a^g(x)⇔f(x)≤g(x).

Розглянемо приклади на кожен з випадків.

Основа більша за одиницю

Приклад 15.12 Розв'язати нерівність 2^x+1+2^x<24.

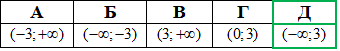
Розв'язування: Вирази, що містять змінну групуємо, виносимо найменший спільний множник 2^x, а все що залишиться в дужках переносимо в праву сторону.
Далі зводимо обидві сторони до спільної основи

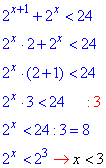
та методом інтервалів розв'язуємо

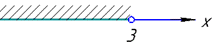
Нерівність строга, тому точку x=3 не включаємо.
В підсумку, маємо x∈(-∞;3).
Відповідь:(-∞;3) – Д.

Приклад 15.19 Розв'язати нерівність

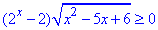
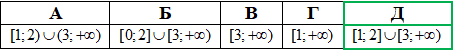
Розв'язування: Нерівність рівносильна системі:

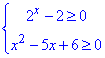
Розв'яжемо рівняння

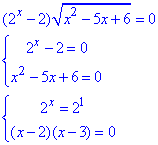
тоді його корені x₁=1, x₂=2 і x₃=3.
Розглянемо нерівності

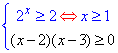
Метод інтервалів визначаємо множину її розв'язків

Звідси слідує, що показникова нерівність виконується на інтервалах x∈[1;2]∪[3;+∞).
Відповідь:[1;2]∪[3;+∞) – Д.

Приклад 15.25 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).

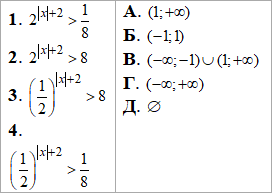
Розв'язування: Усі чотири нерівності в степені мають модулі, тому при їх розкритті будемо мати або дві нерівності, які обмежують інтервал коренів або порожню множину розв'язків. Детальні пояснення перегляньте з наступних таблиць:


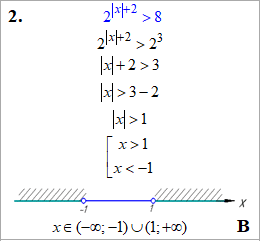
Останні два варіанти на основу (1/2<1) меншу одиниці, тому уважно перегляньте, що змінилося при розкритті нерівностей та порівнянні степенів при однакових основах.

Основа менша одиниці

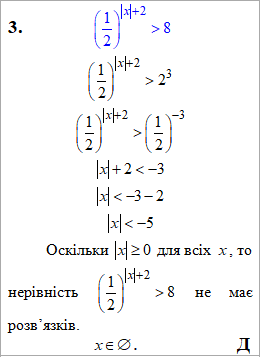
З формул можна зауважити, що при опусканні основ та порівнянні степенів знак нерівності змінили на протилежний. Таке правило зумовлене тим, що маємо випадок коли основа належить інтервалу 0<a<1. Запам'ятайте це правило, та не забувайте при обчисленнях.

Приклад 15.16 Указати найменший розв'язок нерівності (2/5)^x+2≤(5/2)².

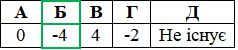
Розв'язування:Зводимо нерівність до однієї основи 2/5<1, після чого розкриваємо її та при розкритт змінюємо знак на протилежний

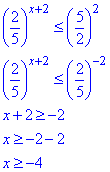
звідси x∈[-4;+∞).
Наносимо множину розв'язків на числову вісь

Нерівність нестрога, тому x=-4 – найменший її розв’язок.
Відповідь:-4 – Б.

Наступні приклади ми рекомендуємо переглядати учням 10-11 класів при підготовці до участі в олімпіадах.

Приклад 15.20 Розв’язати нерівність 2^x²>sin(x).

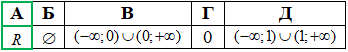
Розв'язування: Вираз 2^x²≥1 завжди не менший одиниці, оскільки квадрат x²≥0 для будь-якого x.
Значення синус функції лежать в інтервалі -1≤sin(x)≤1.
При x=0 отримаємо 2⁰>sin(0), тобто 1>0.
При всіх інших x маємо 2^x²>sin(x), оскільки 2^x² буде більше за 1, а значення sin(x) – менше за 1.
Тому розв’язком заданої нерівності 2^x²>sin(x) є множина дійсних чисел, тобто x∈R.
Відповідь:R – А.

Приклад 15.22 Установити відповідність між нерівностями (1–4) та множинами їх розв’язків (А–Д).

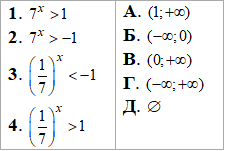
Розв'язування: Маємо чотири показникові нерівності, права сторона чких рівна або одиниці або мінус одиниці. З властивостей показникових функцій знаємо, що якщо основа більша за одиницю то показникова функція всюди додатна. Звідси, можемо встановити множину розв'язків 2-го та 3-го варіантів тесту. Повні пояснення наведені далі:

Показникові нерівності з параметром

Приклад 15.21 За якого значення параметра a нерівність a²-2•4^x+1-a•2^x+1>0 не має розв'язків?

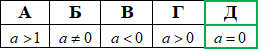
Розв'язування: Щоб розкрити показникову нерівність, перетворимо її до квадратної

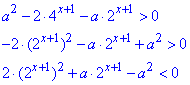
Вводимо заміну змінних: 2^x+1=t, де t>0.
Обчислимо дискримінант рівняння та, оскільки він містить параметр, проведемо аналіз його можливих значень

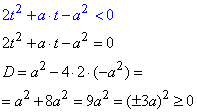
1) Нехай дискримінант рівний нулю D=0.
Тоді параметр рівний нулю a=0, звідси

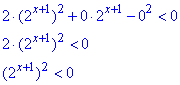
Очевидно, що задана нерівність не матиме розв'язків, оскільки квадрат будь-якого числа більший або рівний нулю, а вираз (2^x+1)²>0 додатний для будь-яких x.

2) Нехай дискримінант додатний D>0.
Тоді маємо два корені

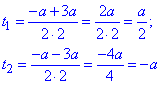
при яких розв'язуємо показникові рівняння логарифмуванням

Звідси слідує, що нерівність a²-2•4^x+1-a•2^x+1>0 не має розв'язків, якщо параметр a=0.
Відповідь:a=0 – Д.

Нерівності з параметром вимагають більше уваги ніж звичайні, оскільки розширюють можливі варіанти розв'язків і кожну умову доводиться розбирати окремо.
На цьому урок завершено, більше розв'язків ЗНО тестів на показникові нерівності Ви можете переглянути з наступних двох статей.