"Розв'язати рівняння з модулями" або "Знайти усі розв'язки рівняння з модулями" – одні з найпопулярніших завдань в шкільному курсі математики, та на першому курсі у ВУЗах при вивченні модулів. Завдання легко зводяться до звичайних рівнянь при знанні правил, а вони досить прості. При розкритті модуля потрібно знайти точки в яких підмодульна функція приймає нульове значення. Дійсну вісь розбити знайденими точками на інтервали та встановити знаки функції на кожному з них. Дальше розкривають модулі за правилом:
Якщо підмодульна функція додатна, то модулі розкривають без змін. Якщо від'ємна, то розкриваючи модуль функцію беруть зі знаком мінус.
Все це напряму випливає з означення модуля числа:
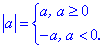
Після обчислень перевіряють, чи належить розв'язок розглядуваному інтервалі чи ні. В такий спосіб відсівають зайві результати.
Для наочності перейдемо до обчислень.
Приклад 1. Знайти розв'язок рівняння
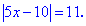
Розв'язання: Задане завдання є найпростішим типом рівнянь з модулями. В першу чергу рівняння містить модуль один раз та змінна входить лінійно.
Знаходимо точку, в якій вираз під знаком модуля перетворюється в нуль
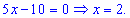
Справа від цієї точки вираз під модулем приймає додатне значення, зліва – від'ємне.
Розкриваючи модуль, отримаємо два рівняння з умовами на невідому
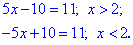
Знаходимо розв'язки
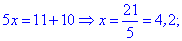
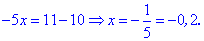
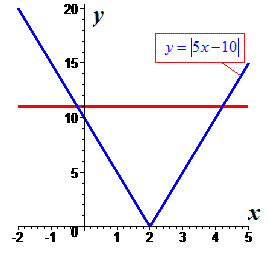
Такого типу рівняння з модулем можна розв'язати графічним методом. В результаті отримаємо наступний вигляд функцій
Приклад 2. Знайти корені рівняння
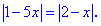
Розв'язання: Розв'язуємо за схемою попереднього прикладу.
Знаходимо точки в яких модулі перетворюються в нуль.
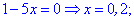
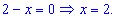
Обидві точки розділяють дійсну вісь на інтервали.
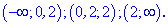
Позначаємо знаки підмодульних функцій на знайдених інтервалах. Знаки встановлюємо простою підстановкою точок з інтервалу
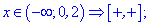
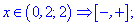
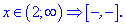
Для зручності можете позначати інтервали графічно, декому це дуже допомагає, однак можна обійтися лише наведеними вище записами.
Розкриваємо модулі, враховуючи знаки та знаходимо розв'язки.
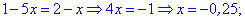
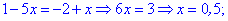
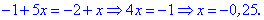
Останній розв'язок не має змісту, оскільки не належить проміжку на якому його знаходимо. Таким чином рівняння задовільняють значення
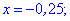
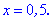
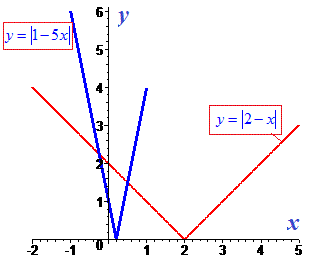
Графік модуль-функцій наведено нижче, точки їх перетину і є розв'язком.
Приклад 3. Знайти розв'язок рівняння
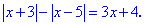
Розв'язання: Знаходимо точки, які розбивають вісь на області знакосталості
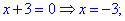
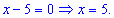
Визначаємо знаки підмодульних функцій на цих областях
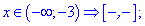
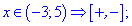
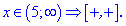
Розкриваємо модулі та обчислюємо
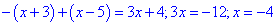
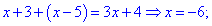
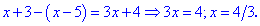
Другий і третій розв'язки не належать проміжку, отже рівнянню відповідає лише x=-4.
Графіки модулів зображено графічно
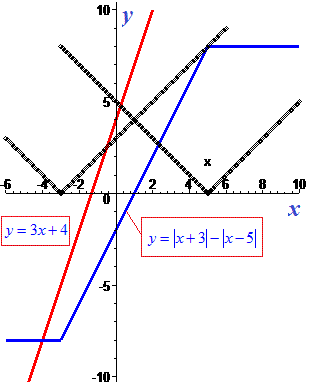
Приклад 4. Знайти розв'язок рівняння
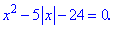
Розв'язання: Маємо квадратний тричлен, який зводиться до розв'язування двох рівнянь
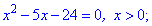
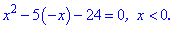
Розв'язуємо кожне з квадратних рівнянь. Дискримінант у них буде однаковий
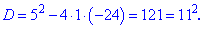
Знаходимо корені першого рівняння
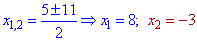
та другого
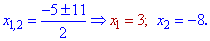
Позначені корені рівняння не належать області, на якій шукали розв'язок. Остаточно отримали два корені рівняння з модулем
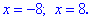
На графіку модуль-функції розв'язок є перетином з віссю Ox
Приклад 5. Визначити корені рівняння
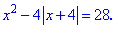
Розв'язання: Точка x=-4 ділить область на інтервали
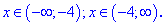
На першому інтервалі отримаємо квадратне рівняння
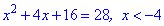
на другому відповідно наступне
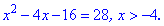
Обчислюємо дискримінант першого
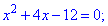
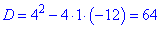
та корені
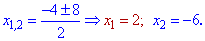
Друге рівняння буде мати розв'язки
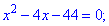
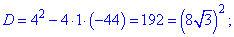
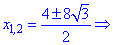
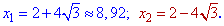
Два корені відпадають, а два є розв'язками
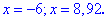
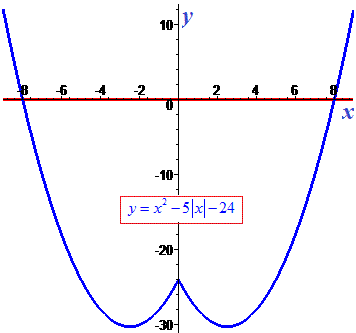
Графік функції з модулем разом із точками перетину ілюструє наступний рисунок
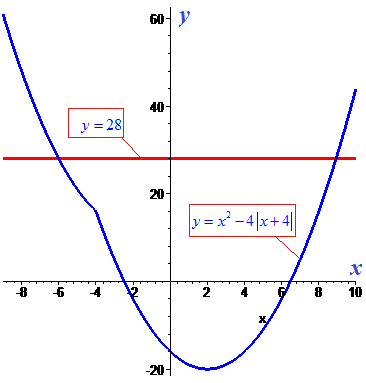
Приклад 6. Знайти усі розв'язки рівняння з модулями
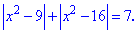
Розв'язання: Схема розв'язування попередня. Знаходимо нулі
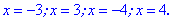
Вони ділять область на п'ять інтервалів, в яких знаходимо знаки функцій
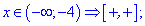
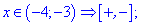
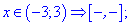
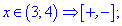
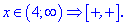
Розкриємо модулі для першої та п'ятої областей
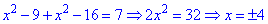
Дані точки належать краю області, однак при підстановці рівняння перетворюється в тотожність.
Другий інтервал
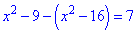
перетворюється в тотожність, отже всі точки інтервалу включно з краями є розв'язками.
Третій інтервал
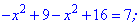
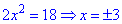
дає два корені, які задовільняють вихідне рівняння з модулями.
На четвертому інтервалі рівняння перетвориться у тотожність,
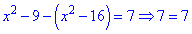
це означає, що всі точки з інтервалу є розв'язками.
Таким чином, розв'язком будуть два проміжки
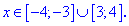
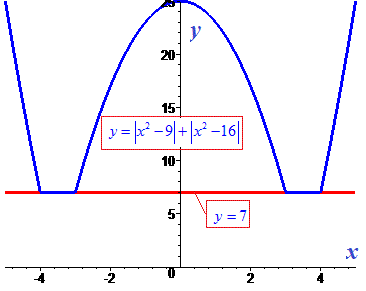
Для наочності графік модуля разом із правою частиною зображено графічно
Приклад 7. Знайти корені рівняння модуль в модулі
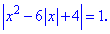
Розв'язання: Маємо квадратне рівняння під модулем, крім того змінна у ньому також міститься під модулем. Такого роду завдання викликають чимало труднощів при розв'язуванні у початківців, однак для "профі" такі приклади не складні. В першу чергу позбуваємося модуля біля змінної.
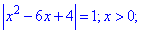
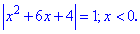
Такого роду приклади приводять до великої кількості областей, тому можна розв'язувати застосовуючи розбиття на проміжки, а можна розв'язувати самі рівняння, а після того перевіряти підстановкою.
Обидва рівняння при розкритті модулів дають наступні
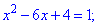
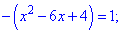
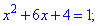
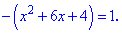
Знаходимо корені першого рівняння
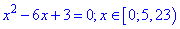
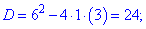
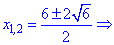
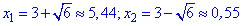
Розв'язуємо друге квадратне рівняння
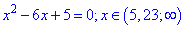
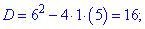
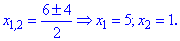
З третього рівняння через дискримінант
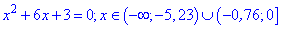
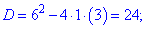
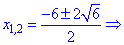
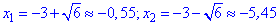
отримуємо два розв'язки.
З останнього – четвертого рівняння
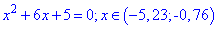
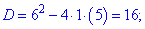
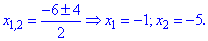
отримуємо два корені. Загалом отримали 8 розв'язків рівняння з модулями. Перевірка підстановкою показує, що вони всі підходять. Також для підтвердження нижче наведено графік модуль функції
Всі розглянуті приклади досить просто вирішуються в математичному пакеті Maple. Код програми з отриманими розв'язками наведено нижче
> restart;
> Q1:=abs(5*x-10)=11;
![]()
> solve(Q1,x);
![]()
> Q2:=abs(1-5*x)=abs(2-x);
> solve(Q2,x);
![]()
![]()
> Q3:=abs(x+3)-abs(x-5)=3*x+4;
> solve(Q3,x);
![]()
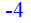
> Q4:=x^2-5*abs(x)-24=0;
> solve(Q4,x);
![]()
![]()
> Q5:=x^2-4*abs(x+4)=28;
> solve(Q5,x);
![]()
![]()
> Q6:=abs(x^2-9)+abs(x^2-16)=7;
> solve(Q6,x);
![]()
![]()
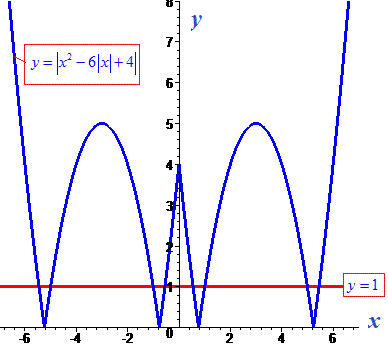
> Q7:=abs(x^2-6*abs(x)+4)=1;
> solve(Q7,x);
![]()
![]()
Рівняння з модулями потребують великої уваги при розв'язанні. Сама менша неуважність або помилка зі знаком може привести до зайвих розв'язків або їх недостачі. При обчисленнях можете виконувати перевірку методом підстановки або за допомогою Maple чи інших відомих Вам програм.
Переглянути схожі матеріали:


