Задачи на простые проценты встречаются в школьном курсе алгебры, экономике, банковской сфере и т.д. Без понимания их содержания и знания формул решить задачи часто бывает сложно. Ниже на распространенных примерах будут даны основные задачи и формулы для их решения.
Процентом ( процентом ) от числа А называется одна сотая часть этого числа. Слово «процент» произошло от латинского pro centо, что значит «с сотни ». Обозначение процентов «%» происходит от искажения письменного сto.
Например: 10% = 0,1; 10 часть числа А.
В случае кредитов и депозитов используют формулы для вычисления простых процентов на период в годах, месяцах и днях. Задачи не требуют сложных вычислений и понравятся как школьникам, так и тем, кто первый раз знакомится с процентами. На практике проценты используют в банковской сфере, химии, медицине, хозяйстве.
Другая часть задач касается нахождения содержания чего-то по известным процентами, или наоборот - за содержанием найти процентное соотношение.
Оба типа задач будут рассмотрены ниже.
Простой процент на период в годах
Формула простого процента на период в годах
P[i]=P*(1+n/100*r)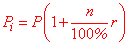 
где P[i] – увеличение величины P через r лет, если ставка составляет n процентов. Величиной P могут выступать депозиты, кредиты, материалы.
Задача 1. Вкладчик разместил сумму размером 2400 рублей в банк. Определите, какую сумму получит вкладчик через 3 года, если процентная ставка составляет 19 % в год.
Решение: Данные задачи подставляем в формулу простых процентов
P[3]=2400*(1+19/100*3)=3768 (рублей.)
Таким образом за 3 года вкладчик получит 3768 рублей.
Обратная задача на проценты
Обратной задачей на проценты называют такую, в которой за неизвестные выступают количество лет или процентная ставка.
Задача 2. Вкладчик взял в кредит 3000 рублей и должен вернуть через пять лет. Найти процентную ставку кредита, если известно, что нужно отдать банку 8100 грн.
Решение: Выведем формулу для этой задачи.
P[i]=P*(1+n/100*r);
P[i]/P=1+n/100*r;
n= (P[i]/P-1)/r*100.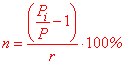
Выполняем вычисления по выведенной формуле
n= (8100/3000-1)/5*100=1,7/5*100=34 (%).
Следовательно, процентная ставка кредита составляет 34 %.
Если в обратной задачи на проценты нужно найти количество лет, то нужная формула на основе предыдущих выкладок будет выглядеть
r= (P[i]/P-1)/n*100
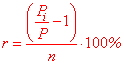
Расчет простых процентов за период в несколько месяцев
Формула простых процентов в этом случае будет иметь вид
P[i]=P*(1+n/100*m/12)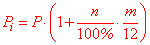
здесь обозначено m – количество месяцев (month).
Задача 3. Вкладчик разместил сумму размером 1600 рублей в банк на один год, однако ему пришлось забрать деньги через семь месяцев. Процентная ставка при досрочном снятии депозита составляет 9 % в год. Найти сумму, которую получит вкладчик.
Решение: Применяем формулу для вычислений
P[3]=1600*(1+9/100*7/12)=1684 (рублей.)
За 7 месяцев вкладчик получит 1684 рублей.
Из приведенной формулы достаточно просто получить все необходимые величины для обратной задачи.
Количество месяцев определяют по формуле
m= (P[i]/P-1)/n*100*12
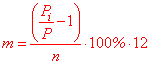
а процентную ставку находят из зависимости
n= (P[i]/P-1)/m*100*12
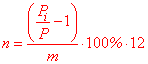
Расчет простых процентов за период в днях
Данный тип задач применяют при имитации кратковременных кредитов или депозитов. Формула начислений имеет вид
P[i]=P*(1+n/100*d/365)
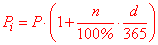
здесь d – количество дней.
Задача 4. Заемщик получил кредит на сумму 20000 рублей под 32% годовых. Через 240 дней кредит был полностью погашен. Рассчитайте, какую сумму заемщик отдал банку? Насколько отличается эта сумма от одолженной?
Решение: Применяем формулу простых процентов для вычислений
P[i]=20000*(1+32/100*240/365)=24208,22 (рублей)
24208,22-20000=4208,22 (рублей)
Получили, что за этот период насчитана сума 4208,22 рублей.
Простые проценты в математике
Задача 5. В класс закупили 3 энергосберегающие окна, которые на 20 % дороже обычных. Сколько потратили денег, если за обычные окна нужно заплатить 1400 гривен.
Решение: Найдем цену энергосберегающего окна
P[в]=1400*(1+20/100)=1680 (грн.)
За три окна заплатили
1680*3=5040 (грн).
Задача 6. В бочке объемом 200 литров перевозили масло . На станции отлили 60 литров. Сколько процентов от обьема осталось?
Решение: Задача состоит в нахождении количества в процентах масла от общего объема бочки.
200-60=140 (л);
140/200*100%=70 %
Осталось 70% объема бочки.
Задача 7. При несвоевременной уплате долгов насчитывают 2% пени за каждый просроченный день. Какую сумму нужно заплатить через 12 дней после срока погашения 500 рублей долга?
Решение: По формуле простых процентов находим
P[i]=500*(1+2/100*12)=620 (рублей)
Нужно заплатить 620 рублей.
Рассмотрим задачи из учебника для 9 класса авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир « Аглгебра ». (Номер в скобках)
Задача 8. (542) К сплаву массой 600 г, содержащему 12 % серебра, добавили 60 г серебра. Какое содержание серебра в новом сплаве?
Решение: Определяем сколько грамм серебра в первом сплаве
P[i]=600*12/100=72 (г)
К найденному значению добавляем 60 грамм серебра
P1=72+60=132 (г)
При определении процентного содержания серебра не следует забывать, что вес нового сплава вырос на массу серебра, которую добавили.
Если би Вы вычисляли следующим образом
132/600*100%=22%
то получили - неправильный результат .
ЗАПОМНИТЕ: в подобных задачах сначала находят меру ( вес, объем, длину) нового объекта, а затем находят содержание.
В заданной задачи новый сплав получит массу
P2=600+60=660 (г)
а процентное содержание серебра
P1/P2*100%=132/660*100%=20 %
будет следующим - 20%.
Задача 9. (543) В саду росли яблони и вишни, причем яблони составляли 42% всех деревьев. Вишен было на 48 деревьев больше, чем яблонь. Сколько деревьев росло в саду?
Решение: К правильному ответу можно идти несколькими способами. Рассмотрим следующий из них.
Пусть яблони составляют 42% всех деревьев, тогда вишни
100-42=58%.
Вишен на 48 больше нежели яблонь.
Разница между ними в процентах составляет
58-42=16%
а в количестве - 48 деревьев.
Задача состоит в нахождении количества деревьев, поэтому складываем отношения
16% – 48 деревьев
100 % –Х деревьев
Отсюда находим количество деревьев в саду
Х=100*48/16=300 (деревьев).
Задача 10. (544) За два дня был проложен кабель. За первый день проложили 56% кабеля, а за другой - на 132 м меньше, чем первого. Сколько всего метров кабеля было проложено за два дня?
Решение: Задача похожа на предыдущую. За второй день проложили
100-56=44%
кабеля, разница между первым и вторым днем составляет
56-44=12%
и составляет 132 метра.
На основе этого составляем отношение
12% – 132 м
100 % –Х м
Отсюда находим искомую длину
Х=100*132/12=1100 (м.)
За два дня проложили 1100 м.. кабеля.
Задача 11. (545) За первый день мальчик прочитал 25% всей книги, за второй - 72% от количества страниц что осталась, а за третий - остальные 84 страницы. Сколько страниц в книге?
Решение: 72 % процента от остатка книги составляет
72*(100-25)/100= 54%.
На третий день оставалось прочитать
100-25-54=21%
или 84 страницы.
Составляем соотношение
21% – 84 ст
100 % –Х ст
с которого находим
Х=100*84/21=400 (ст),
что книга содержит 400 страниц.
Сложные задачи на простые проценты
В данную категорию входят задачи , которые вызывают немало трудностей у школьников. Однако , если достаточно хорошо разобраться в их решении, то все сложности отходят на второй план.
Задача 12. (547) Морская вода содержит 5% соли. Сколько пресной воды нужно добавить к 40 кг морской воды, чтобы концентрация соли составляла 2% ?
Решение: Находим вес соли в 40 кг морской воды
40*5/100=2 (кг).
Находим вес воды, которая содержала 2% соли (2 кг)
2% – 2 кг
100 % –Х кг
или
Х=100*2/2=100 кг.
Сейчас у нас есть 40 кг воды, поэтому нужно добавить
100-40=60 кг
пресной воды.
Задача 13. (554) Перемешали 30- процентный раствор соляной кислоты с 10- процентным раствором и получили 800 г 15 - процентного раствора. Сколько граммов каждого раствора взяли для этого?
Решение: В таких задачах требуется составить два уравнения, решение которых и приведет к отысканию нужных величин.
Обозначим A – вес первого раствора, B – соответственно второго.
Тогда из условия задачи составляем два уравнения:
первый касается процентных соотношений ( * 100 )
30*A+10*B=800*15
второе - веса смеси
A+B=800.
С второго выражаем одну из неизвестных и подставляем в первое уравнение
A=800-B;
30*(800-B)+10*B=800*15
и решаем его
24000-30*B+10*B=12000;
20*B=24000-12000=12000;
B=12000/20=600 (г).
Массу первого раствора находим из зависимости
A=800-B=800-600=200 (г).
Следовательно, нужно 600 г 30% раствора и 200 г 10% раствора соляной кислоты.
Задача 14. (560) К сплаву меди и цинка, содержащему меди на 12 кг больше, чем цинка, добавили 6 кг меди. Вследствие этого содержание цинка в сплаве снизилось на 5%. Сколько цинка и сколько меди содержал сплав в самом начале?
Решение: Обозначим вес меди через X, тогда вес цинка – X-12.
Процентное содержание цинка при этом составляет
(X-12)/(X+X-12)*100%=(X-12)/(2*X -12)*100%.
К сплаву добавили 6 кг меди. Вес меди теперь составляет X+6,
а сплава
X+6+X-12=2*X-6.
Процентное содержание цинка в новом сплаве
(X-12)/(2*X-6)*100% .
Разница между предыдущим сплавом и новым составляет 5%. Это запишем в виде уравнения
Делим данную запись на 100%
и сводим к квадратному уравнению (избавляемся знаменателей)
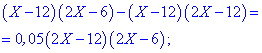
Упрощаем левую часть уравнения
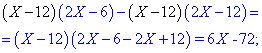
и правую
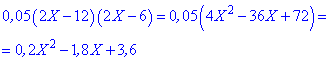
После переноса слагаемых в правую сторону, получим квадратное уравнение
Вычисляем дискриминант
и корни уравнения
Итак имеем не единое, а пару решений. При 21 кг меди получим цинка
X-12=21-12=9 (кг) ,
а при 18 кг меди
X-12=18-12=6 (кг).
Итак возможны два сплавы - 9 кг цинка и 21 меди, 18 кг цинка и 6 меди. Можете убедиться, что при подстановке в процентное уравнения первый сплав будет содержать 30% цинка, а второй - 25% цинка.
Подобных задач Вы встретите в литературе немало. Задачи на проценты требуют от Вас только хорошо разобраться, что известно? и что нужно найти? Все остальное сводится к простым математическим действиям.
