Продовжуємо урок на тему Логорифмічні рівняння і далі проаналізуємо відповіді на завдання із курсу ЗНО підготовки.
Хто готується до ДПА усі наведені приклади може також використати в навчанні.
Усі приклади, що далі йдуть - це логарифмічні рівняння звідні до квадратних.
Приклад 21.9 Розв'яжіть рівняння:
15. Виписуємо ОДЗ обох логарифмів та прирівнюємо вирази:
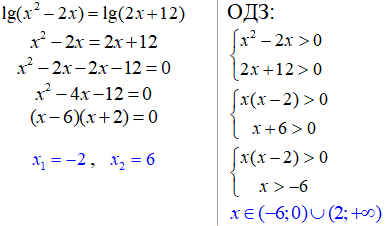
16. В окремих завданнях де з'ясування ОДЗ трудомістке достатньо виписати самі умови, а після розв'язання логарифмічного рівняння перевірити чи всі корені належать ОДЗ.
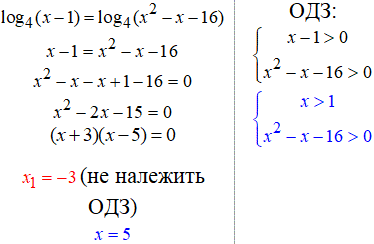
17. Наступне рівняння з логарифмами має два розв'язки, але жоден не задовільняє область допустимих значень.
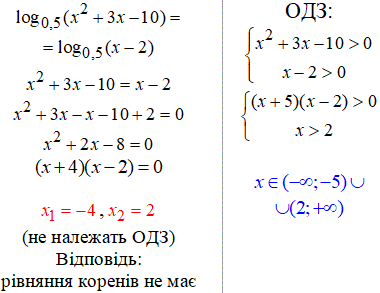
18.
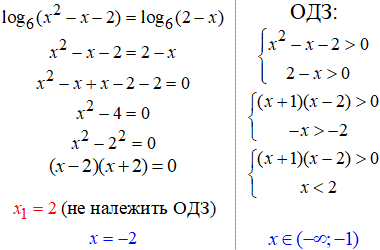
19. При обчисленні логарифмічних рівнянь нас мало цікавить чи більша за одиницю основа, а чи менша (як в цьому прикладі).
Це не логарифмічні нерівності, що там змінюється знак при розкритті, якщо основа менша одиниці.
Тому наступного виду рівнянь Ви не повинні боятися, розкриваємо логарифми за правилами як для всіх попередніх прикладів.
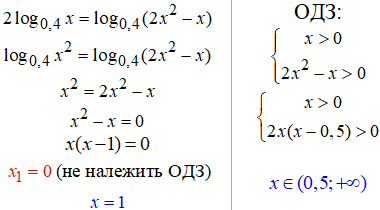
20. Щоб отримати однакові логарифми множник перед логарифмом вносимо в логарифм.
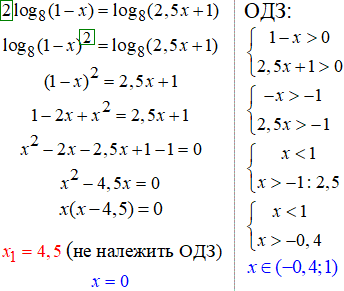
21. Уважно зіставляйте розв'язки логарифмічного рівняння з тим, що маєте в ОДЗ.
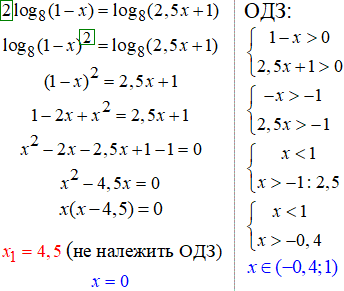
22.За властивістю:
Сума логарифмів рівна логарифму добутку виразів під логарифмами.
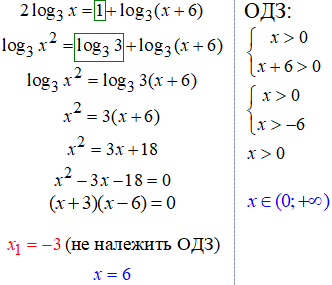
Приклад 21.13 Знайти розв'язки логарифмічного рівняння:
23. Сумуємо логарифми та спрощуємо логарифмічне рівняння
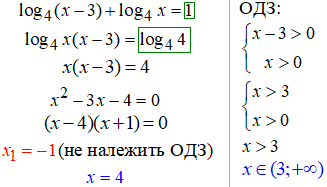
24. Справа маємо -1, а це рівно логарифму основи в мінус першому степені.
Оскільки основа рівна 0.5, то 0.5^(-1)=(1/2)^(-1)=2.
Це ми використали при перетворенні правої частини рівняння:
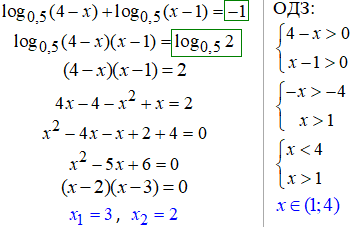
25. Зліва маємо суму логарифмів, справа - різницю логарифмів. За властивостями логарифма при перетворенні зліва отримаємо логарифм добутку, справа - логарифм частки:
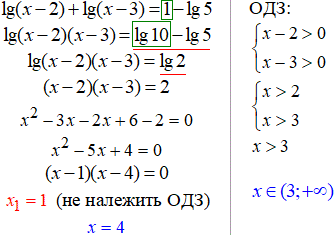
26.
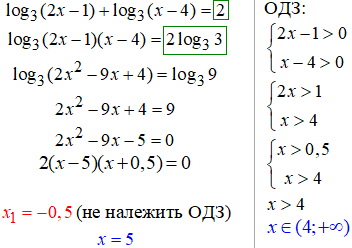
27. Під логарифмом маємо корені квадратні, їх записуємо як вирази під коренями в степені 1/2, а далі показники виносимо перед логарифми.
В правій стороні, щоб отримати 1/2 перед логарифмом беремо і підносимо до квадрата вираз під логарифмом.
Уважно прослідкуйте цей метод в формулах та використовуйте в подібних до цього завданнях.

28.

29. Різницю логарифмів перетворюємо до логарифма частки. Додаткових умов на знаменники дробів не слід виписувати, оскільки вони вже враховані в умовах на ОДЗ.
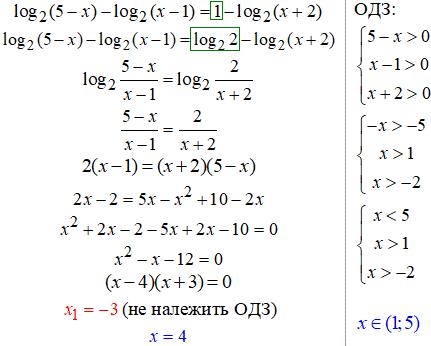
30. Тут маємо три логарифм, тому в ОДЗ отримаємо три умови, які обмежують множину розв'язків рівняння.
А далі опускаємо логарифми, а все що отримали зводимо до квадратного рівняння.
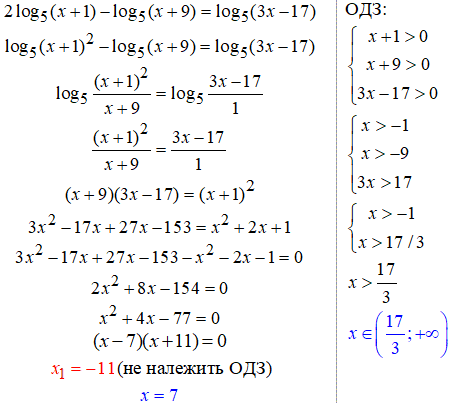
Корені ми підібрали за теоремою Вієта. На практиці не завжди це буде можливо, тому повторіть як обчислювати квадратне рівняння через дискримінант.
Сподіваємось, що матеріал Вам сподобався, а основні властивості логарифмів та методи обчислення логарифмічних рівнянь Ви запам'ятаєте надовго.


