Арифметичні приклади на числа

Посібник для підготовки до зовнішнього незалежного тестування з математики

Відповіді до посібника для підготовки до ЗНО тестування допоможуть Вам швидко пройти шкільний матеріал, пригадати усі теми, що можуть чекати Вас та скласти тести з успішним результатом.

Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж

Завантажити (скачати) відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики). Формат: PDF
Зміст: Посібник містить поради щодо проходження ЗНО з математики та взірці тестових завдань.
Усі задачі однієї теми розміщені в порядку складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.

Рік випуску: 2010 р.

Тема 1. Арифметичні приклади та задачі

Приклад 1.1 Яке з наведених чисел кратне числу 9?

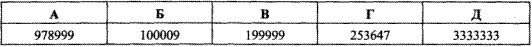
Обчислення: Даний розділ містить багато простих на перший погляд завдань, тому де це непотрібно, коментарів буде мінімум.
Тут скористаємося ознакою подільності на 9
2+5+3+6+4+7=27,
27:9=3.
Відповідь: 253647 – Г.

Приклад 1.2 Знайти найбільший спільний дільник чисел 42 і 63.

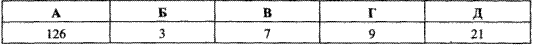
Обчислення: Розкладемо на множники задані числа:
42=2•3•7;
63=3•3•7.
Спільні множники складуть найбільший спільний дільник
Звідси НСД(42,63)=3•7=21.
Відповідь: 21 – Д.

Приклад 1.3 Знайти найбільший спільний дільник чисел 28 і 35.

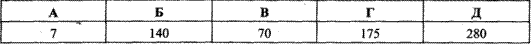
Обчислення: Розкладемо на множники задані числа:
28=2•2•7,
35=5•7.
Звідси знаходимо
НСД(28,35)= 2•2•5•7=140.
Відповідь: 140 – Б.

Приклад 1.4 Обчислити 1,521:0.3-1.9•0.3.

Обчислення: Спростимо вирази та знайдемо їх значення
1,521:0.3=15.21:3=5.07,
1.9•0.3=0.57,
5.07-0.57=4.5
Відповідь: 4,5 – Г.

Приклад 1.5 Обчислити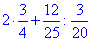

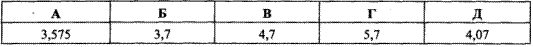
Обчислення: Виконуємо спрощення та ділення дробів

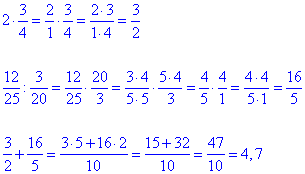
Знаходимо відповідне значення в тестах.
Відповідь: 4,7 – В.

Приклад 1.6 Обчислити .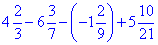

Обчислення: Зводимо дроби до спільного знаменника

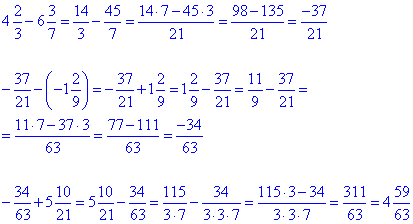
Подальші розрахунки під силу проаналізувати кожному випускникові школи.
Відповідь: 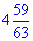– В.

Приклад 1.7 Обчислити -4.8(-2.6+3.4)+0.8.

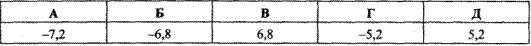
Обчислення: Просумуємо внутрішню частину дужки, а далі обчислимо значення виразу
-2.6+3.4=0.8,
-4.8:0.8=-48:8=-6,
-6+0.8=-(6-0.8)=-5.2.
Відповідь: -5.2 – Г.

Приклад 1.8 Знайти невідомий член пропорції (5x-7):12=2:3.

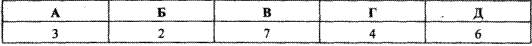
Обчислення: Основна властивість пропорції: добуток крайніх членів дорівнює добутку середніх членів, тобто a:b=c:d, або 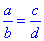, звідси
a•d=b•c.
(5x-7)•3=12•2,
3•(5x-7)=24,
отримали рівняння, розв'яжемо його відносно x
5x-7=24:3,
5x-7=8,
5x=8+7,
5x=15,
x=15:5,
x=3.
Відповідь: 3 – А.

Приклад 1.9 Вказати найбільше з наведених чисел.

Обчислення: Розпишемо числа відповідно до правил скорочених записів
0.23=0.23000…,
0.233=0.233000…
0,(23)=0,232323…,
0,2(3)=0,23333…
звідси видно, що
0,2(3)>0,(23)>0,233>0,23;
0,2(31)=0,2313…
звідси видно, що 0,2(3)>0, 2(31).
Отож, 0,2(3) є найбільшим серед наведених чисел.
Відповідь: 0,2(3) – Г.

Приклад 1.10 Вказати звичайний дріб, який дорівнює дробу 0,1(3).

Обчислення: Перетворимо десятковий запис дробу до звичайного (у вигляді частки чисел)

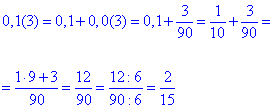
Правильний варіант містить 5 комірка тестових відповідей.
Відповідь: 2/15 – Д.

Приклад 1.11 Розкрити модуль |Pi-4|=

Обчислення: Відомо, що Pi=3.14, тому Pi-4<0, але модуль числа – невід'ємне число, тому
|Pi-4|=-(Pi-4)=4-Pi
Відповідь: 4-Pi – Г.

Приклад 1.12 Не виконуючи ділення, встановити остачу від ділення 33333333341 на 9.

Обчислення: Оскільки число містить дев'ять трійок (які націло діляться на 9), то остачу від ділення на 9 знайдемо для числа 41:
41=36+5=9•4+5.
Отож, остача від ділення числа 33333333341 на 9 дорівнює 5.
Відповідь: 5 – Б.