Логарифмічні рівняння. ЗНО підготовка

Продовжуємо вивчати усі можливі способи розв'язання логарифмічних рівнянь і сьогодні розберемо відповіді до завдань із ЗНО підготовки з математики.
Позбуватися логарифма у більшості з наведених рівнянь допоможе властивість, що логарифм основи рівний одиниці.
Водночас в правій частині будемо виписувати область допустимих значень (ОДЗ), виходячи з обмежень на логарифм:
log_a f(x)
вираз під логарифмом має бути більший від нуля;
f(x)>0
основа більша нуля та не рівна одиниці
a > 0, a ≠ 1.
На цьому і базуються усі перетворення, що Ви далі побачите.

Приклад 21.1 Розв'яжіть рівняння: 
1. Щоб звести праву сторону під логарифм з потрібною основовою слід застосувати властивість log[a](a)=1:

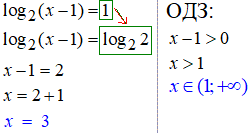
2. Властивість Ви швидко запам'ятаєте, всюди у формулах ми на ній наголошуємо, щоб Ви швидше навчилися її застосовувати на практиці.

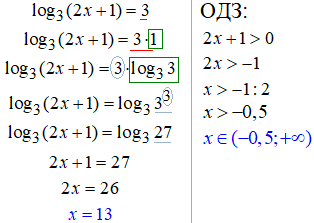
3.

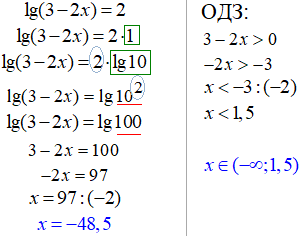
4. За властивістю логарифма множник перед логарифмом можна внести під логарифм як показник виразу під логарифмом.
Далі підносимо до степеня та прирівнюємо вирази під логарифмом справа та зліва від знаку рівності:

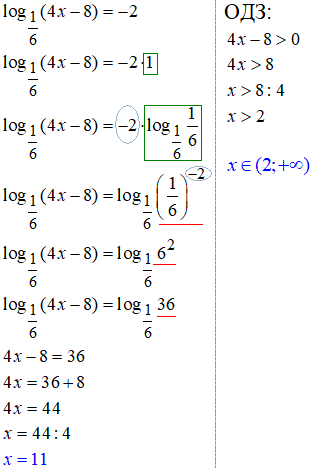
5. Далі розглянемо кілька завдань, де в результаті прирівняння логарифмів приходимо до розв'язування квадратних рівнянь.

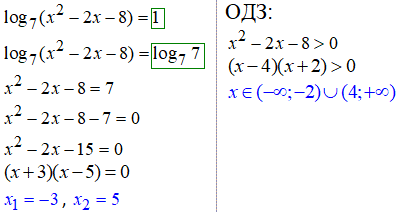
6. В розглянутому прикладі та наступних можна знаходити корені квадратного рівняння як через дискримінант, так за допомогою теореми Вієта.

Якщо корені легко підібрати, то застосування формул Вієта більш доцільно, оскільки час виконання ЗНО тестів зменшується.

Приклад 21.3 Знайти розв'язки рівнянь:
7. Не зважайте, що тут під основою маємо число Pi, наша задача виписати обмеження на ОДЗ логарифмів та прирівняти вирази під логарифмами:

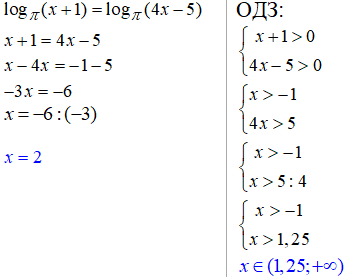
8.Справа та зліва від знаку рівності маємо логарифм, тому в таких прикладах виписуємо ОДЗ та прирівнюємо вирази під логарифмами.

9. Порівнюючи вирази під логарифмами, прийдемо до квадратного рівняння, яке розв'язуємо за формулами Вієта:

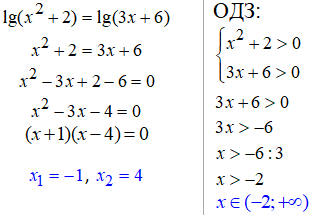
Пам'ятайте, що -1>-2, бо можете помилково відкинути один з розв'язків логарифмічного рівняння.

Приклад 21.5 Розв'язати рівняння:
10, 11.При обчисленні крім розглянутих вже властивостей логарифма додається ще одна:
різниця логарифмів рівна логарифму частки.
Як це відбивається на обчисленнях дивіться у формулах до наступного прикладу:

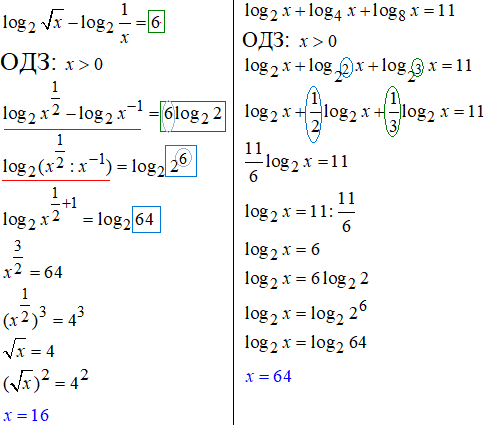
12, 13Якщо маємо різні основи, але частину з них можна подати як найменшу з основ в певному степені, то за властивістю логарифма степінь основи можна винести перед логарифм:
log_a^b f(x)= 1/b* log_af(x).
На практиці отримаємо:

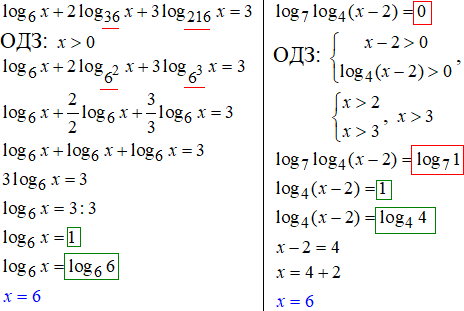
14. Уважно перегляньте як обчислювати три вкладені логарифми:
Якщо маємо вложені логарифми, то ОДЗ накладаємо на всі вирази під логарифмом, а не тільки на той, що має змінну під логарифмом:

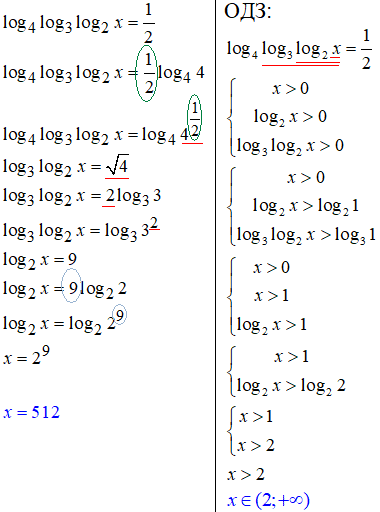
Решту готових прикладів на рівняння з логарифмами розберемо на наступному уроці.