Приклади обчислення показникових рівнянь

Сьогодні розберемо пояснення до прикладів на показникові рівняння, вияснимо на що слід звертати увагу в обчисленнях та основні алгоритми розкриття таких рівнянь. Приклади відібрані із збірника підготовки до ЗНО тестів, тож містять завдання, які учні розв'язують в 10, 11 класі та дещо складніші.
Для перевірки теоретичних знань спершу перегляньте основні формули показникових функцій

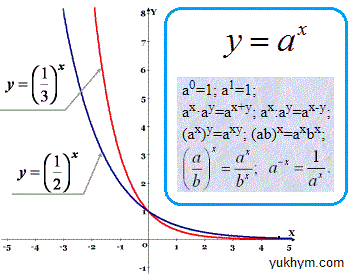
Якщо не забули теорії і формул, можете переходити до розв'язків завдань.

Приклад 14.4 Розв'язати рівняння 3^x-5=9^-2x.

Розв'язування: За допомогою елементарних перетворень добиваємося рівних основ, після чого прирівнюємо степені:
3^x-5=9^-2x,
3^x-5=(3²)^-2x,
3x-5=3-4x,
x-5=-4x,
x+4x=5,
5x=5,
x=5:5=1.
Відповідь: 1 – Б.

Приклад 14.5 Розв'язати рівняння

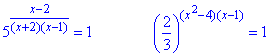
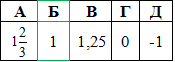
та вказати їх спільні корені.

Розв'язування: З аналізу показникових функцій зауважуємо, що перша в показнику містить дріб, знаменник якого не повинен перетворюватися в нуль. Це і є обмеженням на область допустимих значень (ОДЗ):
(x+2)(x-1)≠0,

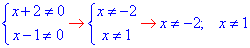
Одиниці в правій частині рівнянь за властивостями показникових функцій заміняємо основою в нульовому степені. А далі при рівних основах прирівнюємо степені та розв'язуємо отримані лінійне та квадратне рівняння:

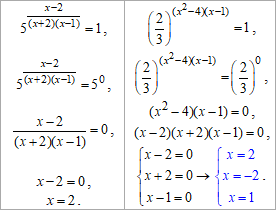
Враховуючи ОДЗ, спільним коренем обох рівнянь є 2.
Відповідь: 2 – Д.

Приклад 14.6 Якому з проміжків належить корінь рівняння 0,008^x=5^(1-2x)?

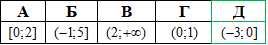
Розв'язування: Спростимо 0,008 до основи =5:

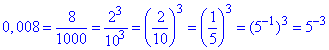
Підставимо у рівняння та прирівняємо степені

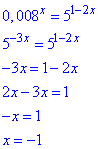
Отриманий корінь x=-1 належить проміжку (-3;0].
Відповідь: (-3;0] – Д.

ЗНО_Приклад 14.7 Серед наведених рівнянь вказати рівняння, рівносильне рівнянню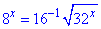

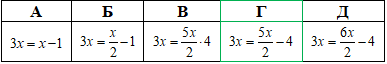
Розв'язування: Перетворимо праву сторону за знаком рівності до основи =2:

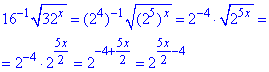
Представимо 8 як двійну в кубі, та при рівних основах прирівнюємо показники

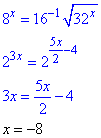
Отримали лінійне рівняння відносно невідомої, яка після обчислень рівна x=-8.
У відповідях до тестів рівняння 3x=5x/2-4 міститься в пункті Г.
Відповідь: 3x=5x/2-4 – Г.

Приклад 14.32 Розв'язати рівняння

Розв'язування: В показнику двійки маюмо корінь квадратний зі змінної, тому вона повинна приймати невід'ємні значення:
ОДЗ: x≥0.
Далі загальновідома методика обчислень:
найменший спільний множник, що містить змінну виносимо за дужки, а все решта згруповуємо та переносимо до сталої в праву сторону.
Тоді при рівних основах виписуємо показники, та у нашому випадку розв'язуємо рівняння з коренем.

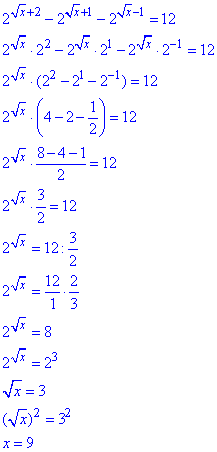
Відповідь: 9.

Приклад 14.41 Розв'язати рівняння

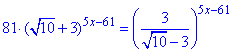
Розв'язування: Щоб спростити рівняння спершу перемножимо вирази з однаковими степенями та, з використанням формули різниці квадратів, спростимо знаменник. В такий спосіб отримаємо просте показникове рівняння, яке обчислюємо співставленням степенів.

Формул багато, але це не є одні з важчих завдань, що Ви можете бачити на ЗНО тестах.
Найважчі приклади ми згрупували в окрему статтю, яка чекає Вас попереду.
Відповідь: 13.

Приклад 14.14 Розв'язати рівняння

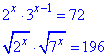
і вказати суму їх коренів.

Розв'язування: В першому та другому рівнянні групуємо множники, які мають спільні найменші степені. Все що залишиться переносимо в праву сторону та зводимо до основи вигляду 6^ та 14^. При рівних основах прирівнюємо показники та обчислюємо "ікси":

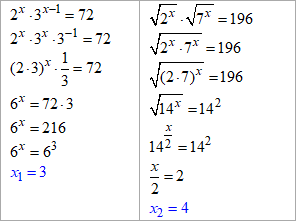
x₁+x₂=3+4=7 – сума коренів рівнянь.
Відповідь: 7 – Б.

Приклад 14.23 Знайти суму коренів рівняння (x²+x+1)^x-3=1.

Розв'язування: Запам'ятайте даний тип показникових рівнянь, адже їх обчислюють за наступним алгоритмом.
З вигляду рівняння зауважуємо, що права частина рівна одиниці. Для показникових функцій це можливо лише у двох випадках, або основа рівна одиниці або степінь рівний нулю. Тому задане р-ня рівносильне двом наступним:

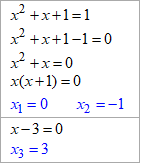
Звідси x₁=0, x₂=-1, x₃=3 – розв'язки рівняння.
Обчислимо суму коренів:
x₁+x₂+x₃=0-1+3=2
Відповідь: 2 – Г.

Приклад 14.25 Установити відповідність між рівняннями (1–4) та кількістю їх коренів (А – Д).

Розв'язування: Усі рівняння в основі мають двійку, причому 3 з 4 рівнянь в показнику містять змінну під знаком модуля, тому при розкритті модулів можуть ділитися на 2 випадки. Уважно перегляньте схему обчислень такого плану прикладів:


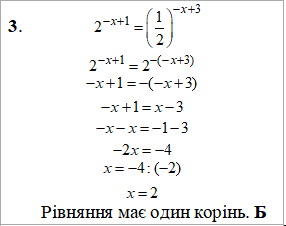
Як бачите, нічого надскладного тут не виконували, всі операції "як книжка пише".

Приклад 14.21 Розв'язати рівняння 2^sin²(x)+2^cos²(x)=3.

Розв'язування: Використаємо тригонометричну тотожність:
cos²(x)=1-sin²(x)
щоб перетворити показник в другому рівняння, та звести рівняння до квадратного

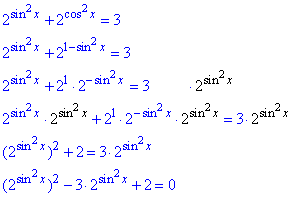
Заміна змінних:
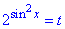, де t>0, тоді t²-3t+2=0.
За формулами Вієта записуємо:
t₁+t₂=3 – сума коренів рівняння та
t₁•t₂=2 – їх добуток.
t₁=1 і t₂=2 – розв'язки.
Повертаємося до заміни змінних 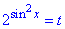та розписуємо:

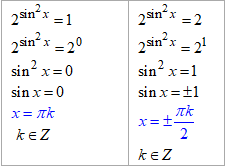
Корінь рівняння x=πk/2, k∈Z в собі вже містить корінь x=πk (якщо k набуватиме парних значень) і корінь x=-πk/2 (якщо k набуватиме від'ємних значень).
Тому x=πk/2, k∈Z – множина розв'язків рівняння.
Відповідь: x=πk/2, k∈Z – Д.

Приклад 14.30 Розв'язати рівняння

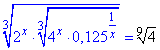
У відповідь записати суму коренів рівняння.
Розв'язування: Маємо два вложені кубічні корені від виразів, що містять змінну.
Можна виписати ОДЗ на кореневі функції: x≠0, однак права частина додатна і розв'язок точно існує.
Залишається перетворити вирази у кожній частині рівняння до показникової форми зі спільною основою:

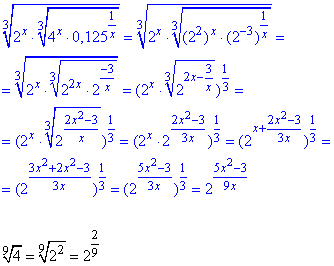
Після підстановки прирівнюємо степені

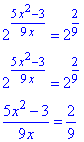
Помножимо обидві частини рівняння на 9, та знайдемо корені квадратного рівняння через дискримінант

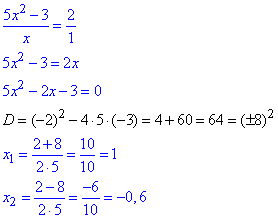
За умовою, сумуємо значення:
x₁+x₂=1+(-0,6)=0,4.
Відповідь: 0,4.

Приклад 14.38 Розв'язати рівняння 2^cos(2x)=3•2^(cos₂(x)-4).
У відповідь записати x0/π, де x0 – найменший додатний корінь рівняння.
Розв'язування: В показнику маємо косинус квадратний та косинус подвійного кута, останній заміняємо за допомогою тригонометричної формули
cos(2x)=1-2•cos²(x).
Запам'ятайте цей момент, адже без знання цієї формули Вам рівняння ніяк не вдасться спростити.
Підставляємо в показник та розписуємо:

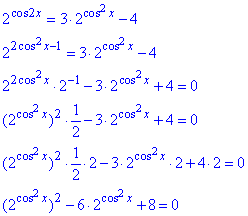
Заміна змінних 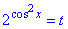, де t>0, дозволяє звести задане р-ня до обчислення коренів квадратного р-ня
t²-6t+8=0.
які знаходимо за формулами Вієта:
t₁+t₂=6,
t₁•t₂=8.
Легко підібрати значення
t₁=2, t₂=4.
Далі повертаємося до заміни та прирівнюємо показники, вони дають нам два тригонометричні рівняння, які розписуємо:

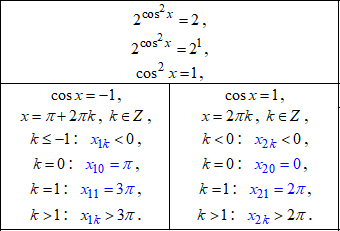
x₀=π – найменший додатний корінь рівняння, звідси
x₀/π=π/π=1.
Відповідь: 1.

Решта готових відповідей  чекають на Вас в наступних публікаціях.