Метод логарифмування. Показникові рівняння з різними основами

Рівняння з різними основами виду a^f(x)=b^g(x) розв'язують шляхом логарифмування рівняння за основою, що містить змінну в показнику:
log_aa^f(x)=log_ab^g(x);
f(x)=g(x)·log_ab.
Останнє, як правило, легко обчислювати. Слід зауважити, що додатково потрібно виписувати умови на ОДЗ функцій.
Наведемо таблицю основних властивостей показникових функцій

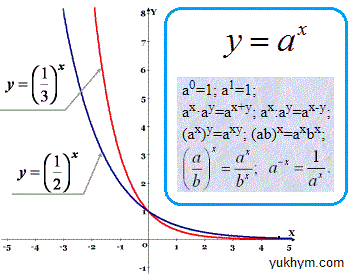
До цих формул Ви можете повернутися в будь-який момент, а зараз перейдемо до готових відповідей з курсу ЗНО підготовки. 

Приклад 14.10 Розв'язати рівняння
4^x+2-4^x+1+4^x=39

Розв'язування: Виносимо найменший спільний множник для показникових виразів і сумуємо множники при них. Далі на отриману суму ділиму праву сторону рівняння, в результаті зводимо розрахунки до простого показникового рівняння з різними основами. Щоб його розв'язати застосовуємо метод логарифмування:

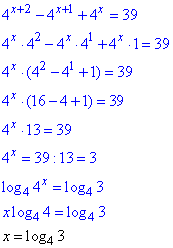
За основу при логарифмуванні вибирають число (див. пояснення далі), яке піднесено до степені, що містить змінну =4.
Логарифм основи рівний одиниці, а степінь виносимо перед логарифм множником.
Відповідь: log₄3 – Г.

Приклад 14.13 Розв'язати рівняння 7^x²=2.

Розв'язування: Бачимо, що основи рівняння не рівні між собою, хоча рівяння на вигляд просте. Прологарифмуємо обидві частини за основою 7, після цього розв'яжемо отримане неповне квадратне рівняння:

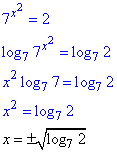
Округлений корінь рівний 0,3562.
Варто зауважити, що логарифм приймає і від'ємні значення тому перш ніж його вносити під корінь слід перевірити знак.
В курсі підготовки до ЗНО тестів є багато прикладів, відповіді яких містять суперечливі трактування.
Про це в нас є окрема стаття, яка вчить на що слід звертати уваги при проходженні вступних екзаменів, тестів, олімпіад.
Відповідь: 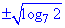– В.

Приклад 14.8 Яке з наведених рівнянь має корені?

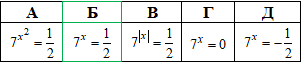
Розв'язування: 1. Права частина усіх варіантів рівна 1/2, ліва містить 7 в різниках показниках. Єдиним методом розкритття такого плану рівнянь є логарифмування за основою (7) обох його частин. В результаті отримаємо:

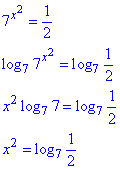
Багато з Вас роблять помилку і записуть корінь квадратний з логарифма як розв'язок без аналізу, але це не правильно.
Спершу потрібно оцінити, що ми дістали в результаті обчислень. І є одне «но», логарифм в правій частині може бути від’ємний, а в лівій маємо квадратичну функцію, яка для усіх значень крім нуля додатна.
log_ab>0, якщо 0<b<1 і a>1.
Оскільки для будь-яких x маємо x²>0 і log⁷(1/2)<0, то рівняння коренів не має.
Не забувайте виконувати перевірку цієї умови!

2. Прологарифмуємо рівняння

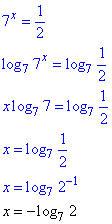
Отримали один розв’язок рівняння.
На цьому на ЗНО тестах  необхідно зупинитися, потрібне рівняння, що має корінь ми знайшли.

3. Розпишемо додатково останні приклади, щоб показати Вам, наскільки легко логарифмувати

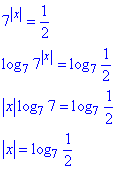
Проста перевірка показує, що модуль змінної x додатний |x|>0, в той час як логарифм від'ємний log₇(1/2)<0, тому рівняння коренів не має.

4. 7^x=0.
З властивостей показникових функцій, ви повинні знати, що вони приймають додатні значення a^x>0, якщо основа додатня a>0, в нас же права сторона =0.
Тому приймаємо висновок, що рівняння коренів не має.

5. 7^x=-1/2.
Ще одне завдання на знання степеневих функцій:
a^x>0, якщо a>0, тому рівняння коренів не має.
Відповідь: 7^x=1/2 – Б.

Приклад 14.24 Установити відповідність між рівняннями (1–4) та їх коренями (А – Д). 

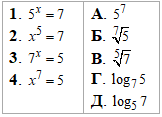
Розв'язування: Задані прості показникові рівняння, два з яких розв'язуємо логарифмуванням. В двох інших рівняннях застосовуємо корінь 5 та 7 порядку, щоб знайти "ікс".

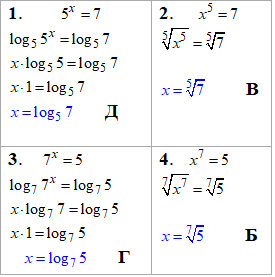
Так як корені непарних степенів, то права частина могла б бути і від'ємною.
Для парних степенів це недопустимо.
Пам'ятайте про це при обчисленнях.

Приклад 14.40 Розв'язати рівняння

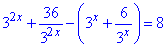
У відповідь записати найбільший корінь рівняння.
Розв'язування: Спершу розпишемо, щоб отримати вираз у других дужках у квадраті з перших двох доданків.

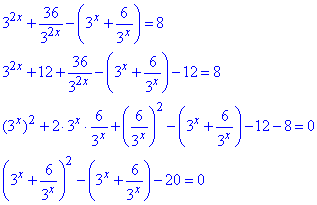
заміна: 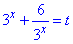, де t>0.
Після підстановки, корені квадратного рівняння
t²-t-20=0.
визначаємо за формулами Вієта:
t₁+t₂=0,
t₁•t₂=-20.
Звідси, t₁=-4<0 (не задовільняє ОДЗ),
t₂=5.
Повертаємося до заміни і повторно зводимо показникове рівняння до квадратного

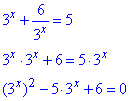
заміна: 3^x=u, де u>0.
u²-5u+6=0.
Використаємо теорему Вієта:
u₁+u₂=5,
u₁•u₂=6.
Звідси u₁=2, u₂=3.
Повертаємося до заміни і розв'язуємо рівняння, що дістали шляхом логарифмування

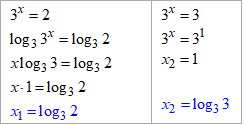
Оскільки log₃3>log₃2, і функція y=log₃x зростає на всій області визначення, то x₂>x₁, тому x₂=1 – найбільший корінь заданого рівняння.
Відповідь: 1.

Останнє рівняння показує, наскільки громіздкими бувають розрахунки складних показникових рівнянь. Уважно перегляньте пояснення і зробіть висновок, що властивості показникових функцій та логарифмів потрібно добре знати, в іншому випадку Ви не зможете довести обчислення до правильної відповіді.