Дана стаття присвячена не стільки обчисленню показникових рівнянь, як навчанню абітурієнтів:
на що слід звернути увагу при проходженні ЗНО тестів?
та де Ви допускаєте помилки? і через що?
Усі Ви думаєте, що репетитори вас і так цього навчать, але дочитавши відповіді з курсу ЗНО підготовки до кінця більша половина з Вас точно поміняє свою думку.
Приклад 14.15 Розв'язати рівняння
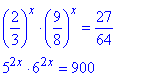
та вказати суму їх коренів.
А | Б | В | Г | Д |
8 | 7 | 6 | 5 | 4 |
Розв'язування: Перемножуємо числа в однакових степенях і до такої ж основи в певному степені розписуємо праву сторону рівнянь.
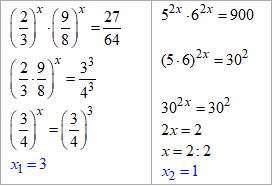
Сумуємо x1+x2=3+1=4 – корені рівнянь.
Відповідь: 4 – Д.
На перший погляд досить прості та зрозумілі усім обчислення, та перегляньте наступні відповіді.
Приклад 14.16 Знайти значення виразу 7x з рівняння
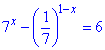
А | Б | В | Г | Д |
1 | 2 | 6 | 7 | 14 |
Розв'язування: Обчислення розпочнемо з того, що 1/7 представимо як 7-1, далі 7х винесемо з перших двох доданків, а все що залишиться дільником переносимо в праву сторону. Далі при однакових основах прирівнюємо степені:
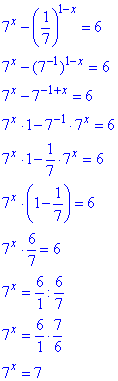
Розв'язок рівний x=1, але нас цікавить не він. А основа в степені розв'язку 71, уважно перечитайте умову.
На ЗНО тестах таких завдань багато, хоча, на нашу думку, не мало би так бути. Ви зосереджені, щоб до кінця розписати, а це може виявитися зайвим.
Тому Ви можете добре знати тему, а Вам будуть "зрізати" бали, тому що наверху вирішили намудрувати з умовами.
Відповідь: 7 – Г.
Приклад 14.17 Знайти значення виразу (2/3)х, якщо
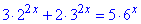
А | Б | В | Г | Д |
4 | 3 або 4 | 2/3 або 1 | 0 або 1 | 4/9 або 1 |
Розв'язування: Завжди аналізуйте, що конкретно потрібно визначити. Добре розуміння умови досить часто позбавляє від лишніх рухів наприкінці розрахунків.
Оскільки нам потрібно знайти (2/3)х, то саме до рівняння з множниками кратними (2/3)х зведемо задане. А для цього розділимо його на 32х та спростимо
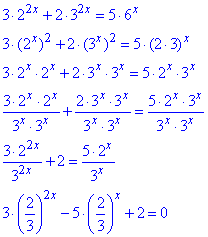
Отримали квадратне рівняння відносно шуканої величини (2/3)х.
Виконуємо заміну: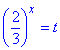 , причому не забуваємо записувати умову обмеження на ОДЗ: t>0.
, причому не забуваємо записувати умову обмеження на ОДЗ: t>0.
Рівняння 3t2-5t+2=0 розв'язуємо через дискримінант
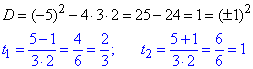
На цьому обчислення завершені.
Ті хто захоче показати, що він багато знає і вміє, повернеться до заміни t=(2/3)х, підставить t1=2/3 та t2=1 і врезультаті отримає розв'язки x1=1, x2=0.
Такий варіант теж є в ЗНО відповідях (Г), тільки за нього Ви не отримаєте потрібні для вступу бали.
Будьте уважними, та завжди готові до реалій!
Відповідь: 2/3 або 1 – В.
Приклад 14.18 Знайти значення виразу 2x, якщо 2(2-x)-2x-1=1.
А | Б | В | Г | Д |
2 | 2 або -4 | 1 | 4 | 2 або 4 |
Розв'язування: Спростимо рівняння , щоб зліва мати 2 в степені змінної, а далі ціле рівняння домножимо на 2•2x . В такий спосіб задане показникове рівняння зведемо до квадратного відносно 2x
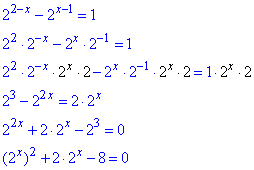
Заміна змінних:
2x=t, де t>0, тоді маємо
t2+2t-8=0.
За теоремою Вієта:
t1+t2=-2 – сума коренів квадратного рівняння;
t1•t2=-8 – їх добуток,
звідси знаходимо один розв'язок, який не задовільняє ОДЗ: t>0
t1=-4<0 і
t2=2 – шуканий корінь рівняння.
Повертаємося до заміни, щоб знайти «ікс»
2x=2 (тоді x=1).
І знову наголошуємо, гляньте в умову, що нам потрібно знайти.
Правильний варіант
21=2. А.
Хто на тестах віповість x=1 В заробить на ЗНО 0 балів.
Відповідь: 2 – А.
Приклад 14.26 Установити відповідність між парами рівнянь (1–4) та сумою їх коренів (А–Д).
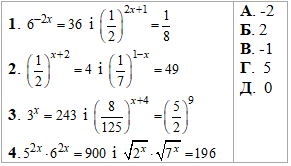
Розв'язування: Усі рівняння зводимо до спільної основи, далі прирівнюємо показники і знаходимо розв'язки.
Після цього обчислюємо суму коренів та співставляємо з відповідями ЗНО тестів.
Пояснення розберіть самостійно з наведених таблиць:
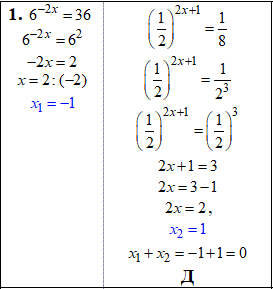
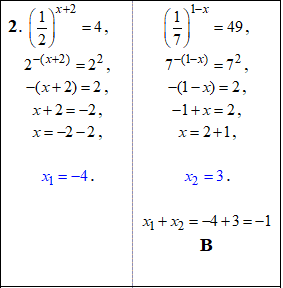
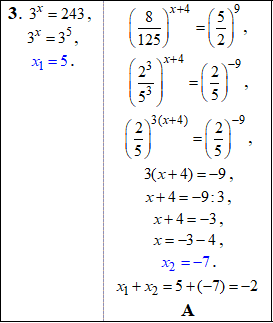
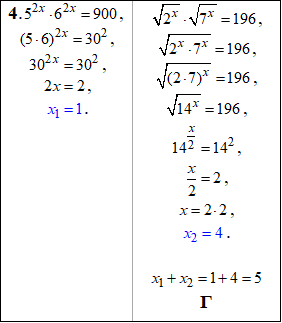
1 – Д, 2 – В, 3 – А, 4 – Г.
Думаю у Вас немає питань до обчислень, в інакшому випадку Вам необхідні індивідуальні заняття з репетитором.
Приклад 14.19 Знайти значення виразу 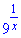 , якщо
, якщо 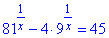 .
.
А | Б | В | Г | Д |
4 або 9 | -4 або 9 | 9 | 81 | 16 або 25 |
Розв'язування: Дослідивши рівняння робимо висновок, що його слід звести до квадратного рівняння:
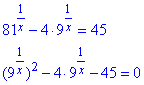
Виконаємо заміну змінних:
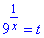 , де t>0, та підставимо її в останню формулу
, де t>0, та підставимо її в останню формулу
t2-4t-45=0.
За формулами Вієта: t1+t2=4 – сума коренів;
t1•t2=-45 – добуток коренів квадратного рівняння,
звідси шляхом перебору визначаємо t1=-5<0 і t2=9 – розв'язки рівняння.
Розписуємо показникове рвняння 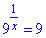 (тоді x=1).
(тоді x=1).
У відповідь записуємо 9 в степені кореня показникового рівняння, а не сам корінь.
УВАЖНО ЧИТАЙТЕ ЗАВДАННЯ, Що знайти!
Відповідь: 9 – В.
Приклад 14.27 Установити відповідність між рівняннями (1–4) та значеннями (А – Д) виразу 2x0-1, де x0-1 – корінь рівняння.
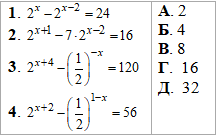
Розв'язування: Завдання спрощуємо шляхом винесення найменшого спільного множника (НСК), що містить змінну ( 2x) за дужки. Далі всі доданки , що при ньому залишилися додаємо і на цю суму ділимо праву сторону. Як правило, в результатті повинні отримати НСК (2) в певному степені. Якщо ні, Ви скоріш за все помилилися, або викладач намудрував з умовою і доведеться логарифмувати обидві частини рівняння, щоб отримати «ікси».
Пояснення, що і для чого робили розберіть самостійно з таблиць:
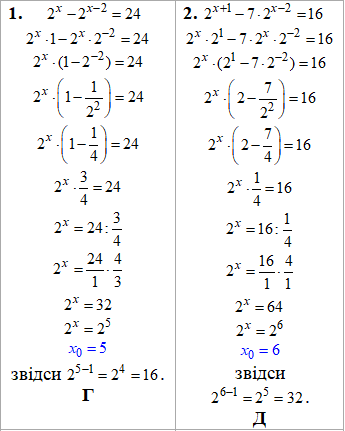

І якщо Ви не отримали одну з відповідей, що йдуть в таблицях під умовою, значить Ви десь накосячили.
Повторно перевірте хід своїх дій!
Приклад 14.33 Розв'язати рівняння
7·3x-5x+1=3x+3-5x+2
Розв'язування: Бачимо, що в обох частинах містяться комбінації двох чисел – 3 і 5, в показнику якихмаємо вирази залежні від x. Для зведення до простого типу групуємо доданки, які мають спільну основу, а далі на одне з чисел в степені змінної розділяємо обидві частини рівняння.
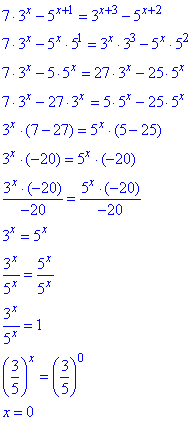
Вкінці розрахунків в правій стороні виділяємо 1= рівна будь-якій основі в 0 степені.
Розв'язок дорівнює нулю x=0.
Відповідь: 0.
Приклад 14.44 Знайти:
- найбільше значення виразу (2/3)^x;
- додатний корінь рівняння, якщо 3•2x+2•32x =5•6x.
Розв'язування: Розділимо на 32х та розпишемо до вигляду квадратного рівняння
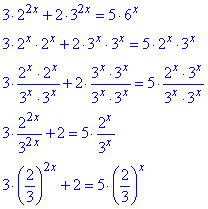
З кінцевої формули бачимо, що слід зробити заміну:
(2/3)x=t>0.
Після підстановки знайдемо через дискримінант корені отриманого рівняння
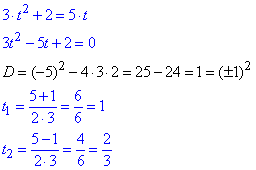
Їх підставляємо в зроблену заміну та розв'язуємо прості рівняння:
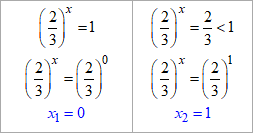
За умовою прикладу визначаємо найбільше значення виразу:
(2/3)1=2/3.
x2=1 – додатний корінь рівняння.
При такому оформленні ЗНО відповіді Ви отримаєте половину, можливо й більшу від загальної кількості балів.
Ми навмисне допустили помилку, перше значення знайдене неправильно. Це зроблено спеціально, щоб чогось та й навчити Вас.
Запам'ятайте, що при оснавах менше одиниці 2/3<1, якщо вираз підносити до степеня, то чим він менший, тим більше значення отримаємо.
Тому (2/3)1<(2/3)0 =1.
Відповідь: 1) 1; 2) 1.
Приклад 14.31 Розв'язати рівняння
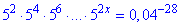
Розв'язування: Згрупуємо степені у першій частині рівняння:
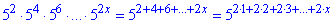
У показнику маємо арифметичну прогресію (an),
де a1=2 – перший член,
d=2 – різниця,
n=x – номер (кількість) членів прогресії.
Зауважимо, що n=x – натуральне число, x>0.
Обчислимо суму арифметичної прогресії за формулою:
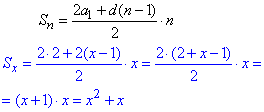
Підставимо суму Sx та спростимо рівняння
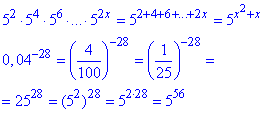
Основи рівні, прирівнюємо степені
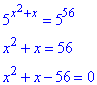
Отримали квадратне рівняння, розв'язки якого знаходимо за теоремою Вієта:
x1+x2=-1,
x1•x2=-56.
Звідси,
x1=-8
(не задовольняє умові про кількість членів арифметичної прогресії),
x2=7.
В підсумку, x=7 – єдиний корінь заданого рівняння.
Відповідь: 7.
Будьте уважні при розрахунках, неправильне трактування умови прикладів навіть при вірних обчисленнях приведе Вас до невірної відповіді. Цим корустуються не тільки на ЗНО тестах, за такою схемою підбирають завдання на олімпіади, контрольні і т.д.
Хто з Вас готується до вступу у ВУЗи або навчається в 10, 11 класі може переглянути сусідні статті з цієї теми, або й пройти увесь курс ЗНО підготовки.


