Звідні до квадратних показникові рівняння

Рівняння вигляду A•a^2f(x)+B•a^f(x)+C=0, шляхом заміни змінних t=a^f(x) можна звести до обчислення квадратного рівняння
A•t²+B•t+C=0.
Після знаходження коренів  t1, t2 повертаємося до заміни та розв'язуємо показникові рівняння простого типу:
a^f(x)=t1; a^f(x)=t2.
Це в теорії, а на практиці корені квадратного рівняння повинні бути додатними, якщо основа додатна a>0 + завжди в обчисленнях слід або виписувати область допустимих значень (ОДЗ) для a^f(x), або після обчислень перевірити підстановкою чи знайдені розв'язки показникового рівняння перетворюють його в тотожність.

Нагадаємо основні формули перетворення степенів, які Ви повинні знати для самостйного обчислення прикладів 

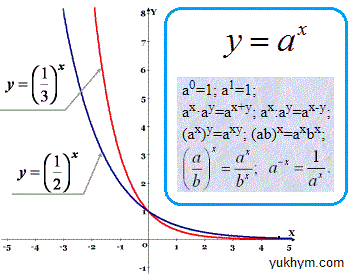
Далі йдуть пояснення до завдань з курсу підготовки до ЗНО, який загалом налічує понад 50 завдань по цій темі.

Приклад 14.20 Указати проміжок, якому належить корінь рівняння?


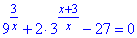
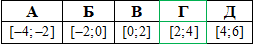
Розв'язування: Маємо показникове рівняння, звідне до квадратного. В степені 9 маємо дріб в знаменнику якого змінна, тому додатково записуємо умову ОДЗ: x≠0.
Спрощуємо рівняння:

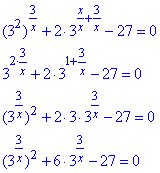
Заміна: t=3^(3/x), де t>0, тоді t²+6t-27=0.
За теоремою Вієта:
t1+t2=-6 – сума коренів;
t1•t2=-27 – їх добуток, звідси 
t1=-9<0 (не задовольняє ОДЗ) і t2=3 – розв'язки квадратного рівняння.
Повертаємося до заміни і обчислюємо показникове рівняння

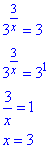
Його корінь x=3 належить проміжку [2;4].
Відповідь: [2;4] – Г.

Приклад 14.36 Розв'язати рівняння

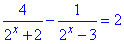
У відповідь записати суму коренів рівняння.
Розв'язування: З обмеження на знаменники дробів, що містять показникові вирази виписуємо умови на ОДЗ:
2^x+2≠0,
2^x≠-2.
Оскільки 2^x>0 для всіх x, то умова 2^x≠-2 на розв'язок рівняння не вливає.
2^x-3≠0
2^x≠3,
x≠log₂3.
Зводимо дроби до спільного знаменника та методом елементарних перетворень спрощуємо

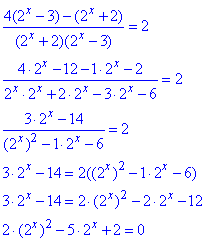
Бачимо готову форму квадратного рівняння при заміні змінних:
t=2^x, де t>0 і t≠3 (згідно з ОДЗ).
Обчислюємо дискримінант та корені рівняння

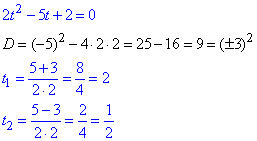
Далі повертаємося до заміни та розв'язуємо прості рівняння:
2^x=2,
2^x=2¹,
x₁=1.

2^x=1/2,
2^x=2^-1,
x₂=-1.
Наостанок, знаходимо суму 
x₁+x₂=1+(-1)=0.
Відповідь: 0.

Приклад 14.34 Розв'язати рівняння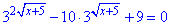

У відповідь записати суму коренів рівняння.
Розв'язування: Виписуємо ОДЗ для кореневих функцій:
x+5≥0, звідси x≥-5.
Далі перетворюємо до квадратного р-ня

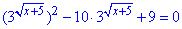
за допомогою заміни змінних:
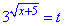, де t>0
t^2-10t+9=0.
За теоремою Вієта:
t₁+t₂=10,
t1•t2=9.
Звідси,
t₁=1, t₂=9.
Підставляємо знайдені t в 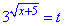  та за правилами розписуємо до рівнянь з коренями:

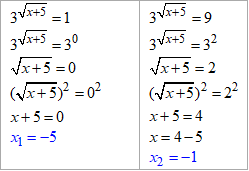
Обчислюємо суму
x₁+x₂=-5+(-1)=-6
Відповідь: -6.

Приклад 14.37 Розв'язати рівняння
8•81^x+9•64^x=17•72^x
У відповідь записати суму коренів рівняння.
Розв'язування: Рівняння спростимо до квадратного, попередньо розділивши на 8^2х та розписавши показники

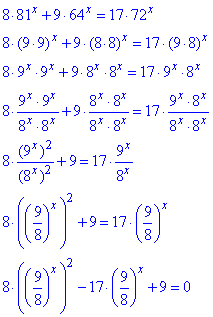
Заміна змінних: (9/8)^x=t, де t>0.

Через дискримінант обчислюємо корені рівняння 

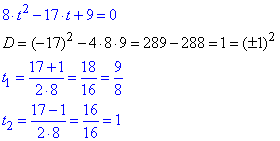
Повертаємося до заміни та розв'язуємо прості показникові рівняння

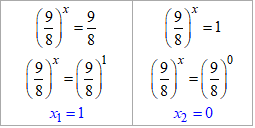
x₁+x₂=1+0=1 – шукана сума коренів.
Відповідь: 1.

Приклад 14.39 Розв'язати рівняння

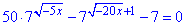
Розв'язування: В показнику рівняння маємо змінну зі знаком мінус під коренем, а це є додатковою умовою для ОДЗ: x≤0. Далі спрощуємо рівняння до квадратного

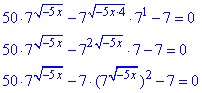
заміна: 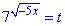, причому t>0.
Корені рівняння після заміни змінних визначаємо через дискримінант

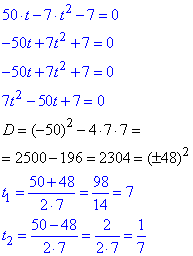
Повертаємося до заміни, прирівнюємо показники та методом піднесення до квадрату позбуваємося коренів квадратних

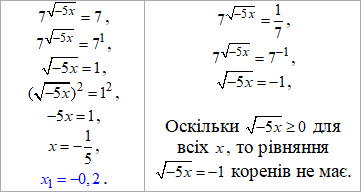
x=-0,2 -розв'язок рівняння.
Відповідь: -0,2.

Більше прикладів на різні техніки розкриття показникових рівнянь Ви можете переглянути в сусідніх статтях. Якщо маєте знайомих учнів 10, 11 класів, то можете порекомендувати їм сайт для підготовки до ЗНО тестування.