Продовжуємо вчитися обчислювати логарифмічні рівняння і сьогодні проаналізуємо кілька готових прикладів з курсу ЗНО підготовки. Завдання середні за складністю, основні формули необхідні для розв'язування будемо давати в ході пояснень.
Приклад 16.22 Установити відповідність між рівняннями (1–4) та множинами їх коренів (А–Д).
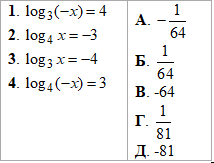
Розв'язування: Усі чотири варіанти ЗНО тестів розв'язуємо за допомогою правила:
логарифм основи рівний одиниці. Це дозволяє отримати логарифми з однаковими основами в лівій та правій частині рівняння, а далі множник перед логарифмом вносимо як степінь виразу у логарифмі:
k•logab=logabk
Цю властивість Ви часто зустрічали при спрощення логарифмічних виразів, тому повинні її знати.
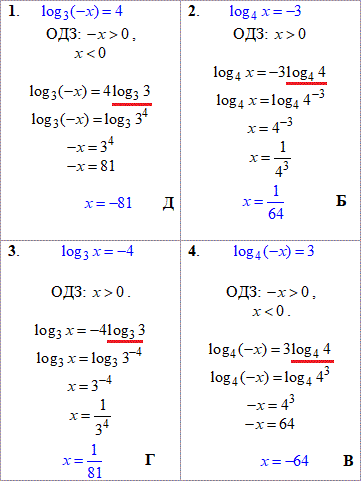
Приклад 16.26 Установити відповідність між рівняннями (1–4) та їх коренями (А–Д).
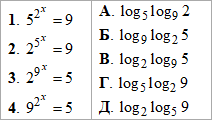
Розв'язування: Маємо 4 показникові рівняння, які методом повторного логарифмування розкриваємо.
Спрощувати допомагає знання формули, що логарифм основи рівний одиниці logaa=1.
За основу в прикладах маємо числа 2, 5, 9.


Уважно розберіть, що і чому скорочували, на ЗНО тестах таких прикладів багато.
Приклад 16.27 Розв’язати рівняння log7(x-2)-log7(x+2)=1-log7(2x-7).
Розв'язування: Під логарифмами різні функції, тому спершу випишемо нерівності для ОДЗ:
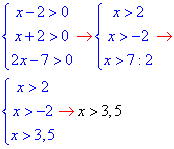
При зведенні логарифмів до спільної основи використали формулу logab-logac=loga(b/c) переходу від різниці логарифмів до логарифма частки
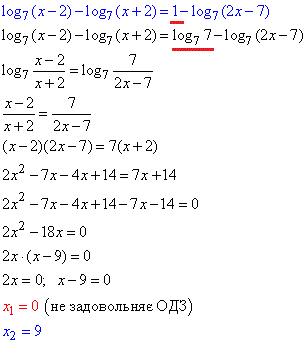
Відповідь: 9.
Приклад 16.28 Розв’язати рівняння
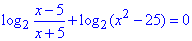
Розв'язування: Вирази під логарифмом повинні приймати додатні значення, це і є умовою на встановлення ОДЗ:
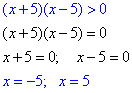
В підсумку отримали два інтервали
x∈(-∞;-5)∪(5;+∞).
За формулою logab+logac=loga(b•c) суму логарифмів виразів заміняємо логарифмом їх добутку:
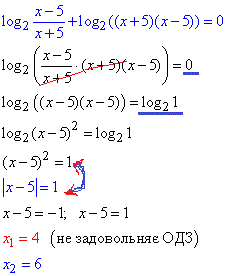
Далі при рівних основах прирівнюємо вирази під логарифмами та розписуємо їх.
Не забувайте, щоб добути вираз з під квадрату потрібно взяти його по модулю, тобто розв'язати відповідне рівняння з модулем.
Відповідь: 6.
Приклад 16.29 Розв’язати рівняння lg2(x^4)-lg(x^14)=2. У відповідь записати найменший корінь рівняння.
Розв'язування: У логарифмі маємо "ікси" в парних степенях, тому умова ОДЗ має вигляд: x≠0.
Це означає, що розв'язком логарифмічного рівняння може бути від'ємне значення.
Якщо Вас про таке питатимуть, сміло можете вказати на цей приклад.
Зводимо рівняння до квадратного
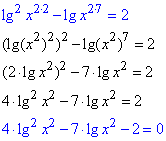
за допомогою заміни: lg(x^2)=t.
Теорема Вієта тут не допоможе, тому через дискримінант обчислюємо корені
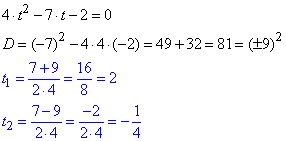
Повертаємося до заміни та обчислюємо прості р-ня з логарифмом десятковим
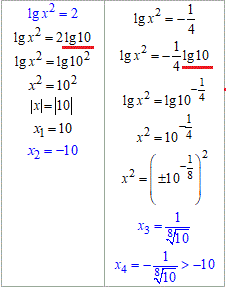
x=-10 – найменший корінь рівняння.
Відповідь: -10.
Приклад 16.30 Розв’язати рівняння 4lg(x2^2)-lg2(-x)=16. У відповідь записати x0:1000, де x0 – корінь рівняння.
Розв'язування: ОДЗ: -x>0, тобто x<0.
Маємо звідне до квадратного логарифмічне р-ня
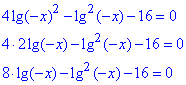
Заміна: lg(-x)=t,
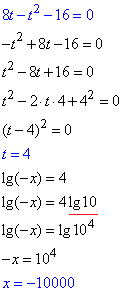
Число -10000 – корінь заданого рівняння.
Але у відповідь записуємо не сам розв'язок, а результат ділення
x0:1000=-10.
Відповідь: -10.
Приклад 16.31 Розв’язати рівняння 1/(5-lg(x))+2/(1+lg(x))=1. У відповідь записати модуль різниці коренів.
Розв'язування: Маємо дробове рівняння де в знаменнику різні вирази з логарифмами.
Розпишемо нерівності для визначення ОДЗ дробових функцій та логарифмів:
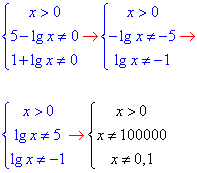
Дробове логарифмчне рівняння зводимо до квадратного
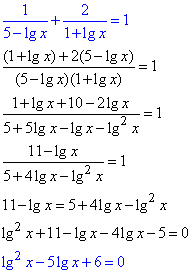
Заміна: lg(x)=t, де t≠5, t≠1 (з урахуванням ОДЗ).
t2-5t+6=0,
За теоремою Вієта
t1=2 і t2=3.
Повертаємося до заміни та розв'язуємо найпростіші логарифмічні рівняння
lg(x)=2 і lg(x)=3,
lg(x)=2lg(10) і lg(x)=3lg(10),
lg(x)=lg(102) і lg(x)=lg103,
x=10^2 і x=10^3,
x1=100 і x2=1000 – корені рівняння.
Обчислимо модуль їх різниці:
|x2-x1|=|1000-100|=900.
Відповідь: 900.
Думаю, пояснення Вам не легко далися, проте промінчик світла та надію, що колись так само легко зможете розв'язувати Ви отримали. Доброю мотивацією для багатьох учнів є необхідність проходити ЗНО тести перед вступом у ВУЗи. Дехто з Вас займається з репетитором, хто не має можливості максимально розв'язує самостійно + переглядає готові приклади в інтернеті.
Ви маєте багато шляхів досягти гарних результатів, тому не зупиняйтеся на досягнутому та кожного разу ставте перед собою більшу мету!


