Приклади з номерами за 45 на ЗНО тестах одні з найважчих. Читаючи пояснення до обчислень учні 10-11 класів можуть добре підготуватися до олімпіад чи контрольних, вивчать немало формул, та точно поглиблять знання властивостей логарифмів та вміння все це застосувати на практиці.
Приклад 16.32 Розв’язати рівняння
lg2(100^x)+lg2(10^x)=14+lg(1/x).
У відповідь записати найбільший корінь рівняння.
Розв'язування: Усі логарифми окрім lg(1/x) містять додатні вирази, тому для нього випишемо умову на ОДЗ:
1/x>0, x>0.
Зведемо рівняння до квадратного
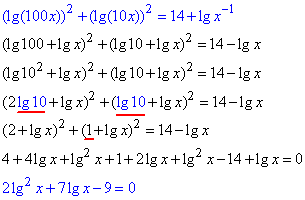
Заміна: lg(x)=t,
2t^2+7t-9=0.
Розв'язки знаходимо через дискримінант
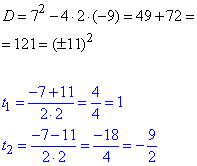
Використовуємо заміну та розв'язуємо найпростіші логарифмічні рівняння.
lg(x)=1
lg(x)=lg(10)
x1=10
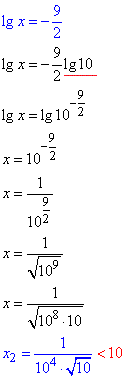
x=10 – найбільший корінь рівняння.
Відповідь: 10.
Приклад 16.33 Розв’язати рівняння
log5x+logx25=3.
У відповідь записати добуток коренів рівняння.
Розв'язування: ОДЗ: x>0, x≠1.
Спростимо звідне до квадратного логарифмічне рівняння
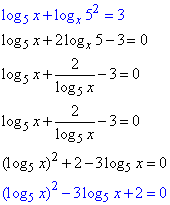
Заміна: log5x=t,
t^2-3t+2=0,
за теоремою Вієта:
t1=1 і t2=2.
Пригадуємо, що робили заміну t=log5x, підставляємо та обчислюємо логарифми:
log5x=1
log5x=log55
x1=5.
log5x=2 log5x=2log55
log5x=log55^2 x1=5^2
x2=25.
Обидва "ікси" 5, 25 є розв'язками логарифмічного рівняння, оскільки належать ОДЗ.
За умовою знайдемо добуток розв'язків:
x1•x2=5•25=125.
Відповідь: 125.
Приклад 16.34 Розв’язати рівняння
log2x•log4x•log8x=36.
Розв'язування: Маємо потрійний добуток логарифмів.
Записуємо ОДЗ: x>0.
Перетворимо вираз у лівій частині рівняння:
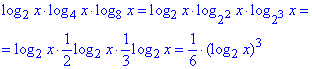
Розписуємо рівняння та, використовуючи властивість logbb=1, переходимо до спільної основи
1/6•(log2x)3=36
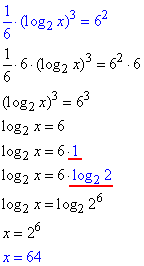
Відповідь: 64.
В онлайн курсах чи відеоуроках Ви таких прикладів не зустрінете, їх важко читати, зате багато нового вчать. І повірте, що наведені пояснення надовго Вам відкладуться в пам'яті.
Приклад 16.35 Розв’язати рівняння
x^lg(x)=1000x^2.
У відповідь записати найменший корінь рівняння.
Розв'язування: ОДЗ: x>0, x≠1.
Логарифми десяткові неоднократно спрощували, тож перетворимо рівняння до квадратного
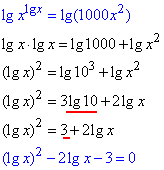
Заміна: lg(x)=t,
t^2-2t-3=0,
За теоремою Вієта:
t1=-1 і t2=3.
Повертаємося до t=lg(x) та обчислюємо:
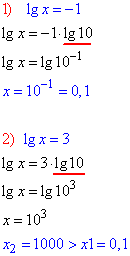
Рівняння має два корені, причому обидва належать ОДЗ.
В умові питають за найменший з коренів, тому вибираємо x=0,1 .
Відповідь: 0,1.
Приклад 16.36 Розв’язати рівняння
6^(log6x)2+x^log6x=12.
У відповідь записати добуток коренів рівняння.
Розв'язування: Переходимо до поєднання показникових рівнянь з логарифмічними.
ОДЗ: x>0, x≠1.
За допомогою основної показникової тотожності a^(logab)=b спростимо вираз 6^(log6x)2:
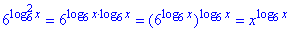
Підставимо та зведемо до логарифмів з рівними основами
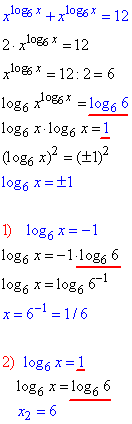
Обидва значення 6, 1/6 є розв'язками, оскільки належать ОДЗ.
Обчислимо добуток коренів:
x1•x2=6•1/6=1.
Відповідь: 1.
Приклад 16.37 Розв’язати рівняння 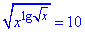 . У відповідь записати добуток коренів рівняння.
. У відповідь записати добуток коренів рівняння.
Розв'язування: Під коренем маємо змінну в степені логарифм від кореня квадратного змінної.
Хочеться спитати тих хто підбирає приклади на ЗНО тести, де можна знайти застосування таких прикладів в житті.
На мій погляд, це знущання над учнями 10-11 класів, а не перевірка знань з математики.
Але немає іншого виходу, як навчити Вас розкривати такі рівняння логарифсуванням
ОДЗ: x>0, x≠1.
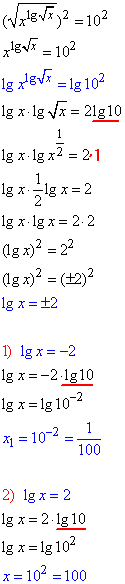
З формул бачимо, що обидва розв'язки входять в область допустимих значень.
Обчислимо їх добуток:
x1•x2=100•1/100=1.
Відповідь: 1.
Порівняйте пояснення до обчислень, формули з тим, що мали на першому уроці чи тим, що вивчаєте вшколі.
А тепер добре подумайте, перш ніж вибирати спеціальність та ВУЗ, та не помиліться!
Приклад 16.38 Розв’язати рівняння
3logx4+2log4x4+3log16x4=0.
У відповідь записати суму коренів рівняння.
Розв'язування: ОДЗ: x>0, x≠1.
Для спрощення суми логарифмів слід використати формули зміни основи в логарифмі, і навіть якщо Ви її знаєте, то це ще не гарантія, що результат перетворень у Вас вийде правильним

Можливо хтось спробує знайти оптимальнішу методику обчислень, яка веде до компактнішого запису, але в нас чомусь получилася велика формула, яка ледь на мобільні екрани вміщається.
Та є і позитив, ми звели обчислення до квадратного рівняння, а їх усі вміють розв'язувати.
Заміна: log4x=t,
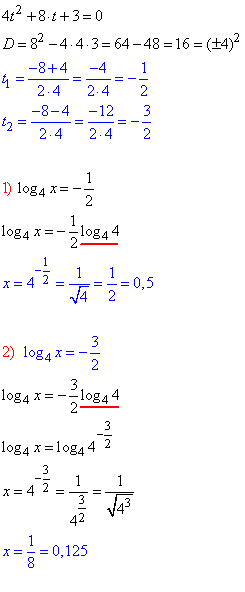
Розв'язки простих логарифмічних рівнянь належать ОДЗ.
Наостанок, обчислюємо суму:
x1+x2=0,5+0,125=0,625.
Відповідь: 0,625
Приклад 16.39 Розв’язати рівняння
|log√5x-4|-|log5x-4|=1.
У відповідь записати добуток коренів рівняння.
Розв'язування: Маємо різницю модулів від виразів з логарифмами, причому в основі √5 та 5.
Це не рівняння з параметром, але обчислень побачите не менше.
ОДЗ: x>0.
Зведемо логарифми до однієї основи
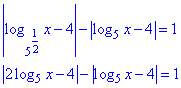
При розкритті модулів можливі три випадки, а значить додаткові три логарифмічні р-ня. Будьте уважні, коли розкриваєте модуль, слідкуйте за знаками.
Повні пояснення розберіть самостійно з таблиць.



Результатом обчислень будуть два розв'язки, що належать ОДЗ.
Обчислимо їх добуток:
x1•x2=125•0,2=25.
Відповідь: 25.
Приклад 16.40 Дано рівняння
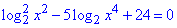
1) Указати кількість коренів рівняння;
2) знайти найбільший розв'язок рівняння.
Розв'язування: ОДЗ: x≠0.
Бачимо, що маємо р-ня звідне до квадратного, потрібно винести степені з 2 логарифма
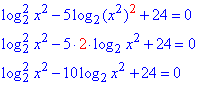
Далі заміна: log2x^2=t,
t^2-10t+24=0,
За теоремою Вієта розв'яжемо квадратне рівняння:
t1=4, t2=6.
Повертаємося до заміни t=log2x2 та за відомим алгоритмом спрощуємо логарифмічні рівняння
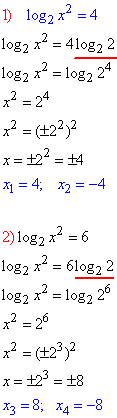
Усі 4 корені належать ОДЗ.
Підсумовуємо результати:
1) рівняння має 4 корені;
2) x=8 – найбільший корінь рівняння.
Відповідь: 1) 4; 2) 8.
На цьому курс ЗНО підготовки з обчислення логарифмічних рівнянь завершено. Удачі всім Вам на екзаменах, легких завдань на контрольних та побільше позитиву від навчання!


