Логарифмічні рівняння. Зведення до спільної основи

Основним методом розкриття логарифмічних рівнянь є зведення до спільної основи. Для цього слід використовувати рівносильні перетворення та дві чудові властивості логарифмів:

логарифм основи рівний одиниці
log_aa=1.
логарифм одиниці рівний нулю
log_a1=0.

Без цих формул ніяк не вдасться розписати логарифми та прийти до рівнянь найпростішого типу
log_af(x)=c⇔f(x)=a^c.{x>0, x≠1, f(x)>0}

Переходимо до аналізу відповідей до прикладів із ЗНО тестів. З уроку Ви в повній мірі познайометеся з рівняннями, звідними до квадратних, вивчите метод логарифмування та краще зрозумієте, для чого ми наголошуємо на вивченні наведених вище формул.

Приклад 16.16 Розв'язати рівняння lg(x)log₂x=lg(2) і знайти суму його коренів.

Розв'язування: ОДЗ: x>0.
За допомогою формули переходу до іншої основи під логарифмом

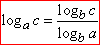
зведемо вираз log₂(x) до десяткових логарифмів (логарифмів з основою 10):
На її основі запишемо
log₂(x)=lg(x)/lg(2)
(тут a=2, b=10, c=x і log₁₀x=lg(x)).
Формули розкриття логарифмів

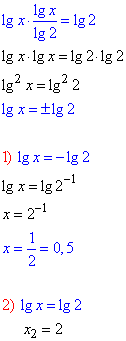
Обидва значення (0,5 і 2) належать ОДЗ, знайдемо їх суму:
x₁+x₂=0,5+2=2,5.
Відповідь: 2,5 – А.

Приклад 16.17 Розв'язати рівняння 5^log₃x+x^log₃5=50 і вказати проміжок, якому належить його корінь.

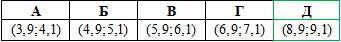
Розв'язування: ОДЗ логарифма: x>0.
Спростимо показниковий вираз 5^log₃x, помінявши попередньо за формулою log_ac=1/log_ca підлогарифмічний вираз з основою:

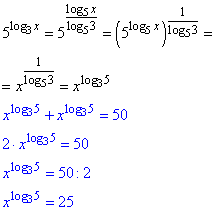
Прологарифмуємо обидві частини рівняння за основою 3:

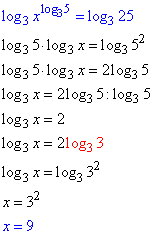
Корінь x=9 належить ОДЗ і проміжку (8,9;9,1).
Відповідь: (8,9;9,1) – Д.

Приклад 16.18 Указати рівняння, рівносильне рівнянню lgx(x+9)+lg(x+9)/x)=0.

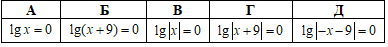
Розв'язування: ОДЗ: x(x+9)>0,
Розкриваємо нерівність методом інтервалів
x(x+9)=0,
x₁=-9, або x₂=0.

x∈(-∞;-9)∪(0;+∞).
У рівносильних рівнянь множини коренів співпадають.

Логарифм добутку та частки заміняємо сумою та різницею логарифмів

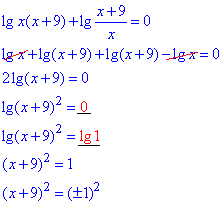
x+9=1, або x+9=-1,
x=1-9, або x=-1-9,
x₁=-8>-9, або x₂=-10.
Зауважимо x₁=-8 не належить ОДЗ (-∞;-9)∪(0;+∞), тому не є розв'язком вихідного р-ня
-9<-8<0.
Значення x=-10 – єдиний корінь рівняння.
Число x=-10 є коренем таких рівнянь:
lg|x+9|=0 і lg|-x-9|=0, але вказані рівняння також мають другий корінь:
x=-8.
Тому множини коренів обох вказаних рівнянь не співпадають із множиною коренів заданого рівняння. Звідси слідує, що кожне з них не є рівносильним заданому рівнянню.
Відповідь: таких рівнянь немає.

Приклад 16.19 Розв'язати рівняння 5^2x=7.

Розв'язування: Маємо показникове рівняння, яке розв’язуємо двократно застосовуючи метод логарифмування:

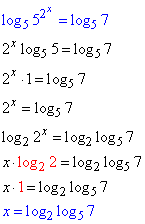
Відповідь: log₂log₅7 – Б.

Приклад 16.20 За якого найбільшого значення параметра a рівняння (x-a)log₂(3x-8)=0 має один корінь?

Розв'язування: ОДЗ функції під логарифмом:
3x-8>0; 3x>8; x>8/3.
Знайдемо розв'язки кожного з множників =0
(x-a)log₂(3x-8)=0
x-a=0, або log₂(3x-8)=0
x=a, або log₂(3x-8)=log₂1
3x-8=1
3x=1+8=9
x=9:3=3.
Якщо параметр a=3, де a>8/3, то задане рівняння матиме один корінь, а саме x=3.
Відповідь: 3 – Д.

Приклад 16.21 Установити відповідність між рівняннями (1–4) та множинами їх коренів (А–Д).

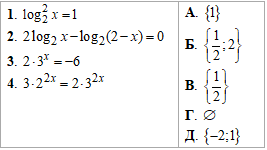
Розв'язування: Логарифмічні рівняння зводимо до спільної основи за допомогою властивостей, що логарифм основи рівний одиниці та
логарифм одиниці рівний нулю.

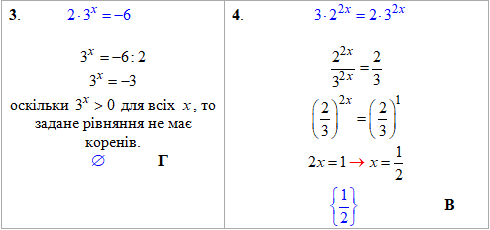
Приклад 16.23 Установити відповідність між рівняннями (1–4) та їх коренями (А–Д).

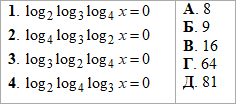
Розв'язування: Маємо потрійні вложені логарифми. Щоб їх розписати, заміняємо праву сторону за правилами (1,2) і далі при рівних основах прирівнюємо вирази у логарифмах.

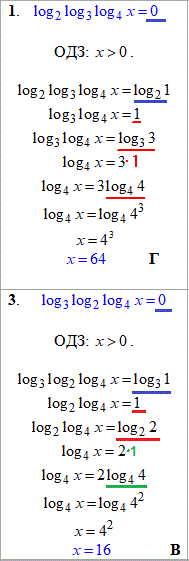
З підкреслених формул Ви бачите, наскільки важливо знати Чому дорівнює логарифм основи? =1
та Чому дорівнює логарифм одиниці? =0.
А ще краще, вміти віртуозно використовувати ці два правила при обчисленнях.

Приклад 16.25 Установити відповідність між рівняннями (1–4) та кількістю їх коренів (А–Д).

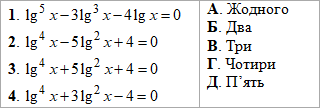
Розв'язування: Звідні до квадратних логарифмічні рівняння спрощуємо методом заміни змінних. Так як усі 4 рівняння відносно логарифма десяткового, то використовуйте властивість, що логарифм десятковий від 10 рівний одиниці.
Детальні пояснення ходу обчислень наведені в таблицях.


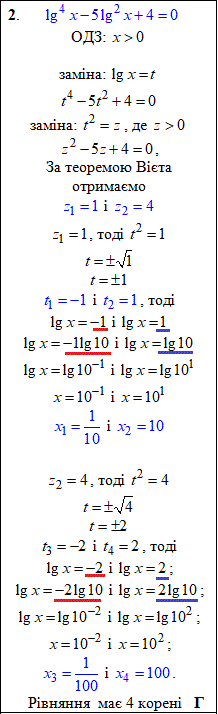
Перетворень багатсько і всі вони ґрунтуються на властивостях логарифма, тому вчіть їх, без них не знайти розв'язків складних логарифмічних рівнянь.
Дозволяємо використання матеріалів сайту вчителями при підготовці онлайн курсів, презетацій та навчальних заходів, тільки дотримуйтесь авторських прав.
(не забувайте вказувати першоджерело рисунків)