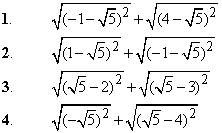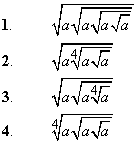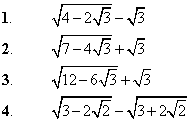Продовжуємо розбирати приклади на ірраціональні вирази, які взяли із програми підготовки до ЗНО тестування. Завдання різнотипні, це дозволяє пояснити більшість схем та методик обчислень. Все що Вам потрібно – це уважно прочитати та самостійно повторити на подібних прикладах.
Приклад 5.29 Установити відповідність між виразами (1–4) та їх значеннями (А–Д).
1. √18-√32+√72 | А. 2√2 |
Обчислення: Коли потрібно знайти суму коренів одного порядку від різних чисел то Вам потрібно розкласти числа під коренями та винести спільні для усіх. Решта множників дадуть або повні квадрати, або допоможуть спростити вираз
1)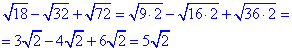 - Г.
- Г.
2) Виділяємо двійку під коренем, решта множників є квадратами чисел
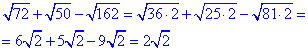 - А.
- А.
3) В цьому та наступному завданні слід також розкласти підкореневі вирази на двійку і числа, з яких легко добути корені квадратні
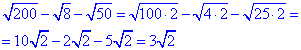 - Б.
- Б.
4) Запам'ятайте, що ніхто великих чисел Вам загадувати не буде, а під коренем слід розгледіти у більшості випадків або двійку на квадрат числа, або трійку на число в квадраті.
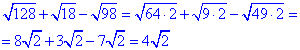 - В.
- В.
Приклад 5.30 Установити відповідність між виразами (1–4) та їх значеннями (А–Д).
| А. 1 |
Обчислення:В усіх чотирьох завданнях маємо корені квадратні з квадратів виразів, тому при розкритті отримаємо вираз за модулем.
Далі правильно розкриваємо модулі, для цього порівнюємо числа які містяться в різницях.
1) 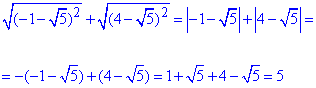 - Д.
- Д.
2) Методика не складна і все зводиться до правильного розкриття модулів, а це вже багато разів розжовано в прикладах на модулі
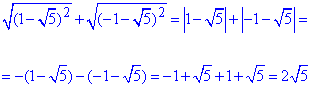 - Г.
- Г.
3) В окремих прикладах розкриття модулів в підсумку дає ірраціональний вираз, в окремих цілі числа
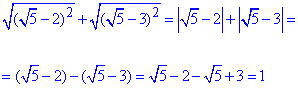 - А.
- А.
4) Як розкривати модулі надіюсь Ви знаєте, якщо ні – то даємо Вам маленьку підказку.
Число що не є під коренем підносимо до степеня кореня і порівнюємо з підкореневим числом.
В такий спосіб швидко бачимо чи при розкритті модуля потрібно міняти знак на протилежний чи залишити вираз без змін.
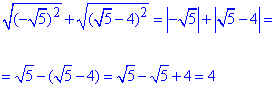 - В.
- В.
Приклад 5.31 Установити відповідність між виразами (1–4) та тотожно рівними їм степенями (А – Д).
| А. a7/16 |
Обчислення:Маємо завдання на три або чотири вложені корені. Щоб спростити записи доцільно від коренів перейти до показникової форми запису виразів. В результаті отримаємо:
1) 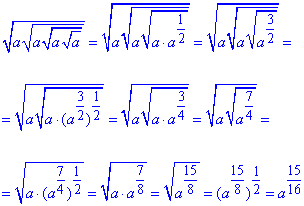 - Д.
- Д.
2) В цьому та наступних пунктах маємо по три вкладені корені. Спрощуємо кожен з прикладів, застосовуючи необхідні для цього властивості показників
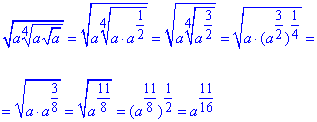 - В.
- В.
3) Як бачите нічого складного тут немає. Якщо маємо корінь квадратний то в показниковій формі отримаємо вираз в степені 1/2, для кореня кубічного матимемо вираз в степені 1/3 і так далі. А вже з показниками набагато продуктивніше можна оперувати, якщо добре вивчити їх властивості.
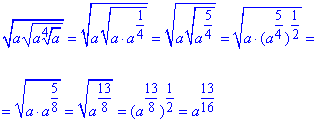 - Г.
- Г.
4) 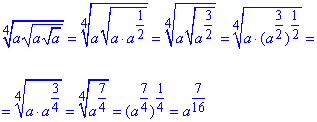 - А.
- А.
Ще раз наголошуємо, що тільки практика та самостійна робота дозволять Вам без проблем обчислювати приклади на розкриття ірраціональності.
Приклад 5.32 Установити відповідність між виразами (1–4) та їхніми значеннями (А – Д).
| А. -2 |
Обчислення: Такий тип завдань розв'язують методом виділення повного квадрата в одному з доданків.
1) 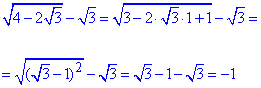 - Б.
- Б.
Якщо натренуватися на простих прикладах, то далі Вам з вигляду завдання буде зрозуміло до якого типу зводити та як розв'язувати.
2) В кожному прикладі ця процедура повторюється
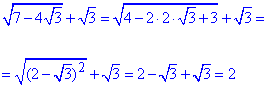 - Г.
- Г.
3) 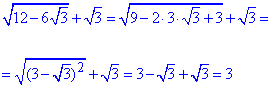 - Д.
- Д.
4) В останньому прикладі квадрат виразу виділяємо у кожному з доданків
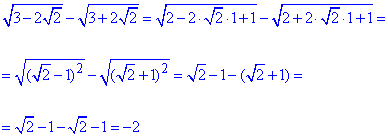 - А.
- А.
Тут не записували модулі при розкритті коренів квадратних, оскільки вирази що тут задані є додатними.
Приклад 5.33 Обчислити: 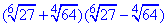
Обчислення: Маємо готовий приклад для застосування формули різниці квадратів, все решта це елементарні перетворення показників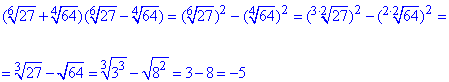
Незважаючи, що на початку мали корені 6 порядку, знання формул скороченого множення та властивостей показників дозволило спростити результат до компактного запису.
Відповідь: -5.
Приклад 5.34 Обчислити: 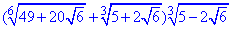 .
.
Обчислення: Перетворень в завданні чимало і всі вони пов'язані з виділенням повних квадратів, групуванням та роботі з показниками.
Самостійно розберіться з наведеною формулою, Вам це допоможе завчити методику розкриття ірраціональностей для наведеного типу прикладів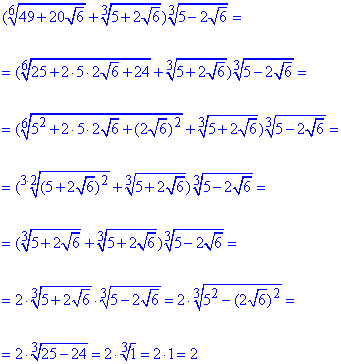
Відповідь: 2.
Коренів кубічних та старших степенів не слід боятися, правила для показників та методики, що тут даються універсальні і дозволяють оперувати будь-якими степенями. Все в чому Вам потрібно розібратися - це бачити коли потібно виділити різницю квадратів чи кубів, або квадрат виразу; правильно розкривати модулі та понижувати степінь вложеності коренів.
З практикою такі завдання Вам даватимуться все легше, але до цього треба прийти, тому самостійно обчислюйте приклади на спрощення кореневих виразів.
Далі Вас чекають ще кілька прикладів із ЗНО тестів на ірраціональні вирази, після них переходимо до розв'язування рівнянь та нерівностей з коренями.