З попереднього уроку нам залишилося проаналізувати відповіді до логарифмічних нерівностей, що містять квадратичні та дробові функції. Складність обчислення дещо зростає, але основне на що слід звертати уваги ми Вам розкажемо, коментуючи готові відповіді.
Правила як розв'язувати логарифмічні нерівності

та перейдемо до завдань з онлайн курсу ЗНО підготовки.
Приклад 22.7 Знайдіть множину розв'язків нерівності
21. Задано логарифм десятковий, основа =10>1.
Тому при опусканні логарифмів знак нерівності залишаємо без змін (1 правило)

22. Далі під логарифмом розглянемо квадратичні функції.
Такі нерівності дещо складніші, розв'язують їх методом інтервалів чи підставлення.

25. Основа логарифма менша одиниці 0,7<1, тому при переході до нерівності без логарифма знак "≤" змінюємо на протилежний "≥".
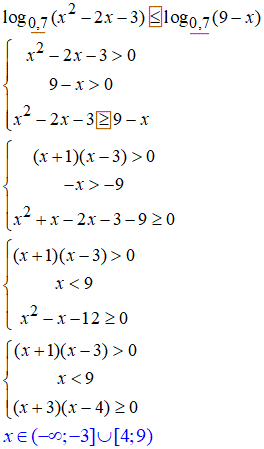
26. Зважаючи, що основа менша одиниці 1/3<1, змінюємо при переході знак нерівності на протилежний.
Якщо мали менше або рівне ≤, то після переходу отримаємо більше або рівне ≥.
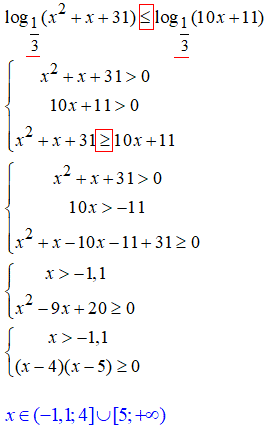
Приклад 22.11 Знайдіть множину розв'язків нерівності
27.Під логарифмом квадратична залежність, тому при обчисленнях отримаємо квадратичні нерівності.
Як їх розв'язувати простежте з формул:
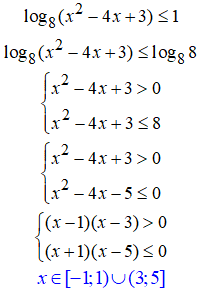
28. Основа менша одиниці 0,5<1, тому при позбутті логарифмів знак нерівності змінюємо на протилежний.
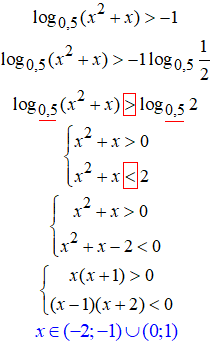
Вкінці виписуємо спільні розв'язки для системи двох нерівностей.
29. Якщо права сторона нерівності дорівнює нулю, то за властивістю логарифма її заміняємо логарифмом одиниці.
Ви маєте знати, що незалежно від того яка основа, логарифм одиниці рівний нулю.
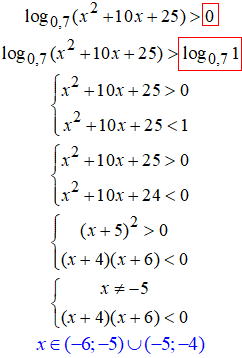
30.
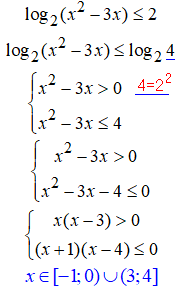
31. Далі розберемо нерівності де під логарифмом задана дробова функція.
Легко здогадатися, що вона не тільки повинна бути додатною, а й знаменник дробу не повинен дорівнювати нулю.
Не забувайте дописувати цю умову до ОДЗ логарифма.
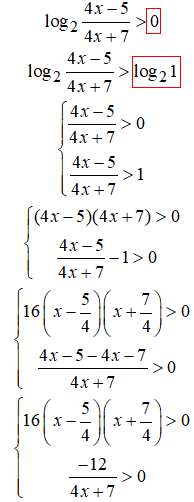
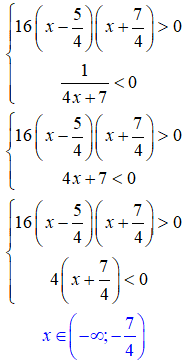
Тут багато повторень, оскільки маємо систему нерівностей і одночасно повинні задовільнятися усі нерівності.
На тестах радимо обчислювати кожну нерівність окремо, а у відповідь записувати спільні для них розв'язки.
Це зекономить час на повторення одного і того ж.
32. Тут маємо логарифм десятковий, основа =10>1.
В нерівностях можна знаменник переносити в чисельник, тільки пам'ятати, що він не перетворюється в нуль.
На знак нерівності такі перетворення не впливають, а ми ж при розрахунках, виписуємо розв'язки керуючись тільки знаками функцій на інтервалах.
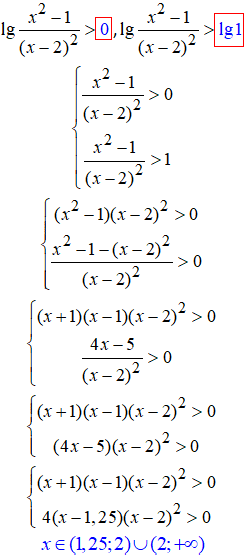
33. Уважно розберіть як перетворювати нерівності.
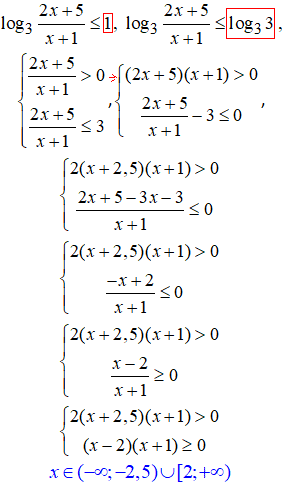
34. Маємо під логарифмом дробову функцію.
Спершу перетворюємо праву сторону нерівності, щоб отримати логарифми з однаковими основами, а далі розписуємо відповідні нерівності.
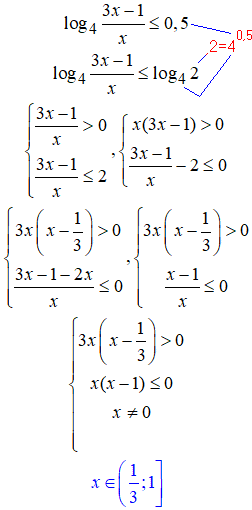
Основну масу можливих логарифмічних нерівностей ми разом розбрали. Всі перетворення базуються на кількох властивостях логарифма, тому їх потрібно вивчити і вільно вміти застосовувати. Розв'язувати систему нерівностей, як Ви могли бачити, не складно, головне бути уважними і не забувати про ОДЗ логарифма.


