На ЗНО тестах приклади на нерівності з модулями або які зводяться до квадратних нерівностей зустрічаються доволі часто, тут в додаток маємо ще й логарифми, область визначення та властивості яких потрібно врахувати. Всю простоту правила знаку при розкритті нерівності можна показати на цьому прикладі.
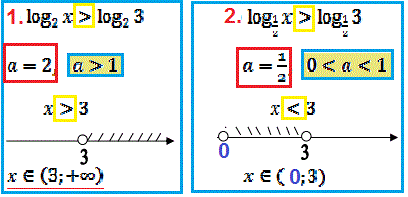
Якщо Ви його розумієте, то теоретичний матеріал за 10-11клас засвоїли на відмінно, якщо ні – повертайтеся назад на 2 уроки і перечитайте всі правила та формули, що даються для обчислень.
В курсі ЗНО підготовки маємо 50+ готових відповідей, тому легші та важчі завдання переглядайте на сусідніх сторінках сайту.
Приклад 17.21 Розв'язати нерівність
|log1/2x|≤1.
Розв'язування: Логарифмічну нерівність з модулем заміняємо системою еквівалентних нерівностей, які розкриваємо за допомогою властивості, що логарифм основи рівний одиниці 1=logaa.
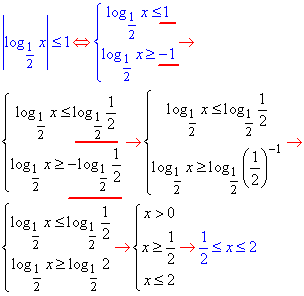
Основа 1/2<1, тому знак нерівності при опусканні логарифмів змінюємо на протилежний.
На числовій осі заштриховуємо множину розв'язків нерівності
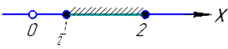
x∈[1/2;2].
Відповідь: [1/2;2] – А.
Приклад 17.22 Знайти розв'язки нерівності |log3x|≥1.
Розв'язування: За аналогічною з попереднім прикладом методикою проводимо розкриття логарифмічної нерівності
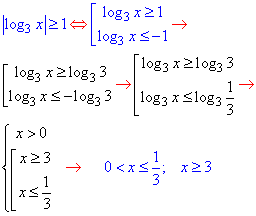
Не забувайте враховувати ОДЗ логарифма x>0:

Розв'язок x∈(0;1/3]∪(3;+∞].
Відповідь: (0;1/3]∪(3;+∞] – Г.
Приклад 17.12 Розв'язати нерівність
 .
.

Розв'язування: Маємо логарифмічну нерівність, звідну до квадратної заміною log3x=t.
Для розкриття t2-3·t+2≤0 розглянемо квадратне рівняння
t2-3·t+2=0.
За формулами Вієта:
t1+t2=3 – сума коренів;
t1•t2=2 – їх добуток.
t1=1 і t2=2 – корені квадратного р-ня.
Через прості множники записуємо
(t-1)(t-2)≤0.
Методом інтервалів розв'язуємо її.
Далі повертаємося до заміни та розкриваємо нерівності з логарифмом
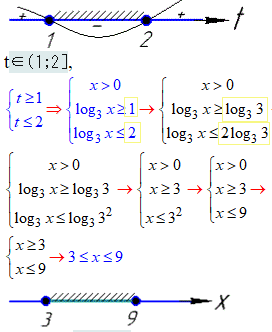
Розв'язок x∈[3;9].
Відповідь: [3;9] – В.
Приклад 17.13 Знайти розв'язки нерівності
lg2(x)+4lg(x)+3≥0.
Розв'язування: Маємо нерівність з логарифмом, звідну до квадратної
Заміна lg(x)=t.
t2+4t+3≥0,
Відповідне нерівності квадратне рівняння
t2+4t+3=0
розв'яжемо за формулами Вієта:
t1+t2=4;
t1•t2=3.
t1=1; t2=3 – корені рівняння.
Методом інтервалів знайдемо розв'язки нерівності
(t-1)(t-3)≥0.
0<x≤10 і x≥1000.
Далі повертаємося до заміни та розписуємо прості логарифмічні нерівності
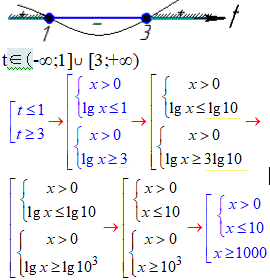

Розв'язок
x∈(0-∞;10]∪[1000;+∞).
Відповідь: (0-∞;10]∪[1000;+∞) – Д.
Приклад 17.29 Обчислити множину розв'язків нерівності
log1/2(x2-5x+6)>-1.
У відповідь записати найменше натуральне число, яке не є розв'язком нерівності.
Розв'язування: Праву сторону перетворимо за формулою
logaa=1.
Основа менша одиниці, тому не забуваємо поміняти знак при розкритті логарифма.
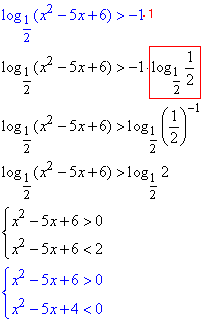
Кінцеві квадратичні нерівності обчислюємо методом нтервалів:
1) x2-5x+6=0,
за теоремою Вієта
x1=2,
x2=3.
2) x2-5x+4=0,
x3=1,
x4=4.
Наносимо множини розв'язків на числові осі
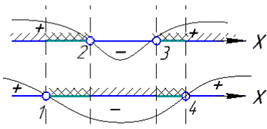
та об'єднуємо спільні x∈(1;2)∪(3;4), тобто перетин двох множин.
Зауважте, що потрібно шукати перетин розв'язків нерівностей, а не усі що знайшли.
1 - найменше натуральне число, яке не є розв'язком нерівності.
Відповідь: 1.
Приклад 17.33 Знайти множину розв'язків нерівності
lg2(100x)-5lg(x)>6.
У відповідь записати кількість натуральних чисел, які не є розв'язками нерівності.
Розв'язування: Спростимо вираз lg2(100x):
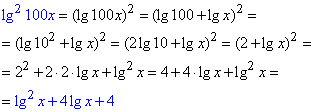
Зведемо отриману нерівність до квадратної
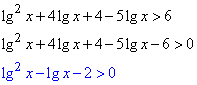
шляхом заміни змінних:
lg(x)=t, тоді
t2-t-2>0.
Відповідне квадратне рівняння
t2-t-2=0,
за теоремою Вієта:
t1=-1; t2=2.

t∈(-∞;-1)∪(2;+∞).
Повернемося до логарифмів:
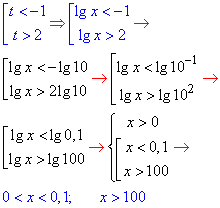

звідси x∈(0;0,1)∪(100;+∞).
Перші 100 натуральних чисел не є розв'язками нерівності.
Значення 100 також не входить, оскільки нерівність строга.
Відповідь: 100.
Приклад 17.39 Розв'язати нерівність log1/2|x|≥|x|-1.
У відповідь записати добуток усіх цілих розв'язків нерівності.
Розв'язування: Нехай маємо дві функції:
f(x)=log1/2|x| і g(x)=|x|-1.
На координатній площині побудуємо їх графіки:
f(x)=log1/2|x| – логарифмічна крива, яка утворена з графіка функції y=log1/2x відображенням симетрії відносно осі ординат (осі Oy).
ОДЗ: x≠0.
g(x)=|x|-1 – два промені, які перетинаються у точці (0;-1) і напрямлені вгору. Графік утворимо з функції y=x відображенням симетрії відносно осі ординат (осі Oy), а також з графіка функції y1=|x| зсуненням на 1 одиницю вниз.
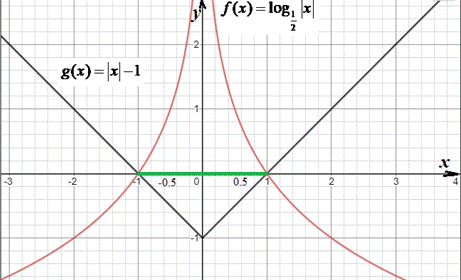
Випишемо такі значення x, при яких графік функції f(x)=log1/2|x| знаходиться вище, або перетинається з графіком функції g(x)=|x|-1
x∈[-1;0)∪(0;1].
Випишемо усі цілі розв'язки та знайдемо їх добуток:
-1 і 1, тоді -1•1=-1.
Відповідь: -1.
Приклад 17.41 Розв'язати нерівність logx+1|x-2|≤1. У відповідь записати суму всіх натуральних чисел, які не є розв'язками нерівності.
Розв'язування: За формулою logaa=1 перетворимо праву сторону
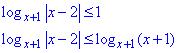
та розкриємо логарифмічну нерівнівсть з модулем, для двох варіантів основ:
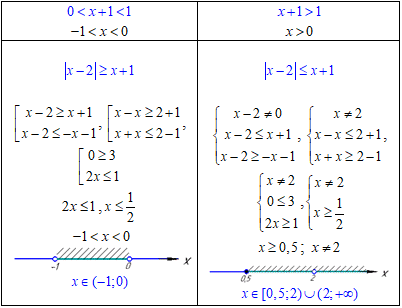
Об'єднавши розв'язки x∈(-1;0) і x∈[0,5;2)∪(2;+∞], отримаємо
x∈(-1;0)∪[0,5;2)∪(2;+∞].
Єдине натуральне число 2 не є розв'язком нерівності.
Відповідь: 2.
Попереду Вас чекають ще 2 статті з готовими прикладами на розкриття нерівностей з логарифмами.


