Перш ніж приступати до обчислень пригадаємо правила за якими розв'язують логарифмічні нерівності

Думаю Ви швидко зможете запам'ятати наведену таблицю.
Умови f(x)>0, g(x)>0 це обмеження на область допустимих значень логарифма, а простішими словами - це умова, що логарифм приймає значення більші від нуля. Далі розглянемо всеможливі нерівності, які Ви повинні навчитися розв'язувати в 10-11 класі та можуть чекати Вас при проходженні ЗНО та ДПА.
Приклад 22.1 Розв'яжіть нерівність:
1,2. В першому прикладі основа 0,1<1, тому при опусканні логарифма знак нерівності змінюємо на протилежний.
В другому прикладі знак не поміняли, оскільки основа більша одиниці 11>1.
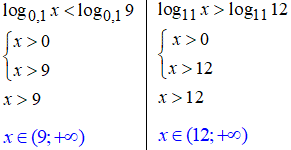
Відповідь записуємо нерівністю та у вигляді інтервалу розв'язків.
3,4. Поки, що вчимося перших двох правил з таблиці на початку уроку.
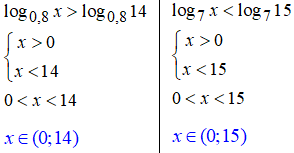
5,6. Правило зміни знаку, коли основа менша одиниці не таке і важке.
Поки що все зводиться до системи із двох нерівностей:
перша з умови, що під логарифмом додатне число;
друга - результат розкриття логарифмічної нерівності.
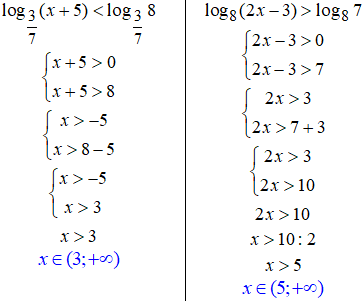
7,8. Запис "lg" означає, що маємо логарифм десятковий, тобто логарифм з основою рівною 10.
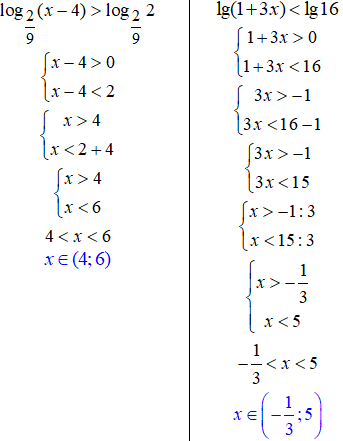
Якщо маємо "ln", то це логарифм натуральний або логарифм за основою експоненти
e≈2,718281828.
Приклад 22.3 Розв'яжіть нерівність
9, 10. Починаємо вивчення останніх двох правил розкриття нерівностей з логарифмом, коли права сторона містить не логарифм, а число.
В цьому випадку можете або використати правило або далі погляньте, як можна використати властивість, що логарифм основи рівний одиниці.
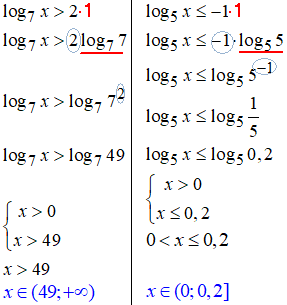
11, 12.
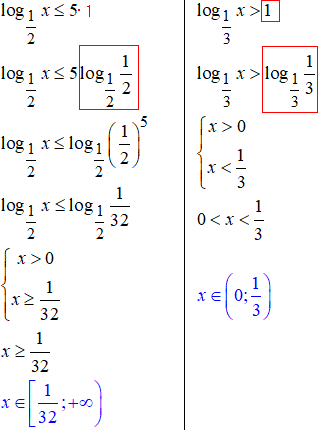
13, 14.
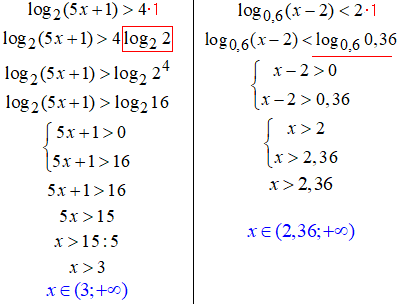
15, 16. Якщо нерівність нестрога (≤,≥), то всі Ви маєте добре знати, що і при позбутті логарифма нерівність буде нестрога.
А от ОДЗ логарифма завжди породжує строгу нерівність, тому що функція під логарифмом повинна приймати значення більші нуля.
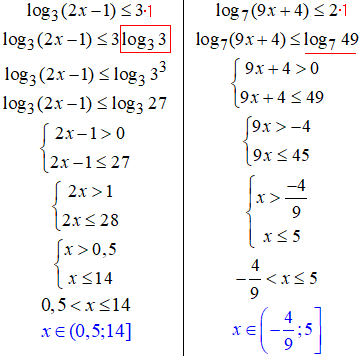
17, 18.
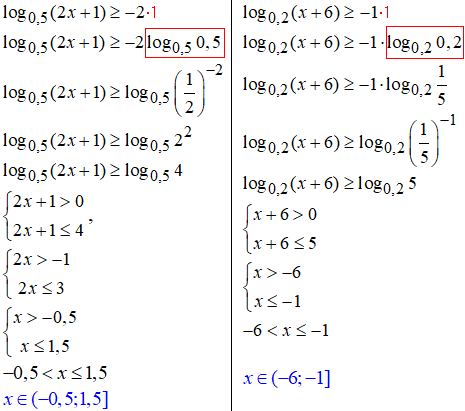
Приклад 22.5 Скільки цілих розв'язків має нерівність:
19. Перетворюємо праву сторону нерівності та розписуємо:
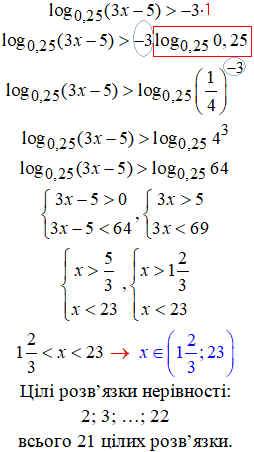
Якщо у відповідь отримали великий діапазон цілих чисел, то щоб знайти їх кількість потрібно від правого значення відняти ліве і додати 1.
Тому тут отримали такий результат
n=22-2+1=21.
20. Аналогічно поступають, якщо маємо перехід через 0 і від'ємні цілі розв'язки.
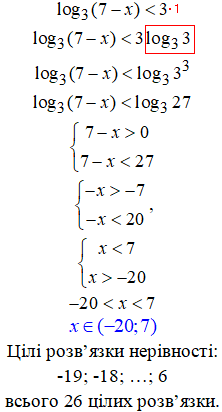
По аналогії з попереднім завданням знаходимо кількість цілих розв'язків нерівності:
n=6-(-19)+1=26.
Решту 14 прикладів розберемо на наступному уроці.


