На сьогодні на сайті розміщено понад 400 відповідей до завдань з посібника для підготовки до ЗНО, які дозволяють швидко наверстати пропущений або призабутий матеріал.
В цьому розділі наведемо пояснення до 35 прикладів з розв'язками раціональних рівнянь.
Незважаючи на те, що збірник прикладів за 2010 рік, завдання досі залишаються актуальними при підготовці до тестів, екзаменів, вступних іспитів.
Ви можете безкоштовно завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Зміст: Посібник містить поради щодо проходження ЗНО з математики, базові формули та означення та подібні до тестових завдання.
Усі задачі однієї теми розміщені в порядку зростання складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.
Тема 8. Цілі раціональні рівняння
Приклад 8.1 Розв'язати рівняння ax+b=c, де а приймає довільне відмінне від нуля значення.
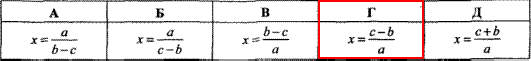
Обчислення: Перетворимо лінійне рівняння та знайдемо "ікс"
ax=c-b, x=(c-b)/a.
Відповідь: x=(c-b)/a – Г.
На елементарних завданнях довго затримуватися не будемо, більш детально зупинимося на важчих прикладах в яких потрібно скласти рівняння за умовою, розв'язати квадратне чи модульне рівняння.
Приклад 8.2 Розв'язати рівняння x/7-2=0 і -0,2x=4 та записати добуток їх коренів.

Обчислення: Знайдемо розв'язки лінійних рівнянь
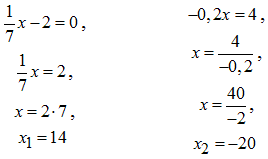
Обчислимо добуток знайдених коренів x1=14 і x2=4/(-0,2)=-20:
x1•x2=14•(-20)=-280.
Відповідь: -280 – Д.
Приклад 8.3 Розв'язати рівняння |x-1|=3 та знайти суму його коренів.

Обчислення: Рівняння з модулем розділимо на 2:
перше має місце коли підмодульна функція x-1 додатна, друге - коли від'ємна, тобто x<1.
Обчислення рівнянь подано у формулі
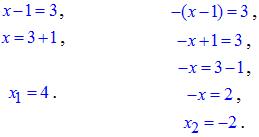
Знайдемо суму визначених коренів x1=4 і x2=-2:
x1+x2=4-2=2.
Відповідь: 2 – В.
Приклад 8.4 Знайти дискримінант рівняння 3x^2-2x-5=0.
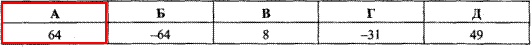
Обчислення: У рівнянні ax^2+bx+c=0 коефіцієнти при квадратничній формі рівні:
a=3, b=-2 і c=-5.
Дискримінант квадратного рівняння знаходимо за формулою
D=b^2-4ac=(-2)^2-4•3•(-5)=4+60=64.
Відповідь: 64 – А.
Приклад 8.5 Знайти суму коренів рівняння 2x^2-5x-7=0.
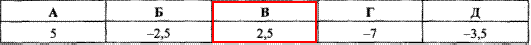
Обчислення: Поділимо усі члени рівняння на двійку:
x^2-2,5x-3,5=0
Для знаходження коренів зведеного квадратного рівняння скористаємось теоремою Вієта:
x1+x2=-b, тобто x1+x2=-(-2,5)=2,5.
Відповідь: 2,5 – В.
Приклад 8.6 Скласти зведене квадратне рівняння з коренями √2 і √8.

Обчислення: Маємо два ірраціональні корені x1=√2 і x2=√8.
Знайдемо коефіцієнти зведеного квадратного рівняння:
ax^2+bx+c=0.
Скористаємось теоремою Вієта:
x1+x2=-b, x1•x2=c.
За формулами знаходимо b, c:
x1+x2=√2+√8=√2+2√2=3√2;
x1•x2=√2•√8==√16=4.
Таким чином, a=1, b=- 3√2 і c=4, а зведене квадратне рівняння має вигляд:
x^2-3√2x+4=0.
Відповідь: 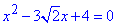 – Г.
– Г.
Приклад 8.7 Знайти суму цілих чисел, що належать відрізку, кінцями якого є корені квадратного рівняння 10x^2+7x-12=0.
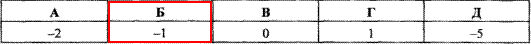
Обчислення: Розв'яжемо задане квадратне рівняння:
10x^2+7x-12=0.
Випишемо коефіцієнти a=10, b=7 і c=-12.
Спершу знаходимо дискримінант рівняння, а далі його корені
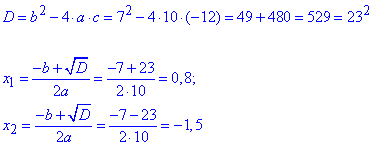
На основі розв'язку, отримали такий відрізок [-1,5;0,8].
Відрізку належать два цілих числа: 0 і -1.
Їх сума рівна 0-1=-1.
Відповідь: -1 – Б.
Приклад 8.8 Скільки коренів має рівняння |x^2-3x+2|=2?
Обчислення: Під модулем маємо квадратичну залежність, тому в залежності від її знаку при розкритті модулів отримаємо два квадратні рівняння, обчислення яких наведено у таблиці.
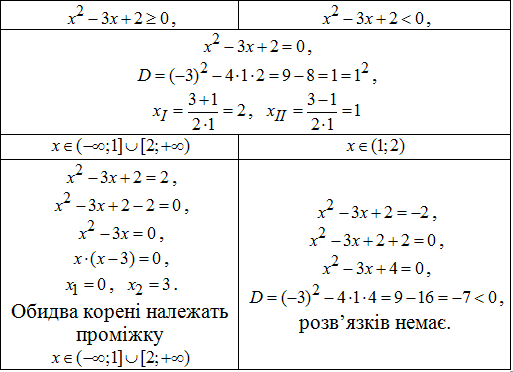
Звідси слідує, що вихідне модульне квадратне рівняння |x^2-3x+2|=2 має всього два корені.
Відповідь: два – Б.
Решта готових відповідей на раціональні рівняння пояснять, як обчислювати рівняння з параметром, шукати корені квадратних та біквадратних рівнянь, правильно складати залежності за умовою.



