З цієї статті Ви пригадаєте, а можливо і вивчите властивості показникових та логарифмічних функцій та їх застосування при спрощенні виразів. Для цього розберемо готові розв'язки ЗНО тестів до 48 завдань, які загалом містять понад 80 різних за схемою обчислень прикладів.
Щоб легше уявити про що піде мова, приведемо графік логарифмічної та показникової функції
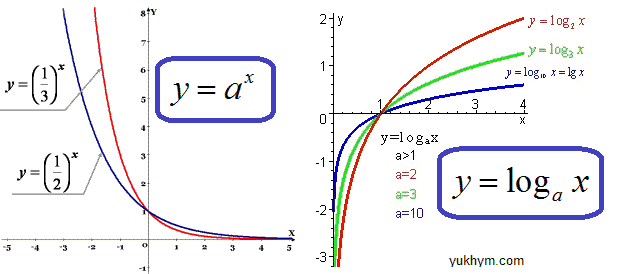
Властивості показникових залежностей та логарифмів описані в окремих статтях на сайті, тут піде мова лише про властивості функцій, які потрібно знати для спрощення виразів.
Правила та дї зі степенями
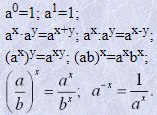
Дії над логарифмами
Означення логарифма
1. logab=c, то b=ac
логарифм основи рівний одиниці
logaa=1.
логарифм одиниці рівний нулю
loga1=0
сума логарифмів
logab+logac=loga(b·c).
формула різниці логарифмів
logab-logac=loga(b/c).
Наведені співвідношення суми та різниці логарифмів можна застосовувати як зліва направо, так і навпаки. Тобто з логарифма добутку чисел або його частки можна отримати суму або різницю логарифмів.
Правило переходу до іншої основи під логарифмом
logab=logсb/logсa.
Винесення степені з під основи логарифма та самого логарифма виконуємо за правилом:
loga^kb^p=logab
1/k·logab=loga^kb
log(a^N)=N·log(a).
І не забувайте, що є ще дві форми запису логарифму – це десятковий логарифм lg=lg10 та логарифм натуральний ln=loge – в основі експонента.
Знаком ^ позначено степінь. Умови багатьох вправ виписані в текстовій формі для швидкого знаходження завдань в пошуку сайте та загалом в інтернеті.
Спрощення показникових та логарифмічних виразів
Найпростіші приклади, які ви можете зустріти мають вигляд:
log 24=log22^2=2•log22=2•1=2;
5^log 53=3.
Методика обчислень досить проста і тому таких завдань тут буде мало.
Приклад 6.1 Вказати неправильну рівність.
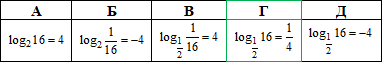
Розв'язування: В цьому завданні використаємо формули винесення показника з основи логарифма та його самого:
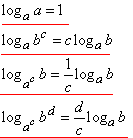
Слід перевіряти, щоб виконувалися умови a>0, a≠1, b>0, c≠0.
Розписуємо логарифми та співставляємо з правими сторонами за знаком рівності в таблиці.
log216=log224=4•log22=4•1=4 - вірно,
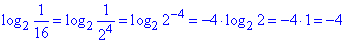 - вірно,
- вірно,
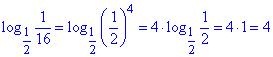 - вірно
- вірно
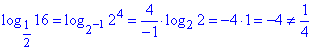 - неправильна рівність
- неправильна рівність 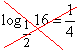 .
.
Все на цьому перевірку на ЗНО тестах можна закінчувати та записувати правильну відповідь Г.
Наша ж мета навчити Вас спрощувати логарифми, тому розв'яжемо останній варіант.
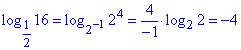 - вірно.
- вірно.
Відповідь: 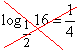 – Г.
– Г.
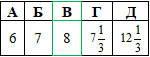
Приклад 6.2 Обчислити: 5^log57+log1/31/3+log71.
Розв'язування: Для обчислення виразу застосуємо основну логарифмічна тотожність 
яка говорить, що число a в степені логарифма за основою a від числа b>0 рівне числу b, де a>0, a≠1, b>0.
Останні обмеження слідують з ОДЗ логарифма.
Третій доданок суми визначаємо з умови, що логарифм одиниці рівний нулю
loga1=0.
Запам'ятайте ці дві формули, вони часто необхідні в розрахунках.
Знаючи все викладене вище, можемо спростити вираз
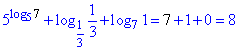
Отримали варіант В ЗНО тестів.
Відповідь: 8 – В.
Приклад 6.3 Спростити вираз (3·lg2+3·lg5)/(lg1300-lg0,13).
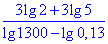
А | Б | В | Г | Д |
0,6 | 0,7 | 0,65 | 0,75 | 0,5 |
Розв'язування: Пам'ятайте, що під "lg" розуміють логарифм десятковий або логарифм за основою десять.
В цьому завданні вивчимо кілька базових властивостей логарифмів:
перше правило говорить, що сума логарифмів чисел рівна логарифму добутку чисел; друге правило, що різниця логарифмів чисел рівна логарифму частки чисел.
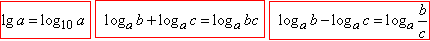
де a>0, a≠1, b>0, c>0.
Враховуючи ці та попередні формули, розпишемо вираз
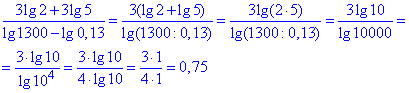
Відповідь: 0,75 – Г.
Приклад 6.4 Спростити вираз lg25/lg5=...
А | Б | В | Г | Д |
lg5 | 5 | lg20 | 2 | 0,5 |
Розв'язування: Щоб спростити частку логарифмів з однаковими основами Вам потрібно знати формулу переходу до іншої основи під логарифмом

де a>0, a≠1, b>0, c>0.
Зауважимо, що в завданні маємо десятковий логарифм "lg" з основою = 10, тому при зміні основи далі не слід писати lg.
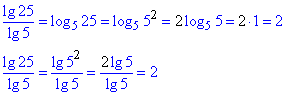
Перетворення прості.
Відповідь: 2 – Г.
Приклад 6.5 Знайти
(log8128-log82)/(log236-log29)
А | Б | В | Г | Д |
1 | 14/3 | 2 | 16 | 3 |
Розв'язування: На основі вивчених властивостей логарифма, розписуємо дріб
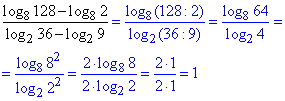
Відповідь: 1 – А.
Приклад 6.6 Обчислити
log549+2·log5(5/7)=…
А | Б | В | Г | Д |
2 | 1 | 0 | 4 | 25 |
Розв'язування: Ряд завдань на тестах складені так, що потрібно переходити від логарифма частки чисел до різниці логарифмів чисел
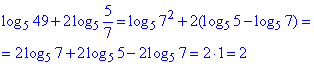
Будьте до цього готові та запам'ятайте алгоритм обчислень.
Відповідь: 2 – А.
Приклад 6.7 Знайти значення x, якщо log7x=2log76-log712+log715.
А | Б | В | Г | Д |
39 | 7,5 | 15 | 17/4 | 45 |
Розв'язування: Спростимо вираз 2log76-log712+log715 в правій частині логарифмічного рівняння:
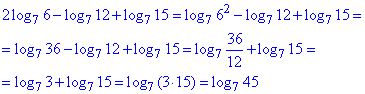
Отримали рівняння log7x=log745 в якому логарифми мають однакову основу, тому прирівнюємо внутрішні значення
x=45.
Відповідь: 45 – Д.
Приклад 6.8 Обчислити: log332/log32+log727/log73.
А | Б | В | Г | Д |
15 | 8 | 25 | 54 | 64 |
Розв'язування: Розпишемо логарифми в чисельниках дробів, записавши 32 та 27 в показниковій формі 2 та 3 відповідно
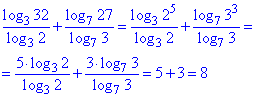
Відповідь: 8 – Б.
Приклад 6.9 Знайти значення виразу:
8^log23+9^log34.
А | Б | В | Г | Д |
33 | 7 | 14 | 43 | 60 |
Розв'язування: Потрібно записати 8 та 9 через 2^3 та 3^2, щоб застосувати основну логарифмічну тотожність
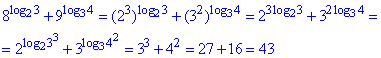
Далі використовуємо властивість, що множник перед логарифмом можна внести в логарифм і він є степенем числа (виразу) в логарифмі.
Відповідь: 43 – Г.
Приклад 6.10 Обчислити: log816.
А | Б | В | Г | Д |
8 | 2 | 3/4 | 12 | 4/3 |
Розв'язування: Подібних завдань Ви на практиці зустрінете багато, тож запам'ятайте, що степінь числа під логарифмом можна винести за логарифм і він буде множником, тоді як степінь основи виносять з логарифма як обернений множник, тобто 1 поділити на степінь основи, а далі сам логарифм
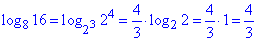
Відповідь: 4/3 – Д.
Приклад 6.11 Знайти log3200, якщо log32=a, log35=b.
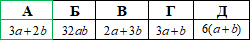
Розв'язування: Логарифми від 2 та 5, що позначені через a та b в такого типу завданнях дають підказку, що число 200 потрібно розписати як добуток множників кратних 2 та 5. Після цього логарифм добутку чисел заміняємо сумою логарифмів, та розписуємо останні
log3200=log3(8•25)=log38+log325=
=log323+log352=3•log32+2•log35=3a+2b.
Запам'ятайте наведену схему розрахунків, адже попереду ще багато прикладів, які можна розв'язати в такий спосіб + це не важкий підхід. Попереду куди важчі в плані обчислень завдання.
Відповідь: 3a+2b – А.
Приклад 6.12 Обчислити:
lg(tg10)·lg(tg20)·lg(tg30)·…·lg(tg880)·lg(tg890).
А | Б | В | Г | Д |
89 | 0,1 | 10 | 1 | 0 |
Розв'язування: Маємо добуток логарифмів тангенсів від одного градуса до 890, його б ніхто не знайшов якби не одне "но".
Тангенс 45 градусів рівний одиниці, а логарифм одиниці рівний нулю.

Запам'ятайте цей підхід, адже на його основі є багато логарифмів від тригонометричних функцій і перший приклад наступної статті є підтвердженням цьому.
Відповідь: 0 – Д.
Попереду біля 40 готових розв'язків на обчислення значення логарифмів та виразів, які в степені містять логарифм.
Діліться посиланням на відповіді та гарної вам онлайн підготовки із ЗНО тестування з математики.


