Продовжуємо розбирати відповіді до онлайн кусу із ЗНО підготовки на обчислення показникових та логарифмічних виразів. Пояснення попередніх 12 завдань познайомили Вас з багатьма властивостями показникових функцій та логарифмів, тому не зупиняйтеся та розбирайте приведені далі завдання самостійно.
Приклад 6.14 Обчислити:
7^log23-3^log27.
А | Б | В | Г | Д |
0 | 7/3 | 1 | -1 | 2 |
Розв'язування: Такого типу завдання обчислюють за допомогою формул переходу від однієї основи до іншої та заміни основи на вираз під логарифмом

де a>0, a≠1, b>0,b≠1, c>0, c≠1.
Прикладів небагато, але самі розумієте, без формули така "пісня", яка іде далі не вийде.
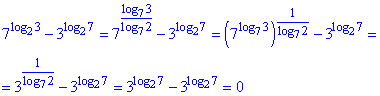 .
.
Відповідь: 0 – А.
Приклад 6.13 Обчислити:
lg(tg10)+lg(tg20)+lg(tg30)+…+lg(tg880)+lg(tg890).
А | Б | В | Г | Д |
10 | 1 | 0 | 0,1 | 89! |
Розв'язування: В попередній статті закінчили розглядом завданням на добуток логарифмів від тангенсів кутів, тут маємо суму і зовсім другу схему обчислень. Суму логарифмів від тангенсів кутів від 1 до 89 слід звести до одного логарифма від добутку тангенсів.
Після цього, враховуючи періодичність тангенса, пів ряду множників від 46 градусів і далі розписати:
tg(π/2-a)=ctg(a).
В результаті під логарифмом дістанемо попарні множники тангенса на котангенс, які за відомою тригонометричною формулою рівні одиниці.
tg(a)•ctg(a)=1.
Ну а логарифм одиниці завжди 0, тому дістанемо
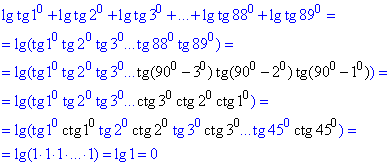
Відповідь: 0 – В.
Приклад 6.15 Обчислити: log57•log49125.
А | Б | В | Г | Д |
1/6 | 1 | 6 | 2/3 | 1,5 |
Розв'язування: Для спрощення добутку логарифмів використаємо ряд властивостей логарифма, включаючи наведені в попередньому завданні
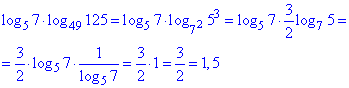
Відповідь: 1,5 – Д.
Приклад 6.16 Записати числа 2^15, 4^10, 10^5 у порядку зростання.
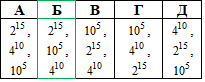
Розв'язування: Скористаємося властивістю показникових функцій
abc=(ab)c, де a>0.
Розкладаємо степінь так, щоб для всіх трьох чисел він містив спільний кратний =5. Далі його залишаємо, а числа підносимо до знайдених при 5 множників-степенів.
2^15=2^(3•5)=(2^3)^5=8^5,
4^10=(4^2•5)=(4^2)^5=16^5>10^5>8^5.
Показники у всіх чисел рівні, тож можемо порівняти задані числа і розставити у порядку зростання:
215, 105, 410.
Відповідь: 215, 105, 410 – Б.
Приклад 6.17 Спростити вираз 7^(1+log72)=…
А | Б | В | Г | Д |
9 | 14 | 49 | 343 | 81 |
Розв'язування: Є дві схеми обчислення завдань і обидві дають правильний результат, вибирайте яка Вам зручна. Перша ґрунтується на властивості показників

Другий спосіб розв'язання слідує з властивостей логарифма
7^(1+log72)=7^(log77+log72)=7^log77·2=7·2=14.
Відповідь: 14 – Б.
Приклад 6.18 Обчислити
log7+4√3(7-4√3)
А | Б | В | Г | Д |
14 | 2 | 1 | -1 | -2 |
Розв'язування: Такого типу логарифми складно спрощувати, якщо не знати як їх для Вас старанно виписують.
Тому перегляньте методику обчислень:
спершу за формулою різниці квадратів перепишемо вираз 7-4√3:
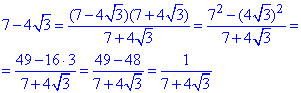
Бачимо, що в результаті отримали вираз, який обернено пропорційний основі логарифма, або його можемо записати як основа в (-1) степені.
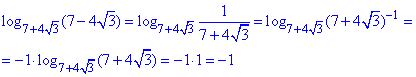
Придумайте самостійно завдання, виходячи із розглянутої схеми обчислень.
Відповідь: -1 – Г.
Приклад 6.19 Обчислити 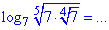
Розв'язування: Хоч в умові маємо логарифм, проте завдання на знання властивостей показників.
Спочатку спростимо вложені корені:
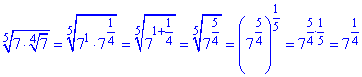
Тоді степінь сімки 7 під логарифмом виносимо, а сам логарифм основи рівний одиниці log77=1.
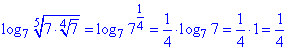
Не лякайтеся подібних завдань, вони не важкі в плані обчислень.
Відповідь: 1/4 – В.
Приклад 6.20 Знайти: log87•log76•log64=...
А | Б | В | Г | Д |
3/2 | 2/3 | 1/2 | 2 | 3 |
Розв'язування: Перше, що слід зауважити, що під логарифмами маємо різні основи, тому щоб після обчислень отримати число, необхідно застосувати формули переходу до іншої основи

У другому та третьому логарифмі перейдемо від основ 7,6 до основи рівної 8.
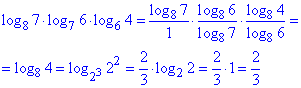
Вчіть властивості логарифма з готових прикладів, їх в час інформатизації в інтернеті багато.
Відповідь: 2/3 – Б.
Приклад 6.21 Обчислити:
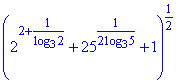
А | Б | В | Г | Д |
8 | 16 | 3 | 4 | 5 |
Розв'язування: Починаючи з цього номера в ЗНО тестах йдуть завдання в яких одночасно потрібно використовувати властивості логарифмічних та показникових функцій. Основні правила Ви знаєте, так що уважно читайте формули, оскільки схема обчисленьповторюється від завдання до завдання
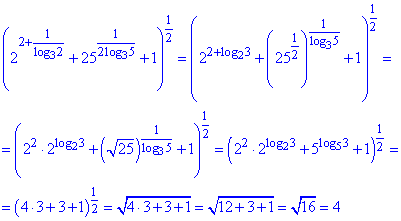
Тут найчастіше доводилося міняти місцями основу з числом під логарифмом.
Відповідь: 4 – Г.
Стаття вмістила багато нових для Вас методик обчислень та є досить об'ємною, щоб далі її продовжувати, тому решта 25 прикладів Ви б точно не переглянули.
Завдання зі складнішими умовами та готовими відповідями розберемо на наступному уроці.


