Ірраціональні рівняння. ЗНО підготовка

Продовжуємо розбирати відповіді до прикладів на ірраціональні рівняння. Далі наведено 7 прикладів, в яких потрібно знайти корені, області визначення та встановити скільки розв'язків має рівняння.

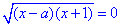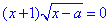Приклад 12.23 Знайти всі значення параметра a, за яких рівняння та рівносильні.

Обчислення: Рівняння є рівносильними, якщо множини їх розв'язків співпадають.
Розв'яжемо кожне з рівнянь, а потім з аналізу множин їх розв'язків встановимо за якого параметра справедливе вказане твердження.
1.
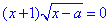
ОДЗ: x-a≥0, звідси x≥a.
Тоді x+1=0 звідси x₁=-1 і x-a=0, звідси x₂=a.

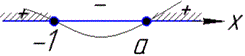
2.
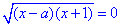
ОДЗ: (x-a)(x+1) ≥0.

Якщо a≥-1, то отримаємо
звідси x∈(-∞;-1] ∪[a;+∞).
Якщо a≤-1, то отримаємо
звідси x∈(-∞;a] ∪[-1;+∞).
Але, якщо a>-1, то рівняння 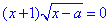матиме єдиний розв'язок x=a (тут x=-1 не задовольняє ОДЗ, оскільки -1-a<0),
а рівняння 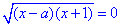матиме два розв'язки x₁=-1, x₂=a і тоді задані рівняння не будуть рівносильними.
При a≤-1 обидва рівняння матимуть два розв'язки x₁=-1, x₂=a (-1-a≥0, тому задовольняє ОДЗ), тобто будуть рівносильними.

Відповідь: a≤-1 – А.

Приклад 12.24 Установити відповідність між заданими рівняннями (1–4) та множинами їх коренів (А–Д).
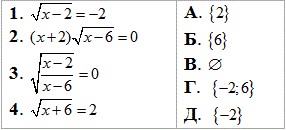Обчислення:Такі завдання розв'язують за однією універсальною схемою:
Спершу встановлюють область визначення, далі обчислення та відкидання зайвих коренів.
1.
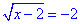
Обмеження на корінь квадратний дасть нам ОДЗ:
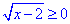, звідси -2≠0.
Отже, рівняння коренів не має, тому x∈∅
1 - В.

2.
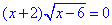
ОДЗ: x-6≥0, звідси x≥6.
Кожен з множників прирівнюємо до нуля та знаходимо розв'язки.
x+2=0, x₁=-2 (не належить ОДЗ x≥6)
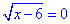, x-6=0, x₂=6.
Отже, рівняння має один корінь x=6
2 - Б.

3.
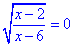
Не забувайте, якщо під коренем маємо дріб то знаменник не повинен перетворюватися в нуль.
Звідси дістаємо систему нерівностей для ОДЗ:

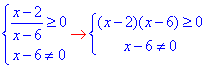
Наносимо точки на числову вісь і з'ясовуємо знаки підстановкою будь-якого числа з проміжку.

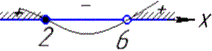
звідси x∈(-∞;2] ∪[6;+∞).
Розв'язуємо рівняння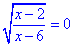
Чисельник може бути рівним нулю x-2=0, звідси x=2.
3 - А.

4.
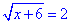
Виписуємо область визначення:
x+6≥0, звідси x≥-6.
Для розкриття ірраціональност обидві сторони підносимо до квадрата та розписуємо

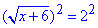
x+6=4,
x=4-6=-2.
4 - Д.

Приклад 12.25 Установити відповідність між заданими рівняннями (1–4) та рівносильними їм рівняннями або системами (А–Д).

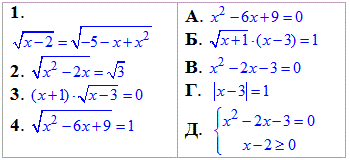
Обчислення: Схема обчислень наступна: деякі обмеження отримаємо з ОДЗ, решта при розкритті коренів коли підносимо до квадрату.
Отримані результати порівнюємо з варіантами А, Б, В,Г, Д ЗНО тестів.
1.
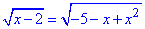
Записуємо область визначення:

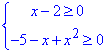
Далі підносимо обидві сторони рівняння до квадрату та спрощуємо

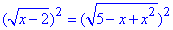
x-2=-5-x+x², x²-2x-3=0
Ірраціональне рівняння рівносильне системі з квадратного рівняння та нерівності

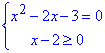
1 - Д.

2. Аналогічні кроки проробляємо для другого та наступних пунктів прикладу

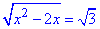
Встановлюємо ОДЗ: x²-2x≥0, x(x-2)≥0,
За необхідності можете множини розв'язків області визначення позначати на числовій осі

звідси x∈(-∞;0] ∪[2;+∞).
Піднесенням до квадрату позбуваємося коренів

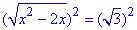
x²-2x=3, x²-2x-3=0,
звідси x₁=-1 і x₂=3.
Обидва корені належать ОДЗ, тому рівняння 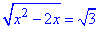і x²-2x-3=0 рівносильні.
2 - В.

3.
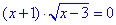
Нерівність для кореневої функції:
x-3≥0, тому x≥3,
x+1=0, x₁=-1 (не належить ОДЗ),
x-3=0, x₂=3.
Отже, рівняння 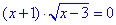має корінь x₂=3.
Розглянемо рівняння: x²-6x+9=0, тобто (x-3)²=0, звідси x=3.
Отож, рівняння 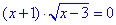і x²-6x+9=0 рівносильні.
3 - А.

4.
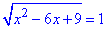
Під коренем маємо квадратичну функцію, вона повинна бути додатною або рівною нулю.
З цього маємо нерівність для ОДЗ:
x²-6x+9≥0, (x-3)²≥0, звідси x∈(-∞;+∞),
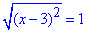, звідси |x-3|=1.
4 - Г.

Приклад 12.26 Установити відповідність між рівняннями (1–4) та областями їх визначення (А–Д).

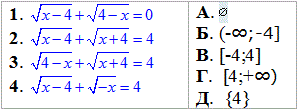
1. Обчислення спрощуються, оскільки нас цікавлять області визначення, а не сам розв'язки ірраціональних рівнянь.

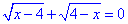
Виписуємо обмеження на кореневі функції:

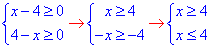
Звідси ОДЗ x=4, або x∈{4}.
1 - Д.

2.
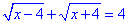
Система нерівностей для області визначення має вигляд:

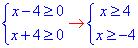
отже x≥4, або x∈[4;+∞).
2 - Г.

3.
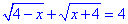
ОДЗ:

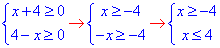
змінна має належати проміжку -4≤x≤4, або x∈[4;4].
3 - В.

4.
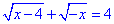
Складемо ОДЗ:

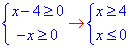
отже x∈∅.
4 - А

Приклад 12.27 Установити відповідність між рівняннями (1–4) та множинами їх коренів (А–Д).

Обчислення: Виконуємо обчислення коренів за схемою:
1. √(-x)=4
Визначаємо ОДЗ: -x≥0, звідси x≤0,
Далі розкриваємо ірраціональність 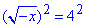та знаходимо розв'язки рівняння
-x=16, отже x=-16, або x∈{-16}.
Не забувайте перевіряти чи корінь входить в ОДЗ.
1 - Г.

2. Аналогічно для всіх решта завдань √x=-4,
ОДЗ: x≥0, -4≤0,
тому рівняння коренів не має, тобто x∈∅.
2 - А.

3.
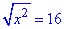
При розкритті кореня квадратного змінну слід взяти за модулем
|x|=16, звідси x₁=16 і x₂=-16, або x∈{-16;16}.
Легко переконатися, що обидва розв'язки перетворюють рівняння в тотожність.
3 - Д.

4. √x -4=0,
ОДЗ: x≥0,
√x =4 ,
,
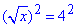отже x=16, або x∈{-16}.
4 - В.

Приклад 12.28 Установити відповідність між рівняннями (1–4) та множинами їх коренів (А–Д).

1. Для непарних степенів кореневих функцій можна опустити визначення області визначення та зразу перейти до розкриття ірраціональності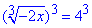
-2x=64, отже x=-32, або x∈{-32}.
1 - В.

2.
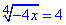
ОДЗ: -4x≥0, звідси x≤0,

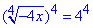
-4x=256, отже x=-64, або x∈{-64}.
2 - Б.

3.
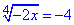
ОДЗ: 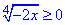, -4 ≤0, тому рівняння коренів не має, тобто x∈∅.
3 - А.

4.
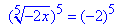
-2x=-32, отже x=16, або x∈{16}.
4 - Д.
На ЗНО тестах можуть зустрітися і важчі завдання, але схема їх обчислень така ж як для розглянутих прикладів.

Приклад 12.29 Установити відповідність між рівняннями (1–4) та кількістю їх коренів (А–Д).
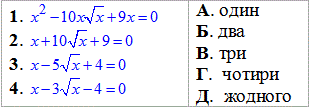Обчислення:
1.
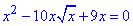
Випишемо ОДЗ: x≥0
Одну зі змінних винесемо за дужки

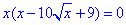
Далі потрібно виконати заміну змінних: √x=t≥0,
тоді x=t², а рівняння набуде вигляду
t²(t²-10t+9)=0,
t²(t-1)(t-9)=0.
звідси t₁=0, t₂=1 і t₃=9.
Повертаючись до заміни x=t², маємо
x₁=0, x₂=1 і x₃=81 (всі три корені належать ОДЗ),
тому задане рівняння має три корені.
1 - В.

2.
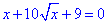
ОДЗ для кореня квадратного: x≥0
Робимо заміну: √x=t≥0, тоді x=t³,
Зводимо до квадратного рівняння
t²+10t+9=0,
(t+1)(t+9)=0.
звідси t₁=-1 і t₂=9 (обидва корені не належать ОДЗ),
тому задане рівняння не має коренів.
2 - Д.

3.
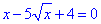
ОДЗ: x≥0,
заміна: √x=t≥0, тоді x=t²,
отримаємо
t²-5t+4=0,
(t-1)(t-4)=0
звідси t1=1 і t²=4.
Повертаючись до заміни x=t², маємо
x₁=1 і x₂=16 (обидва корені належать ОДЗ),
тому задане рівняння має два корені.
3 - Б.

4.
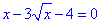
ОДЗ: x≥0
заміна: √x=t≥0, тоді x=t²,
отримаємо
t²-3t-4=0, (t+1)(t-4)=0,
звідси t₁=-1 (не належить ОДЗ) і t₂=4.
Повертаючись до заміни x=t², маємо x=16,
тому задане рівняння має один корінь.
4 - А.

Приклад 12.30 Установити відповідність між рівняннями (1–4) та їх коренями (А–Д).
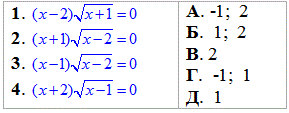Обчислення: Розрахунки для кожного ірраціонального рівняння починаємо з визначення області визначення. Далі розв'язуємо рівняння та відкидаємо зайві корені. При цьому в ході обчислень пропустимо цього разу усі коментарі.
1.
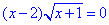
ОДЗ: x+1≥0, звідси x≥-1,
x-2=0, x₁=2 і x+1=0, x₂=-1.
1 - А.

2.
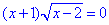
ОДЗ: x-2≥0, звідси x≥2,
x+1=0, x₁=-1 (не належить ОДЗ) і x-2=0, x₂=2.
2 - В.

3.
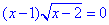
ОДЗ: x-2≥0, звідси x≥2,
x-1=0, x₁=1 і x-2=0, x₂=2.
3 - В.

4.
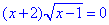
ОДЗ: x-1≥0, звідси x≥1,
x+2=0, x₁=-2 (не належить ОДЗ) і x-1=0, x₂=1.
4 - Д.

Як бачите надважких перетворень тут не виконували, розкриття ірраціональності в більшості завдань звелося до піднесення до квадрату або кубу. Також Ви тепер знаєте як правильно складати систему нерівностей для області визначення.
В наступних уроках розглянемо решту 20 прикладів із ЗНО підготовки.