Продовжуємо аналізувати готові відповіді до ірраціональних нерівностей із ЗНО тестів. Простіші 27 прикладів на складання рівносильних систем нерівностей та розкриття коренів розв'язані на попередніх уроках, без їх перегляду не всі зможуть самостійно розв'язати наведені далі завдання.
Приклад 13.28 Розв'язати нерівність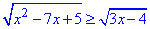 
У відповідь записати найменший цілий розв'язок нерівності.
Обчислення: Маємо нестрогу нерівність з двома коренями квадратними.
Під одним задано квадратний тричлен, корені якого скоріш за все ірраціональні.
Тому для спрощення розрахунків випишемо лише ОДЗ одного з коренів, а після обчислень перевіримо чи в нулях квадратний тричлен приймає потрібний знак (≥0).
Спрощена рівносильна система нерівностей має вигляд
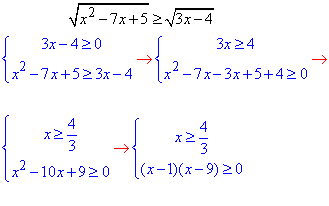
Позначаємо нулі функцій на числовій осі та методом інтервалів визначаємо знаки.
В точці x=9 квадратний тричлен додатний, отже отримані корені уточнювати не потрібно.
В перетині отримали півінтервал x∈ [9; +∞).
Звідси слідує, що число 9 є найменшим цілим розв'язком нерівності.
Відповідь: 9.
Приклад 13.30 Розв'язати нерівність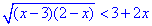 
У відповідь записати добуток усіх цілих розв'язків нерівності.
Обчислення: Підкоренева функція повинна бути ≥0, права сторона при цьому так само приймати значення ≥0.
Ще одну нерівність отримаємо при піднесенні заданої до квадрату.
Сумарно, система рівносильних нерівностей матиме вигляд
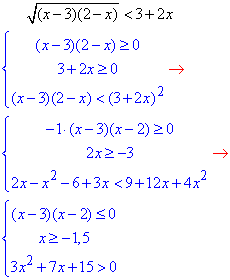
Розв'яжемо квадратне рівняння:
3x^2+7x+15=0,
D=7^2-4•3•15=49-180=-131<0.
Дискримінант від'ємний, отже рівняння дійсних коренів не має.
Звідси слідує, що нерівність 3x^2+7x+15>0
виконується для будь-яких x.
Залишається дві нерівності
{(x-3)(x-2)≤0; x≥-1,5}.
Їх розв'язуємо методом інтервалів, відповідний рисунок наведено далі
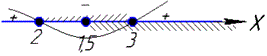В перетині отримаємо проміжок x∈ [1,5; 3].
Тільки два числа 2; 3 є цілими розв'язками заданої нерівності.
Знайдемо їх добуток: 2•3=6.
Відповідь: 6.
Приклад 13.32 Розв'язати нерівність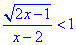 
У відповідь записати суму всіх натуральних чисел, які не є розв'язками нерівності.
Обчислення: Маємо дробово-ірраціональну нерівність. Для її розкриття потрібно область розбити на дві, коли x-2>0 та x-2<0.
Від цього залежатиме знак нерівності, а він необхідний для врахування усіх розв'язків.
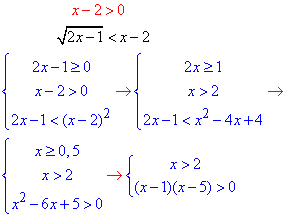
Для від'ємних значень знаменника дробу рівносильна система нерівностей матиме запис
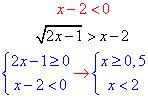
Далі будуємо дві числові осі та методом інтервалів встановлюємо розв'язки нерівностей
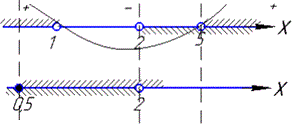З першої системи отримали: x∈ (5; +∞),
з другої системи отримали: x∈ [0,5; 2).
отже розв'язок заданої нерівності (сукупність двох систем):
x∈ [0,5; 2) ∪(5; +∞).
Звідси слідує, що натуральні числа 2; 3; 4; 5 не є розв'язками заданої нерівності.
Знайдемо їх суму: 2+3+4+5=14.
Відповідь: 14.
Приклад 13.33 Розв'язати нерівність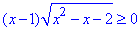 
У відповідь записати найбільше ціле від'ємне число, яке не є розв'язком нерівності.
Обчислення: Складаємо та обчислюємо еквівалентну систему нерівностей
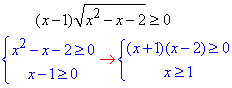
Методом інтервалів визначаємо знаки поза нулями функцій
Розв'язок нерівності : x∈ {-1}∪[2; +∞).
Звідси слідує, що -2 це найбільше ціле від'ємне число, яке не є розв'язком заданої нерівності.
А тепер подумайте чому -2 записуємо у відповіді?
і що потрібно знайти в завданні?
Будьте завжди уважні, адже часом приклад Ви можете обчислити правильно, а відповідь записати невірну.
Тому добре читайте, що від Вас вимагають.
Відповідь: -2.
Приклад 13.34 Розв'язати нерівність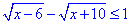 
.
У відповідь записати найменший цілий розв'язок нерівності.
Обчислення: Для розкриття коренів розносимо їх по різні сторони від знаку нерівності та підносимо до квадрату.
Також виписуємо дві умови на ОДЗ коренів квадратних
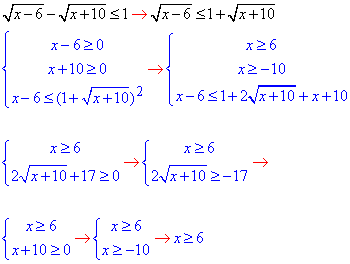
Після перетворень отримали просту нестрогу нерівність
її розв'язок: x∈[6; +∞).
Звідси слідує, що число 6 це найменший цілий розв'язок заданої нерівності.
Відповідь: 6.
Приклад 13.37 Розв'язати нерівність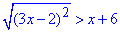 
У відповідь записати суму всіх цілих чисел, які не є розв'язками нерівності.
Обчислення: При розкритті кореня квадратного слід брати вираз за модулем, тому далі розв'язуємо нерівність з модулем
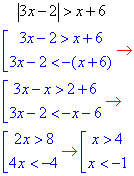
Нанесемо множини розв'язків нерівності з модулем на числову вісь.
З першої нерівності отримали: x∈(-∞;-1),
з другої нерівності отримали: x∈(4;+∞).
Таким чином розв'язок нерівності (сукупність двох нерівностей):
x∈(-∞;-1)∪(4; +∞).
Запам'ятайте, що коли ми маємо справу з модульними нерівностями то розв'язки сумуються, для ірраціональних нерівностей розв'язки є перетином множин, тобто спільними для усіх нерівностей.
Випишемо цілі числа -1; 0; 1; 2; 3; 4 які не є розв'язками заданої нерівності.
Знайдемо їх суму: -1+0+1+2+3+4=9.
Відповідь: 9.
Попереду відібрані найважчі завдання на ірраціональні нерівності, їх можливо навчитися обчислювати, але для цього потрібні добрі знання вище наведеного матеріалу та добра самостійна робота з обчислень рівнянь та нерівностей з коренями.
