Посібник для підготовки до зовнішнього незалежного тестування з математики
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Завантажити (скачати) відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики). Формат: PDF
Зміст: Посібник містить поради щодо проходження ЗНО з математики та взірці тестових завдань.
Усі задачі однієї теми розміщені в порядку складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.
Рік випуску: 2010 р.
Тема 1. Арифметичні приклади та задачі
На попередньому уроці розібрали перших 12 прикладів на знання правил запису чисел, вміння спрощувати вирази. Тут розглянемо задачі на роботу, застосування формул НСД і НСК
Приклад 1.13 Швидкість равлика дорівнює 1/12 м/хв. Яку відстань проповзе равлик за 6 цілих і 1/4 години?
Обчислення: Переведемо час у хвилини, далі за формулою знайдемо відстань
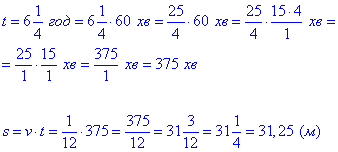
Тут v=1/12 м/хв.
Відповідь: 31,25– Б.
Приклад 1.14 Із 68 жовтих і 85 червоних троянд склали букети, розділивши жовті та червоні троянди в усі букети порівну. Скільки найбільше букетів можна одержати?
Обчислення: Найбільша кількість букетів – це НСД чисел 68 і 85, оскільки усі квіти розділили в букети порівну.
Отож, потрібно знайти НСД (68,85):
68=2•2•17,
85=5•17.
НСД (68,85)=17.
Відповідь: 17 – Г.
Приклад 1.15 Яка найменша кількість метрів тканини може бути в рулоні, щоб його можна було продати без залишку по 6 м, по 8 м, або по 10 м?
Обчислення: Найменша кількість метрів – це НСК чисел 6, 8 і 10, оскільки тканину треба продати без залишку, тобто розділити націло на 6, 8 і 10.
Отож, знайдемо НСК(6;8;10):
6=2•3,8=2•2•2,
10=2•5
НСК(6;8;10)= 2•2•2•3•5=120.
Відповідь: 120 – В.
Приклад 1.16 За три дні зорано 1800 га поля. За перший день зорано 2/9 поля, за другий - 1/6 поля. Скільки гектарів поля було зорано за третій день?
Обчислення: Визначаємо
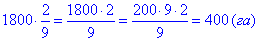- площу поля, що зорано за І день;
- площа поля, що зорано за ІІ день;
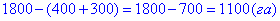- площа поля, що зорана за ІІІ день.
Відповідь: 1100 – А.
Задача 1.17 За перший день турист пройшов 4/9 усього шляху, а за другий – решту – 26 цілих і 2/3 км. поля. Яку відстань пройшов турист за два дні?
Обчислення: Нехай x км – відстань, яку пройшов турист за два дні.
Тоді за І день турист пройшов 4x/9 шляху, а за другий день x-4x/9.
За умовою задачі складемо рівняння та розв'яжемо його:
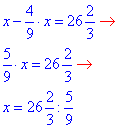
Виконаємо ділення дробів:
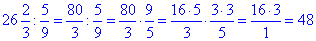
х=48 (км) – відстань, яку пройшов турист за два дні.
Відповідь: 48 км – Д.
Задача 1.18 Басейн наповнюється через першу трубу за 4 години, а через другу – за 6 годин. Яку частину басейну залишиться наповнити після спільної роботи обох труб протягом 2 годин?
Обчислення: Записуємо, що відомо і що потрібно знайти.
1/4 - частина басейну, яку заповнить І труба за 1год;
1/6 - частина басейну, яку заповнить ІІ труба за 1год;
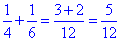- частина басейну, яку наповнять обидві труби за 1 год, працюючи разом.
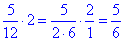- частина басейну, яку наповнять обидві труби за 2 год, працюючи разом.
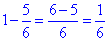- частину басейну залишиться заповнити.
Відповідь: 1/6 – В.
Задача 1.19 Басейн заповнюють водою через першу трубу за a години, а через другу – за b годин.
Через скільки годин можна заповнити басейн при використанні обох труб разом?
Обчислення:Нехай 1/a - частина басейну, яку заповнить І труба за 1год;
1/b - частина басейну, яку заповнить ІІ труба за 1год;
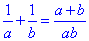- частина басейну, яку наповнять обидві труби за 1 год, працюючи разом.
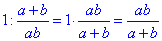год – це час, за який можна заповнити басейн при використанні обох труб разом.
Ще раз проаналізуйте чому так, оскільки багато школярів подібні задачі розв'язують неправильно.
Відповідь: a•b/(a+b) – Г.
Задача 1.20 Майстер виготовляє одну деталь за 5 хв, а через другу, а його учень таку ж деталь – за 9 хв. Працюючи разом вони виготовили 42 деталі. Скільки деталей виготовив майстер?
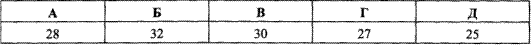
Обчислення: Визначимо, швидкість майстрів за хвилину.
За умовою 1/5 - частина деталі, що виготовляє майстер за 1 хв;
1/9 - частина деталі виготовляє учень за 1хв;
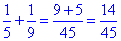- частина деталей, яку виготовлять майстер та учень за 1 хв, працюючи разом.
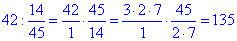хв – час роботи майстра та учня.
135:5=27 дет. – виготовив майстер.
Відповідь: 27 – Г.
Задача 1.21 Добуток двох послідовних парних натуральних чисел дорівнює 728. Знайти суму цих чисел.
Обчислення: Позначимо 2x - перше парне число, тоді 2x+2 - наступне парне число.
За умовою 2x•(2x+2)=728.
Отримали рівняння відносно невідомої, зведемо до квадратного та розв'яжемо його:
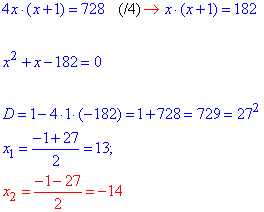
останній корінь не задовольняє умові задачі.
Звідси отримали 2•13=26 і 26+2=28 – задумані числа.
Їх сума: 26+28=54.
Відповідь: 54 – В.
Задача 1.22 В одну місці всі мешканці розмовляють англійською або французькою мовою. Англійською мовою розмовляє 90% всіх мешканців, французькою – 80%. Скільки відсотків мешканців володіє лише однією мовою?
Обчислення: Встановимо, що 100%-90%=10% - мешканців не знають англійської мови;
100%-80%=20% мешканців не знають французької мови.
Звідси, 10%+20%=30% - мешканців володіють лише однією мовою.
Відповідь: 30% – В.
Більше готових відповідей для підготовки до ЗНО тестування в наступній публікації.
