Контрольна робота присвячена розділу диференціювання, його застосуванню при дослідженні функцій на площині та в просторі, пошуку екстремуму функції двох змінних. Наведені розв'язки задач будуть корисні як для студентів стаціонарної форми навчання, так і для заочників.
Завдання 1. Знайти похідні dy/dx заданих функцій.
а)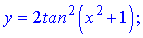 
Розв'язання.Виконуємо диференціювання функцій, використовуючи відомі формули для сладеної функції (степеневої)
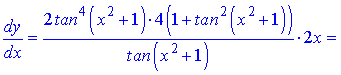
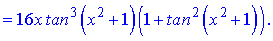
б)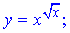 
Розв'язання. Тут можна застосувати логарифмічне диференціювання, а можна обійтися формулами похідної для складеної функції
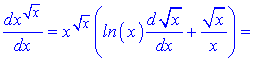
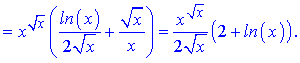
в)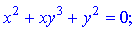 
Розв'язання. Знайдемо значення похідної від неявно заданої функції за правилом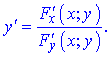
Часткові похідні приймуть значення
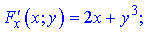
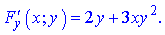
Після підстановки отримаємо таке значення похідної
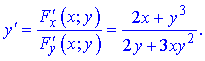
г)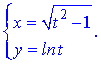 
Розв'язання. Знайдемо похідну параметрично заданої функції за правилом
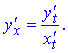
Обчислимо похідні, які входять в залежність
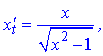
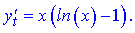
Після спрощення отримаємо такий результат
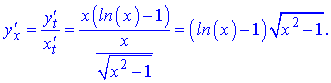
Завдання 2. Доcлідити функцію методами диференціального числення та побудувати її графік
y=x-ln(x+1)
Розв'язання.проходимо всі етапи схеми дослідження функції
1. Область визначення: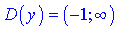 
2. Координати точок перетину графіка з осями координат знаходимо з умови y=0, x=0
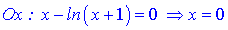
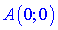
3. Перевірка на парність
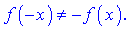
Задана функція ні парна ні непарна, неперіодична.
4. Дослідимо на асимптоти:
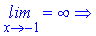
y=-1– вертикальна асимптота.
Рівняння похилої асимптоти має вигляд
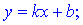
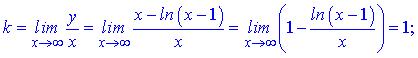
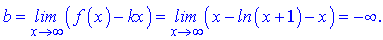
Функціє немає похилої асимптоти.
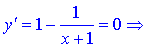
x=0 – точка мінімуму.
5. Графік заданої функції має вигляд:
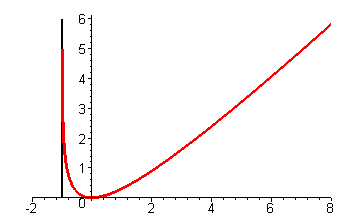
Завдання 3. Із кутів квадратного листа картону розміром 12х12 дм треба вирізати однакові квадрати так, щоб зігнувши лист, одержати коробку найбільшого об'єму. Якою повинна бути сторона вирізаного квадрату ?
Розв'язання. Позначимо через h- сторону відрізаного квадрата. Тоді об'єм знаходимо за формулою
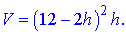
Знайдемо мінімуми і максимуми функції об'єму
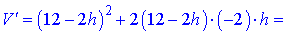
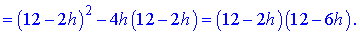
З умови рівності нулю похідної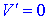 
визначаємо точки ектремуму h=2; h=6.
Підставивши дані значення в функцію об'єму V отримаємо, що при h=2 дм об'єм максимальний і рівний
V=128 дм3.
Отже сторона вирізаного квадрата рівна 2 дм.
Завдання 4. Для функції z=f(x;y) знайти частинні похідні другого порядку
z=arctan(xy2)+y2x.
Розв'язання. Здійснюємо диференціювання функціїї за змінною x та y, після чого знаходимо шукані похідні
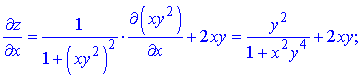
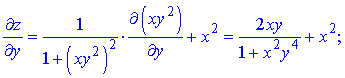
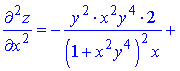
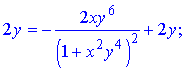
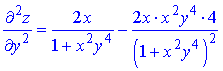
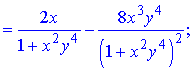
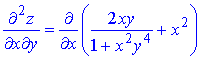
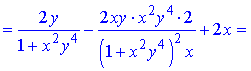
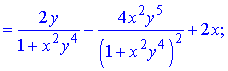
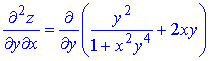
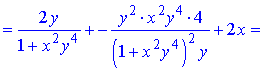
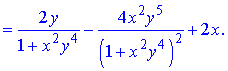
Всі частинні похідні знайдено.
Завдання 5. Дана функція z=f(x;y) і дві точки A(x0;y0) i B(x1;y1).
Обчислити:
1) значення z1 функції в точці B підстановкою координат точки в рівняння поверхні;
2) наближене значення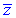
функції в точці B замінивши приріст функції при переході від точки A до точки B диференціалом;
оцінити в процентах відносну похибку при заміні приросту функції її диференціалом;
3) скласти рівняння дотичної площини і нормалі до поверхні z=f(x;y) в точці C(x0;y0;z0)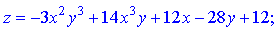
x0=-8;y0=-2
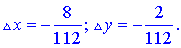
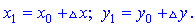
Розв'язання.
1) Знайдемо координати точки B
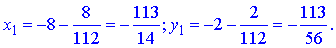
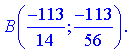
Обчислимо значення функції в цій точці
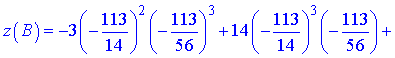
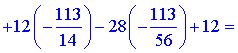
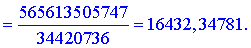
2) Запишемо повний диференціал функції
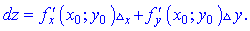
Знайдемо частинні похідні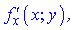 
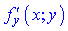
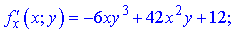
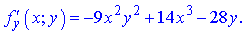
Підставимо початкові точки x0=-8;y0=-2 в знайдені формули
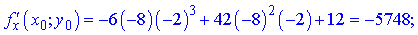
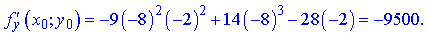
Остаточно диференціал рівний 580,21
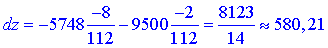
Знайдемо приріст функції dz1 за формулою
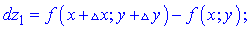
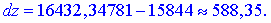
Знайдемо відносну похибку при заміні приросту функції її диференціалом за формулою
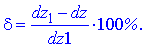
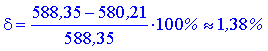
3) Знайдемо значення в точці z(A)
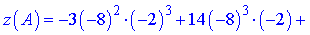
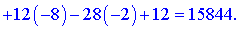
Точка C матиме координати C(-8;-2;15844).
Складемо рівняння дотичної площини за формулою
Продиференціюємо, щоб знайти частинні похідні
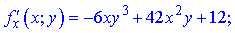
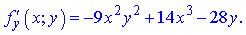
Підставимо знайдене значення C(-8;-2;15844) в отримані залежності
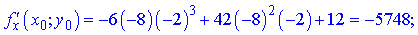
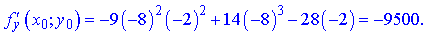
Остаточне рівняння дотичної площини набуде вигляду
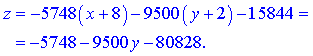
За рівнянням дотичної складаємо рівняння нормалі
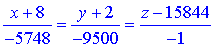
або
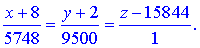
Завдання 6. Знайти найбільше і найменше значення функції z=f(x;y) у замкненій області – трикутнику ABC.
z=x2-4x+y2-32y+12;
A(0;0), B(18;0), C(0;21).
Розв'язання. Знайдемо критичні точки функції, для цього обчислимо частинні похідні та прирівняємо їх до нуля
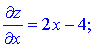
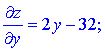
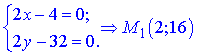
Критична точка M1(2;16) не належить досліджуваній області. А це значить, що функція двох змінних досягає екстремельних значень на сторонах рикутника.
Дослідимо поведінку функції на границях області.
На прямій AB матимемо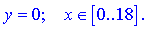 
Функція набуде вигляду
z(x,0)=x2-4x+12.
Дослідимо на екстремуми
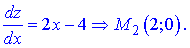
Знайдемо значення функції в цій точці та на краях відрізку
z(A)=12; Z(M2)=8; Z(b)=264.
На прямій AC маємо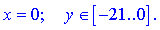 
Функція набуде вигляду
z(0,y)=y2-32y+12.
Дослідимо на екстремуми
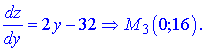
Дана точка не належить проміжку досліджень. Знайдемо значення функції на краях відрізку
z(A)=12; z(C)=1125.
На прямій BC маємо
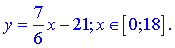
Після підстановки функція z прийме вигляд
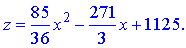
Дослідимо її на екстремуми
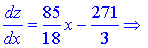
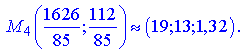
Дана точка не належить досліджуваному проміжку. Значення функції на краях проміжку отримані вище. В розглядуваному трикутнику функція приймає мінімальне і максимальне значення в наступних точках
Подібні контрольні роботи з дослідження функцій, пошуку екстремумів, диференціювання Ви можете зустріти в інтернеті на інших ресурсах. Не лінуйтеся розібратися у їх розв'язанні, це допоможе бути впевненішими при вирішенні контрольних, зрізів, складання іспитів. Також завжди можна знайти свіжі методи вирішення завдань, про які Вам не розповідали на лекціях.
