Контрольні роботи з вищої математики можна зустріти і на інших сайтах, але їх якість і подання не завжди вдалі. Тут Ви отримаєте гарні приклади розв'язання типових при здобутті вищої освіти варіантів контрольних робіт. Їх Ви з легкістю можете застосувати при розв'язуванні подібних завдань, матеріал добре викладено і не вимагає детальних пояснень.
Завдання 1. Скласти рівняння геометричного місця точок площини, якщо відношення їх відстані від точки F(6;-3) до відстані до прямої x=2 дорівнює 14/12.
Розв'язання. Нехай маємо шукану точку F1(x;y) і точку на прямій F2(x;y). Відстань між двома точками обчислюється за формулою
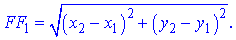
Відстань від точки до прямої є перпендикуляром, тому координати y в даному випадку співпадають
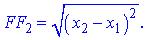
Обчислимо шукані відстані:
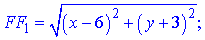
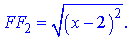
Запишемо відношення даних величин
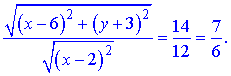
Отримали пропорцію, яка зв'язує потрібні змінні, залишилося її привести до красивого вигляду.
Піднесемо обидві частини до квадрату
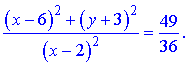
Виконавши ряд перетворень виразимо функцію y через аргумент x
.
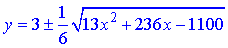В декартовій системі координат дана функція матиме наступний вигляд
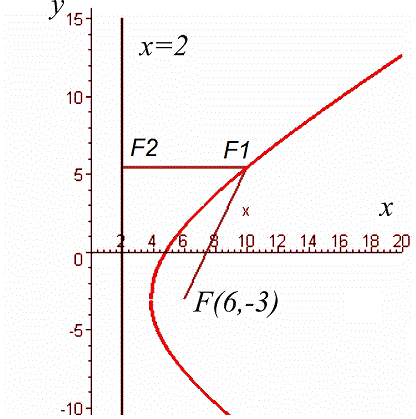
Рівняння після ряду перетворень можна звести до канонічного вигляду
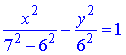
або остаточно
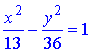
це канонічне рівняння гіперболи.
Розв'язком є права вітка гіперболи з ексцентриситетом е=7/6, директрисою x=2 і фокусом у точці F(6;-3).
Завдання 2. На площині задано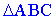 
з вершинами A(2;3), B(4;-1), C(-5;1).
Потрібно знайти:
1) довжину сторони BC;
2) скласти загальне рівняння медіани, висоти та бісектриси кута A;
3) знайти відстань вершини B від медіани;
4) знайти кут між медіаною і висотою (у градусах).
Розв'язання.
1) Довжину сторони знаходимо за формулою
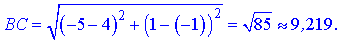
2) Побудуємо рівняння медіани, яка ділить протилежну сторону пополам в точці M(x;y). Знайдемо її координати за формулою середнього арифметичного координат сторони
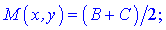
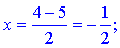
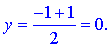
Побудуємо загальне рівняння прямої, що проходить черех точки A(2;3) та M(-0,5;0)
y=A*x+B.
При підстановці точок отримаємо систему із двох рівнянь
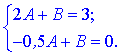
Для відшукання першої невідомої віднімемо від першого рівняння друге
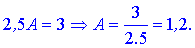
Отримане значення підставляємо в перше рівняння
B=3-2*A=3-2*1,2=0,6.
Рівняння медіани – y=1,2*x+0,6.
Остаточне рівняння медіани, після домноження на 5 і перенесення в ліву сторону, матиме вигляд
6x-5y+3=0.
Складемо загальне рівняння висоти AD. Для цього знайдемо кутовий коефіцієнт сторони BC:
B(4;-1), C(-5;1)
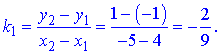
Кутовий коефіцієнт висоти, проведеної з вершини A(2;3) рівний
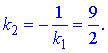
Рівняння висоти, що проходить через точку A має вигляд
y-y1=k1(x-x1);
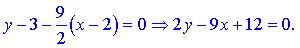
Знайдемо рівняння бісектриси AK. За означенням бісектриса ділить кут пополам, тому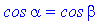 
, де
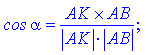
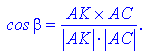
З рівності кутів випливає залежність для визначення рівняння бісектриси
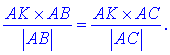
Знайдемо складові рівняння
AB=(4-2; -1-3)=(2;-4),
AC=(-5-2; 1-3)=(-7;-2),
AK=(x-2; y-3),
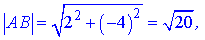
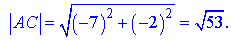
Підставимо знайдені значення у формулу
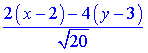
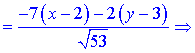
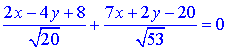
або після спрощень
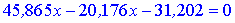
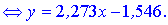
Сам трикутник матиме вигляд
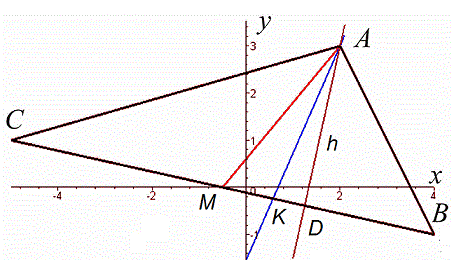
3) Знайдемо відстань від вершини B(4;-1) до медіани 6x-5y+3=0 за форомулою
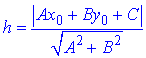
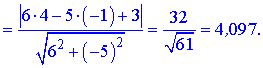
Якщо округлити до десятих, то h=4,1.
4) Маємо дві точки медіани M(-0,5;0), A(2;3) і рівняння висоти 2y-9x+12=0. Виберемо другу точку N з рівняння висоти: при значенні x=0 знаходимо y=-6.
Обчислимо довжини сторін AM(-2,5;-3), AN(-2;-9).
Знайдемо косинус кута між векторами за формулою
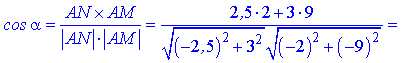
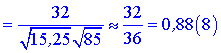
та значення кута в градусах
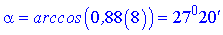
Всі умови завдання виконано.
Завдання 3. Трикутна піраміда задана вершинами
A1(2;3;1), A2(4;2;1), A3(2;1;0), A4(5;2;10).
Потрібно знайти:
1) рівняння грані A1A2A3;
2) рівняння висоти піраміди, яка проходить через вершину A4;
3) довжину цієї висоти;
4) кут між ребром A1A4 і гранню A1A2A3 в градусах;
5) площу грані A1A2A3;
6) oб'єм піраміди.
Розв'язання.
1) Запишемо рівняння площини у вигляді z=A*x+B*y+C.
Оскільки всі три точки належать цій площині то, підставляючи їх по черзі отримаємо систему рівнянь
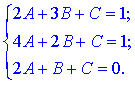
з якої знаходимо невідомі коефіцієнти
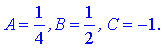
Підставляючи в початкове рівняння, матимемо шукане рівняння грані A1A2A3
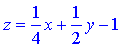або x+2y-4z-4=0.
2) Запишемо рівняння висоти піраміди, яка проходить через вершину A4(5;2;10) на грань
A1A2A3 (x+2y-4z-4=0)
на основі напрямних
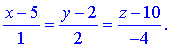
3) Знайдемо висоту, для цього знайдемо довжину сторони
A1A4=(5-2;2-3;10-1)=(3;-1;9).
Враховуючи рівняння грані x+2y-4z-4=0, висоту знайдемо за формулою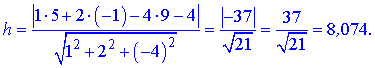
Округлимо до десятих h=8,1.
4) Знайдемо кут між ребром A1A4і гранню A1A2A3 (x+2y-4z-4=0) в градусах.
Запишемо рівняння прямої, що проходить через точки A1(2;3;1), A4(5;2;10)
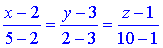
або
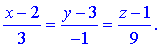
Знайдемо синус кута за формулою
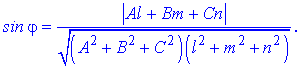
Підставимо значення
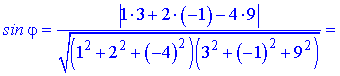
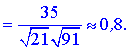
Знаходимо значення кута, яке трохи більше за 53 градуси.
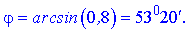
5) Площу грані A1A2A3:
A1(2;3;1), A2(4;2;1), A3(2;1;0)
обчислюємо за формулою половини модулю векторного добутку векторів
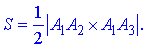
Знайдемо потрібні вектори
A1A2=(4-2;2-3;1-1)=(2;-1;0),
A1A3=(2-2;1-3;0-1)=(0;-2;-1)
та підставимо у формулу площі у скалярній формі
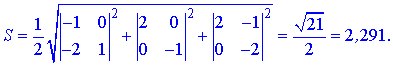
Площа грані рівна 2,3.
6) Обчислимо oб'єм піраміди за формулою
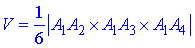
де вектори, що входять рівні
A1A2(2;-1;0), A1A3(0;-2;-1), A1A4(3;-1;9).
Порахувавши визначник
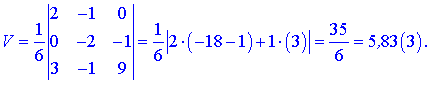
отримаємо, що об'єм піраміди рівний 5,83.
Завдання 4. Дано систему трьох лінійних алгебраїчних рівнянь з трьома невідомими.
Розв'язати систему:
1) за формулами Крамера;
2) засобами матричного числення;
3) методом Гаусса.
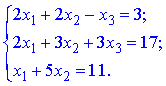
Розв'язання.
1) Застосуємо метод Крамера, для цього обчислюємо визначники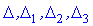 
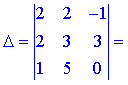
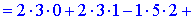
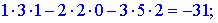
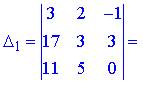
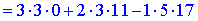
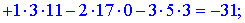
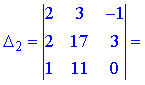
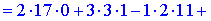
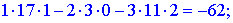
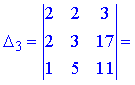
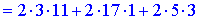
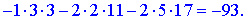
За формулами Крамера знаходимо розв'язки системи рівнянь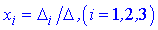 
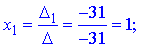
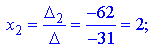
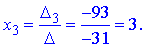
2) Розв'яжемо систему матричним методом. Випишемо матриці та вектори у вигляді
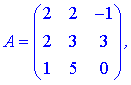
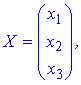
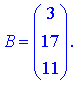
Обчислимо обернену матрицю
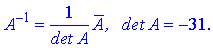
Через визначники другого порядку знаходимо компоненти матриці доповнення
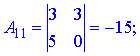
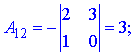
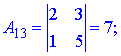
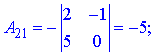
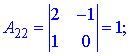
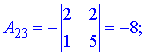
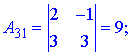
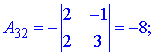
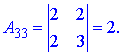
Остаточно, обернена матриця прийме вигляд
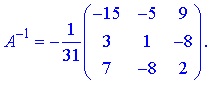
За формулою X=A-1*B знаходимо розв'язок системи рівнянь:
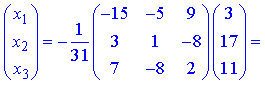
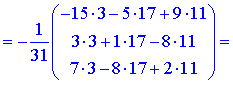
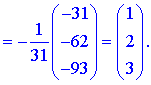
3) Розв'яжемо систему рівнянь методом Гаусса , для цього виписуємо розширену матрицю
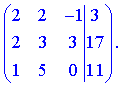
З матрицею виконуємо наступні перетворення: від 2 рівняння віднімемо 2, а від подвоєного 3 віднімемо 1. В результаті отримаємо
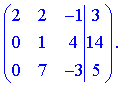
Далі, від другого помноженого на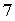 
віднімемо третє
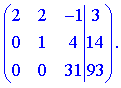
В результаті отримаємо еквівалентну початковій систему рівнянь
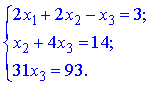
Розв'язуємо дану систему з кінця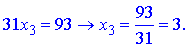 
3 другого рівняння маємо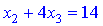 
або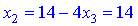 
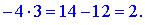
З першого рівняння знаходимо
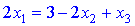
або
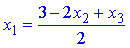
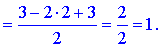
Розв'язок системи рівнянь за Гауссом рівний
x1=1, x2=2, x3=3.
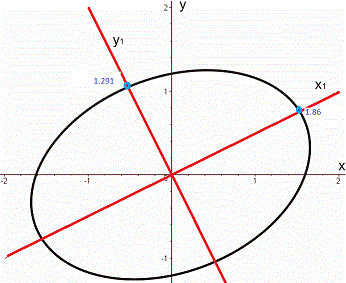
Завдання 5. Звести до канонічного вигляду рівняння кривої другого порядку, використовуючи теорію квадратичних форм. Побудувати стару та нову системи координат і зобразити криву (якщо вона існує).
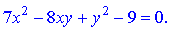
Розв'язання. Виписуємо характеристичне рівняння, яке відповідає заданій кривій
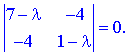
Розв'язавши це рівняння, отримаємо
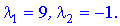
Знайдемо власні вектори, що відповідають власним значенням. Якщо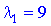 
то маємо таку систему рівнянь для знаходження власного вектора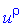 
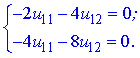
Звідси знаходимо перший вектор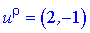 
.
При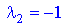
маємо наступну систему рівнянь з якої знаходимо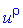 
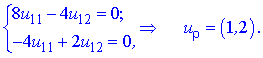
Зводимо власні вектори до одиничних (нормуємо):
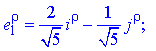
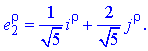
Отже, перетворення координат матиме наступний запис
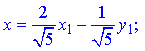
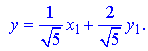
Задане рівняння, після підстановки, стає таким:
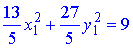
або після спрощення
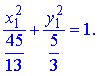
Знайдене канонічне рівняння описує еліпс.
Завдання 6. Обчислити границі (не використовуючи правило Лопіталя):
а)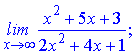 
Розв'язання.При змінній прямуючій до безмежності 
чисельник і знаменник дробу нескінченно великі. Для знаходження границі виразу чисельник і знаменник ділимо на найвищу степінь кожного
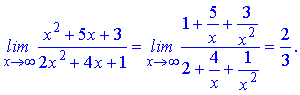
Границя рівна 1/2.
б)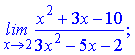 
Розв'язання.Обчислимо границі чисельника і знаменника окремо
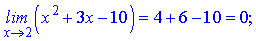
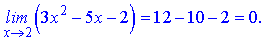
Границі чисельника і знаменника прямують до нуля при при змінній 
, а отже отримуємо невизначеність типу нуль поділити на нуль {0/0}.
Теорему про границю частки напряму застосовувати не можна, потрібно знаменник і чисельник скоротити на спільний множник, який прямує до нуля
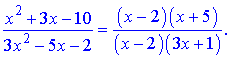
Тоді границя прийме значення
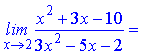
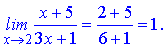
в)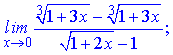 
Розв'язання.Границю дробової ірраціональної функції знайдемо, записавши степеневий розклад коренів в чисельнику та знаменнику при змінній прямуючій до нуля 
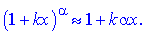
Застосовуючи даний розклад в ряд, знаходимо границю
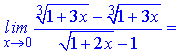
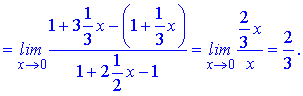
г)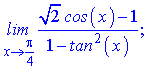 
Розв'язання.Легко переконатися, що при підстановці у границі межі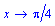 
чисельник і знаменник прямують до нуля. Для знаходження границі розкладемо функції cos(x), tan2(x) по степенях змінної в оолі точки x=Pi/4
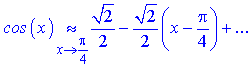
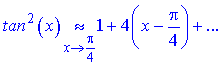
Підставимо отримані значення в границю та спростимо
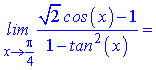
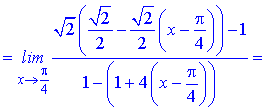
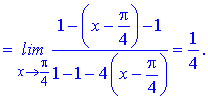
д)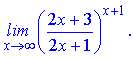 
Розв'язання. Зведемо дріб в дужках до формули другої чудової границі
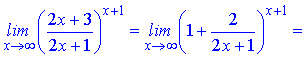
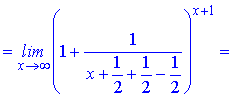
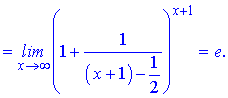
в результаті обчислень отримаємо експоненту.
