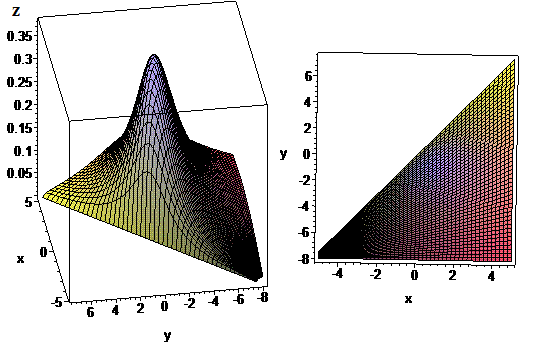До Вашої уваги готова контрольна робота на аналіз функції двох змінних на екстремум, обчислення частинних похідних, знаходження дотичної та нормалі до поверхні. Всі приклади взяті з реальної контрольної, яку можливо доведеться вирішувати комусь із Вас. Перегляньте та запам'ятайте методику обчислення такого роду завдань.
Приклад 1. Знайти область визначення вказаних функцій:
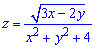
Розв'язання: Маємо дробову функцію, крім цього в чисельнику корінь квадратний. Областю визначення (ОДЗ) будуть всі точки декартової площини в яких знаменник не перетворюється в нуль+підкореневий вираз приймає невід'ємні значення. Разом ці дві умови складають систему з двох рівнянь
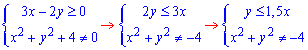
Знаменник завжди більший нуля і лише чисельник обмежує область визначення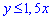 
.
Таким чином область визначення заданої функції є півплощина, яка знаходиться нижче прямої 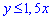, включаючи саму пряму також.
Фрагмент просторового графіку ф-ї 2 змінних та її області визначення наведено нижче
Для побудови використано математичний пакет Maple, про його переваги над іншими пакетами на сайті чимало інформації.
Все, що потрібно - це ввести наступний код
> restart;with(plots):
> z:=sqrt(3*x-2*y)/(x^2+y^2+4);
> plot3d(z,x=-5..5,y=-8..1.5*x);
Покрутивши графіком, можна отримати наступні форми
Приклад 2. Знайти частинні похідні і частинні диференціали по кожній змінній від функції:
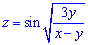Розв'язання:Завдання не з легких, оскільки задано складено функцію. Маємо синус від кореневої функції від дробу. Тож беручи похідну за змінною x,y будьте уважні
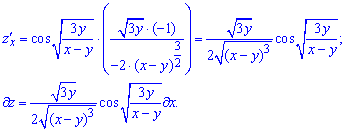
Після знаходження частинних похідних диференціал скласти не проблема.
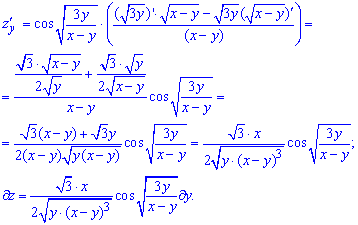
Уважно гляньте, як знайти похідну складеної функції.
Приклад 3. Обчислити значення частинних похідних f'x(M0), f'y(M0), f'z(M0) для заданих функцій f(x;y;z) в точці M0(x0; y0, z0) з точністю до двох знаків після коми: f(x;y;z)=xz/(x-y), M0(3;1;1).
Розв'язання:Завдання не важке, обчислюємо частинні похідні за змінними x,y, далі в формули підставляємо початкову точку. В результаті цього отримаємо
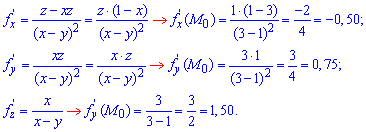
Приклад 4. Знайти повний диференціал функції: z=x2y-4x3y3+2Pi.
Розв'язання:Спершу знаходимо частинні похідні функції z(x,y) за змінною x,y
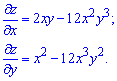
Далі підставляємо їх в формулу повного диференціалу функції
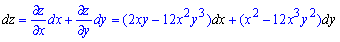
Приклад 5. Обчислити значення похідної складеної функції u=u(x,y), де x=x(t), y=y(t), при t=t0 з точністю до двох знаків після коми: u=ln(e2x+e-2y), x=t2, y=t4, t0=1.
Розв'язання:Подібні завдання Ви скоріш за все вирішували, тому теорії тут розписувати не будемо. Спершу обчислюємо частинні похідні по x, y,t відповідно:
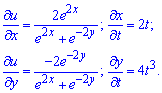
Далі підставляємо їх в формулу похідної складеної функції:
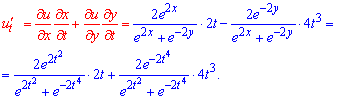
Функція за умовою досить поста, тож маємо мінімум перетворень.
Останнім кроком підставляємо значення параметра в похідну і округлюємо відповідь до двох значень після коми.
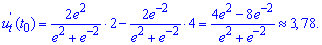
Похідна складеної функції в точці t0=1 приблизно рівна 3,78.
Приклад 6. Обчислити значення частинних похідних функції z(x,y) заданої неявно, в даній точці M0(x0; y0, z0) з точністю до двох знаків після коми: x3-z3+3xyz=27, M0(3; 1, 13).
Розв'язання: Нехай маємо функцію, що задана неявно:
F(x;y;z)=x3-z3+3xyz-27, тоді її частинні похідні в точці M0 приймають значення
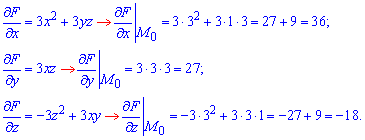
Ось і всі обчислення до даного завдання. Ніколи не лякайтеся умов, а лише вдумливо читайте, що від Вас вимагають.
Приклад 7. Записати рівняння дотичної площини і нормалі до поверхні S в точці : M0(x0; y0, z0):
z=2x2-3y2+4x-2y+10, M0(-1;1, 3).
Розв'язання: Нехай маємо рівняння поверхні:
F(x;y;z)=2x2-3y2+4x-2y-z+10
Обчислимо часткові похідні функції в заданій точці
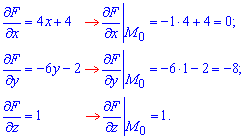
Далі складаємо рівняння дотичної площини:
0(x+1)-8(y-1)+1(z-3)=0 або 8y-z-5=0.
Запишемо рівняння нормалі до поверхні:
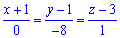
Приклад 8. Знайти другі частинні похідні функції. Переконатися в тому, що мішані похідні рівні між собою z''xy=z''yx:
z=arcsin(4x+2y).
Розв'язання:Знайдемо частинні похідні за обома змінними
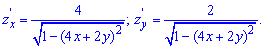
Обчислимо другі частинні похідні заданої функції
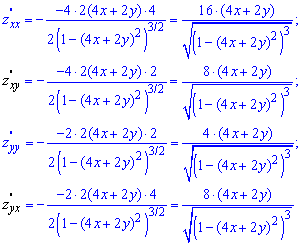
З форму бачимо, що умова рівності мішаних похідних виконується
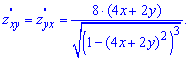
Приклад 9. Перевірити, чи задовольняє вказаному диференціальному рівнянню функція u=u(x,y):
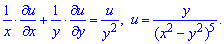
Розв'язання: Знайдемо часткові похідні функції за змінними x,y:
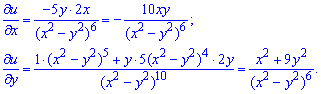
Підставимо знайдені часткові похідні функції у початкове рівняння та спростимо:
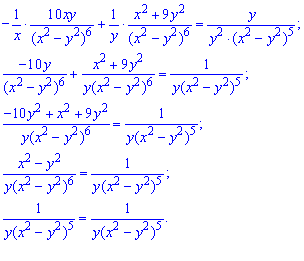
Отримали тотожність, тому задана функція задовольняє вказаному рівнянню.
Приклад 10. Дослідити на екстремум такі функції: z=(x-5)2+y2+1.
Розв'язання: Розділимо дослідження функції двох змінних на екстремум у 3 необхідних етапи:
1) Знайдемо критичні точки - для цього обчислимо часткові похідні
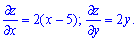
2) З умови рівності часткових похідних нулю складаємо систему рівнянь
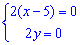
з якої визначаємо точки підозрілі на екстремум звідси x=5; y=0.
3) знайдемо похідну другого порядку в критичній точці A(5;0) :
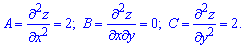
Далі встановимо характер особливості
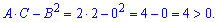
Значення більше нуля, отже в точці (5;0) функція двох змінних має мінімум, а саме zmin=1.
Фрагмент коду в Maple та графік функції в околі точки екстремуму наведено нижче
> restart;with(plots):
> z:=(x-5)^2+y^2+1;
> plot3d(z, x=6..4,y=-1..1);
Також в мейплі без проблем можна знаходити частинні похідні (функція >diff(z,x);) та виконувати весь наведений аналіз.
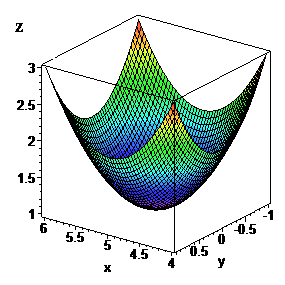
Залишайтеся з нами, на сайті Вас чекає багато готових контрольних робіт з вищої математики та просто якісно підготовлених відповідей до завдань.
